Счетчики

Конечный автомат, циклически переходящий из одного состояния в другое под действием сигналов, подаваемый на один информационный вход, называются счетчиком.

Количество входных переключающих сигналов, которое надо подавать на вход счетчика для того, чтобы счетчик вернулся в исходное состояние, называется коэффициентом пересчета счетчика и обозначается буквой “К”.

На структурных схемах счетчики обозначаются следующим образом:

Микрооперации имеют следующий смысл:

y₁ : Cr := Cr + 1

y₂ : Cr := 0

y₃ : РгА := Cr

N – количество разрядов

(триггеров) в счетчике.

Различают следующие типы счетчиков:

1. счетчики с последовательным переносом, в которых входной переключающий сигнал непосредственно воздействует лишь на первый триггер и каждый триггер вырабатывает переключающий сигнал для следующего соседнего триггера;

2. счетчики с параллельным переносом, в которых входной переключающий сигнал непосредственно воздействует на все триггеры счетчика и каждый триггер вырабатывает для всех последующих лишь сигналы управления;

3. счетчики с последовательно-параллельным переносом, в которых триггеры разбиты на группы, причем внутри группы соединения выполнены как в схеме с параллельным переносом, а между группами – как в схеме с последовательным переносом.

Также как для любых конечных автоматов, состояние счетчика в любой момент времени определяется кодом Q, который зафиксирован на его триггерах. Исходное (начальное) состояние обозначается через Q. Состояние, в котором находиться счетчик после n – го входного переключающего сигнала, обозначается через Qⁿ. Задать правила работы счетчика – значит определить тем или иным способом функцию приn = 0, 1, 2,…, k, где n – номер входного переключающего сигнала. Очевидно, что при любомn.

Правила работы N – разрядного двоичного суммирующего счетчика с любой организацией переноса имеют вид:

При малых N правила работы задаются в виде таблицы переключения счетчика. Например, при N = 3 и Q = 000, эта таблица имеет вид:

Qn
n	Q3n	Q2n	Q1n
0	0	0	0
1	0	0	1
2	0	1	0
3	0	1	1
4	1	0	0
5	1	0	1
6	1	1	0
7	1	1	1

Синтез счетчика удобно выполнять, исходя из таблицы переключения, предполагая, что все триггеры счетчика одинаковы. Действительно, из столбца , соответствующего младшему разряду зафиксированного на счетчике числа, видно, что первый триггер счетчика – это Т – триггер, т.к. каждый входной сигнал переводят этот триггер в новое состояние, следовательно, и остальные триггеры – Т-триггеры.

Будем синтезировать счетчик с последовательным переносом, в котором каждый триггер вырабатывает переключающий сигнал для следующего триггера. Из таблицы переключения видно, что i – й триггер переключается тогда, когда (i - 1) – й триггер переходит из состояния «1» в состояние «0». Поэтому инверсный выход (i - 1) – го триггера необходимо соединить с Т – входом i - го триггера.

Схема такого счетчика имеет вид:

Аналогично можно построить схему суммирующего счетчика с последовательным переносом на D – триггерах, каждый из которых работает как Т – триггер. Такая схема имеет вид:

Правила работы N – разрядного двоичного вычитающего счетчика с любой организацией переноса имеют вид:

Рассуждая так же, как и в предыдущем случае, можно получить следующие схемы вычитающих счетчиков с последовательным переносом:

Если в любой из рассмотренных счетчиков ввести схему коммутации между выходом i – го триггера и входом (i + 1) – го триггера, на которую подать дополнительный управляющий сигнал F, то получим схему реверсивного счетчика с последовательным переносом.

Пусть при Fⁿ = 0 реверсивный счетчик работает как суммирующий, а при Fⁿ = 1 – как вычитающий, тогда правила работы схемы коммутации на первый взгляд могли бы быть следующими:

, где T_i – сигнал на Т – входе.

Однако изменение значения сигнала управления F может вызвать переключение счетчика при неизменном входном сигнале. С целью исключения неправильных переключений можно принять, что сигнал F изменяется только при  = 0, и следующим образом изменить правила работы схемы коммутации:

Эти правила определяют функцию возбуждения , которой соответствует следующая таблица:

A	F	Qi-1	Ti
0	0	0	0
0 запрет	0	1	0
0	1	0	0
0	1	1	0
1	0 суммирование	0	1
1 счет	0	1	0
1	1 вычитание	0	0
1	1	1	1

Из таблицы получаем:

Схема трехразрядного реверсивного счетчика с последовательным переносом будет иметь вид:

Важным параметром счетчиков является разрешающее время. Разрешающим временем t_раз счетчика называется минимальный временной интервал между двумя входными переключающими сигналами, при котором счетчик еще правильно функционирует. Принято, что счетчик правильно функционирует, если в каждом из состояний, определяемых правилами работы, он находиться в течение времени , где_min – заданная величина, когда производиться считывание содержимого счетчика. Для разрешающего времени счетчиков с последовательным переносом t_раз.п. нетрудно получить следующую формулу:

где t_раз.тр. – разрешающее время первого триггера;

t_зад.тр. – время задержки триггера;

t_зад.ск. – время задержки схемы коммутации; (для суммирующего и вычитающего счетчиков t_зад.ск. = 0)

Для ускорения процесса счета в счетчике необходимо, чтобы изменение состояний отдельных разрядов происходило не последовательно, а непосредственно вслед за приходом очередного счетного сигнала. Будем синтезировать счетчик на Т – триггерах. Для первого триггера суммирующего счетчика справедлива следующая таблица переключения:

n	Q1n	Q1n+1
0	0	0
0	1	1
1	0	1
1	1	0

Отсюда следует, что :

Для второго триггера счетчика таблица переключений будет такой:

n	Q1n	Q2n	Q2n+1
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

Перенесем эту таблицу на карту Карно:

Отсюда получаем :

Аналогично получим соответствующее выражение для третьего триггера:

n	Q1n	Q2n	Q3n	Q3n+1
0	0	0	0	0
0	0	0	1	1
0	0	1	0	0
0	0	1	1	1
0	1	0	0	0
0	1	0	1	1
0	1	1	0	0
0	1	1	1	1
1	0	0	0	0
1	0	0	1	1
1	0	1	0	0
1	0	1	1	1
1	1	0	0	0
1	1	0	1	1
1	1	1	0	1
1	1	1	1	0

В общем случае для i– го разряда счетчика можно записать:

()

Последнее выражение позволяет построить счетчик с параллельным переносом. Схема такого счетчика имеет вид (на синхронных Т - триггерах):

Разрядность счетчика с параллельным переносом ограничивается возможностями логических элементов: коэффициентом разветвления триггеров и коэффициентом объединения схем И. В тех случаях, когда указанные ограничения не позволяют построить схему счетчика с заданным числом разрядов, счетчик разбивается на группы и синтезируется счетчик с последовательно-параллельным переносом (внутри группы перенос параллельный, а между группами - последовательный). Иногда строят счетчик и с параллельно-параллельным переносом (внутри группы перенос параллельный и между группами параллельный). Однако такой счетчик требует больших аппаратурных затрат.

Разрешающее время суммирующего счетчика с последовательно-параллельным переносом определяется так:

где t_раз.тр. – разрешающее время первого триггера;

t_зад.тр. – время задержки триггера;

- заданная минимальная длительность каждого состояния счетчика;

p– количество групп триггеров;

При p= 1получаем разрешающее время для счетчика с параллельным переносом.

Уравнение (  ) позволяет получить схему суммирующего счетчика со сквозным переносом. Такой счетчик может быть построен на синхронных Т – триггерах. При этом на синхронизирующий вход этих триггеров заводиться счетный сигнал₀, а на счетные входы – сигналы₁,₂, ….

Схема четырехразрядного счетчика со сквозным переносомимеет вид:

При одном и том же числе разрядов Nсчетчики с последовательным переносом имеют самую простую схему и наибольшее разрешающее время (т.е. являются наиболее низкочастотными), а счетчики с параллельным переносом – самую сложную схему и наименьшее разрешающее время (т.е. являются наиболее высокочастотными). Счетчики с последовательно-параллельным переносом занимают промежуточное положение как по сложности схем, так и по значению разрешающего времени.

Двоичные N– разрядные счетчики позволяют осуществлять деление частоты следования сигналов счета с коэффициентом пересчета равным 2^N. На их основе могут быть также построены делители частоты с произвольным коэффициентом пересчета. Такие делители частоты строятся обычно на основе двоичных счетчиков с последовательным переносом.

Пусть требуется построить счетчик с коэффициентом пересчета K= 5. Очевидно, что минимальное количество триггеровmв этой схеме должно удовлетворять условию:

2^m  k > 2^{m – 1}

При k= 5 должно бытьm= 3.

Построим таблицу переключений трехразрядного суммирующего счетчика, причем за исходное состояние возьмем код числа:

Q₀ = 2^m – k = 2³ – 5 = 8 – 5 = 3

Для реализации первых шести строк таблицы может быть использован любой суммирующий счетчик.

N	Qn3	Qn2	Qn1
0	0	1	1
1	1	0	0
2	1	0	1
3	1	1	0
4	1	1	1
5	0	0	0
OC	0	1	1

Переход к шестой строке, отмеченный буквами ОС (обратная связь) отличается от обычных переходов и требует использования триггеров с дополнительным установочным входами.

Пусть в схеме счетчика используются DRS– триггеры. Тогда для перехода в состояние 001 достаточно подать сигнал «0» на установочные входыSпервого и второго триггеров. Этот сигнал – сигнал обратной связи – возникает при переключение счетчика из состояния 111 в состояние 000. Т.о., состояние 000 является промежуточным в том смысле, что счетчик находиться в этом состояние только пока вырабатывается сигнал обратной связи. Код 000 в качестве промежуточного выбран не случайно. Дело в том, что использование промежуточного состояния 000 позволяет в качестве признака необходимости выработки сигнала обратной связи использовать переключение последнего триггера счетчика из состояния «1» в «0».

При использование любого другого промежуточного кода для выработки сигнала обратной связи потребуется дешифратор.

Поскольку сигнал «0» на установочных входах не допускает переключения триггера по входу С, его нельзя подавать непосредственно с выхода последнего триггера – при таком соединении счетчик не будет переключаться после перехода в состояние 011. Поэтому сигнал обратной связи должен быть тем или иным способом укорочен так, чтобы к моменту поступления очередного сигнала ₀сигнал обратной связи уже закончился.

Для укорачивания сигнала обратной связи можно использовать дополнительный DRS– триггер, который устанавливается в состояние «0» при₀= 0, т.е. в промежутке времени между счетными импульсами. Схема счетчика с К = 5 и с дополнительным триггером, имеет вид:

Формировать короткие импульсы обратной связи можно также с помощью элементов И–НЕ. Схема счетчика с таким формирователем имеет вид: 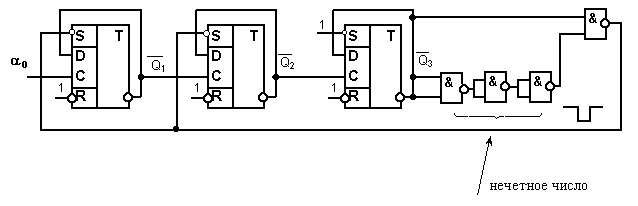Здесь импульс формирователя заканчивается до поступления нового входного сигнала₀= 1.

На основание рассмотренных примеров можно сформулировать общие правила синтеза счетчиков с последовательным переносом на DRS– триггер по заданному коэффициенту пересчета К:

1. Определяется количество триггеров mиз условия2^m  k > 2^{m – 1}.

2. Определяются триггеры, на установочные входы Sкоторых подается сигнал обратной связи. Для этого рассчитывается двоичный код числа, соответствующего начальному состоянию счетчика:Q₀ = 2^m – k. Номера разрядов этого кода, в которых записана единица, совпадает с номером триггера на которые подается сигнал обратной связи.

3. Выбирается схема формирователя и сигнал обратной связи подается на установочные входы Sтриггеров.

Если счетчик должен иметь заданный коэффициент пересчета, начиная с первого цикла работы, то схему необходимо дополнить цепью установки начального состояния Q₀(в рассмотренных примерах – код 011).

Во всех рассмотренных схемах счетчиков число представляется двоичным кодом. На практике часто возникает необходимость представлять число унитарным кодом, в котором только на одной позиции фиксируется «1», а на всех остальных – «0». Здесь каждому числу ставиться в соответствие положение «1» на разрядной сетке. Например:

n	Q1n	Q2n	Q3n	Q4n	Q5n
0	0	0	0	0	0
1	1	0	0	0	0
2	0	1	0	0	0
3	0	0	1	0	0

F– установка исходного состояния

Итак, вернемся к счетчику с унитарным кодированием числа. Если рассмотренный нами ранее последовательный регистр наDRS – триггерах замкнуть в кольцо, соединив информационный вход и выход, в качестве начального состояния выбрать код 001 и на входы С всех триггеров подавать входные сигналы ₀, то получим схему так называемого кольцевого счетчика:

Таблица переключений такого счетчика имеет вид:

N	Q3n	Q2n	Q1n
0	0	0	1
1	0	1	0
2	1	0	0
3	0	0	1

Очевидно, что коэффициент пересчета К = 3.

Достоинства кольцевого счетчика сводятся к следующему:

1. каждому состоянию счетчика соответствует унитарный код;

2. соединения в схеме весьма просты при любом коэффициенте пересчета;

3. разрешающее время мало – такое же как и в схеме с параллельным переносе.

Основной недостаток схемы заключается в том, что при одном и том же коэффициенте пересчета она содержит больше триггеров, чем счетчики, рассмотренные раннее. Кроме того, при одиночном сбое (появлении на триггерах кода, отличающегося от унитарного) изменяется коэффициент пересчета схемы. Последний недостаток можно устранить путем включения дополнительной защитной комбинационной схемы:

Здесь сигналы с инверсным выходом первого и второго триггеров подаются на входы дополнительной схемы И, выход которой подключается ко входуD первого триггера, при этом выход Q₃ остается свободным. После сбоя заданный коэффициент пересчета восстанавливается не более чем за два входных переключающих сигнала.

Разновидность кольцевых счетчиков являются счетчики Джонсона. Они строятся аналогично, но цепочка из n триггеров имеет не n, а 2n состояний. Единственное различие между кольцевым счетчиком и счетчиком Джонсона состоит в том, что вход регистра сдвига соединен не с выходом Q последнего триггера, а с выходом . Это, естественно, приводит к различию в действии обоих устройств:

1. Вместо “перескакивания” с каждым тактовым импульсом единицы из триггера в триггер здесь единичное состояние принимает очередной триггер, и так – в течение первых n импульсов.

2. По достижении единичного состояния всеми триггерами счетчика Джонсона в течение следующих n тактовых импульсов будет происходить “заполнение” триггеров нулями. По достижение всеми триггерами нулевого состояния описанный цикл работы счетчика повторяется.

На практике часто возникает необходимость синтезировать счетчик с наибольшим для данной системы элементов, быстродействием. Принцип построения счетчика, имеющего минимальное разрешающее время, заключается в том, что каждый из m триггеров должен переключаться возможно реже. Отсюда следует, что каждый триггер нужно переключать один раз за m входных переключающих сигналов и вся схема возвращается в исходное состояние за 2m входных переключающих сигналов, т.е. k = 2m. Для этой цели пригодны рефлексные коды, как и код Грея имеющие между соседними комбинациями единичные расстояния по Хэммингу.

В соответствии с рефлексным кодом таблица переключений трех триггеров имеет вид:

n	Q3n	Q2n	Q1n
0	0	0	0
1	0	0	1
2	0	1	1
3	1	1	1
4	1	1	0
5	1	0	0
6	0	0	0

Если в исходном состоянии каждый триггер находился в положении “0”, то по мере поступления входных переключающих сигналов все триггеры сначала переключаются в положение “1”, а затем один за другим возвращаются в положение “0”.

Из таблицы переключений находим, что:

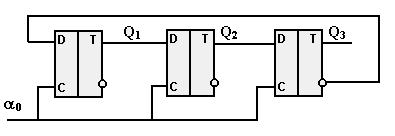
Отсюда следует, что при использовании D – триггеров, схема счетчика будет иметь вид:

При произвольном m схема строиться точно так же: все m триггеров с первого до последнего соединяются как в последовательном регистре, и инверсным выход m – го триггера подключается к D – входу первого триггера. Входные сигналы подаются одновременно на все С – входы триггеров.

Разрешающее время:

,

где t_раз.тр. – разрешающее время первого триггера;

t_зад.тр. – время задержки триггера;

- заданная минимальная длительность каждого состояния счетчика;

p– число разрядов;

Если t_раз.тр.>t_зад.тр.+, то очевидно, что быстродействие этого счетчика выше, чем в схеме с параллельным переносом. Можно утверждать, что не существует схемы счетчика на триггерах, позволяющей получить меньшее разрешающее время, чем в рассмотренной схеме.

В этой схеме, так же как и в схеме кольцевого счетчика, вследствие одиночного сбоя может измениться коэффициент пересчета. Устраняется этот недостаток аналогично, путем подключения комбинационной схемы защиты, которая автоматически восстанавливает заданный коэффициент пересчета.