VII Кореляційний аналіз детермінованих сигналів Лекція 7 (21). Автокореляція і взаємна кореляція сигналів

1. Вступні зауваження.

2. Автокореляційна функція сигналу та її властивості.

3. Зв'язок між енергетичним спектром сигналу і його автокореляційною функцією.

4. Взаємна кореляційна функція та її зв’язок зі взаємною спектральною щільністю.

1. На перших етапах розвитку ТКС питання вибору найкращого в якому-небудь відношенні сигналу не було критичним: повідомлення, що передавались, були простими, а реалізація складних сигналів (їх формування і обробки) була технічно складною. В сучасних ТКС вибір застосовуваних сигналів зумовлений насамперед не технічними зручностями їх формування і обробки, а можливістю на базі цих сигналів оптимально, з максимальною ефективністю, розв’язувати завдання, передбачені при проектуванні системи.

Наприклад, в імпульсному радарі інформація про об’єкт вимірювання дальності закладена у величині 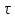– задержці сигналу прийнятого (ехо-сигналу ) відносно зондуючого сигналу. Форма зондуючого сигналу і прийнятого сигналу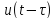однакова при будь–яких задержках. Структурна схема пристрою обробки радіолокаційних сигналів, призначеного для вимірювання дальності

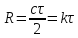
до цілі, показана на рис. 7.1. На схемі ,,…– елементи задержки зондуючого сигналу. Задержані сигнали разом із прийнятим сигналом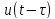надходять на відповідні пристрої порівняння (Пр Пор). Сигнал на виході Пр Пор з'являється лише за умов, що обидва вхідні коливання є “копіями” один одного. Знаючи номер того каналу (1, 2,…), у якому відбувається вказана подія, можна визначити задержку, а відтак і дальність до цілі. Такий вимірювач працюватиме тим точніше, чим у більшій мірі відрізняються між собою сигнал і його “копія”, зміщена у часі. І дійсно, якщо ця відмінність є невеликою, то можна, наприклад, очікувати неоднозначність відліку, коли сигнали з’являтимуться одночасно на виході кількох суміжних пристроїв порівняння.

Рисунок 7.1

Постає завдання кількісно визначити ступінь відмінності сигналу і його зміщеної копії. Це завдання вирішуєкореляційний аналіз сигналів. Саме він дозволяє давати оцінку швидкості зміни і тривалості сигналу, не розкладаючи його на гармоніки в спектр, тобто не виходячи із часової області.

2. Для кількісного визначення ступеня відмінності сигналу від сигналувводять автокореляційну функцію, (АКФ), яка дорівнює скалярному добуткові цих двох сигналів:

(7.1)

Властивості АКФ.

1. При АКФ стає рівною енергії сигналу:

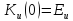(7.2)

2. АКФ є парною функцією:

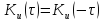(7.3)

3. При будь–якому значенню часового зсуву модуль АКФ не перевищує енергії сигналу:

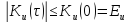(7.4)

Доведенням цього відношення є нерівність Коші-Буняковського

Із властивостей АКФ випливає, що ця функція репрезентується симетричною кривою з центральним максимумом, завжди додатним. При цьому в залежності від виду сигналу АКФ може мати як монотонно спадний, так і коливальний характер.

Приклади АКФ.

1. АКФ відеоімпульсу

(7.5)

Рисунок 7.1

2. АКФ радіоімпульсу

(7.6)

Рисунок 7.2

3. АКФ серії з трьох відеоімпульсів.

Рисунок 7.3

А як визначати АКФ необмежено протяжного у часі сигналу? Адже інтеграл у (7.1) не буде сходитися. Задля уникнення несходимості інтегралу застосовується модифікований вираз для АКФ де вона визначається як середнє значення скалярного добутку сигналу і його копії:

(7.7) Фізичний зміст – це середня взаємна потужність сигналуі його копії. Наприклад, для сигналу, АКФ має вигляд

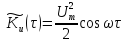(7.8)

Ця АКФ сама є періодичною косинусоїдою, при її значенняявляє собою середню(ефективну) потужність, що виділяється сигналом на активному навантаженні 1 Ом.

3. Існує тісний зв'язок між автокореляційною функцією і енергетичним спектром сигналу.

За формулою (7.1), АКФ – це скалярний добуток . У той самий час, за узагальненою формулою Релея цей скалярний добуток

Оскільки спектральна щільність зміщеного у часі сигналу

,

то комплексно-спряжена його щільність

.

І тоді АКФ сигналу набуває виразу

(7.9)

У формулі (7.9) квадрат модуля спектральної щільності – це енергетичний спектр сигналу. З (7.9) випливає, що енергетичний спектр і АКФ сигналу зв’язані перетворенням Фур’є:, і тоді парне співвідношення до (7.9):

(7.10)

Вирази (7.9) і (7.10) є засадничо важливими з двох причин:

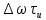
1. Вони дають можливість оцінювати кореляційні властивості сигналів, виходячи з розподілу їх енергії по спектру. Принцип неозначеності (див. лекцію 1) вказує на те, що чим уширшій смузі частот розподілені спектральні компоненти сигналу, тим вужчою є основний пелюсток АКФ і тим досконалішим є сигнал з точки зору можливості точного вимірювання моменту його виникнення.

2. Формули (7.9) і (7.10) вказують на спосіб експериментального визначення енергетичного спектра: часто зручніше спочатку одержати АКФ, а потім, застосовуючи пряме перетворення Фур’є (7.10), знайти енергетичний спектр сигналу.

4. Взаємна кореляційна функція (ВКФ) в уніфікований спосіб описує як різницю у формі сигналів, так і їхнє взаємне положення на осі часу.

За аналогією з (7.1) для АКФ, ВКФ визначається для двох дійсних сигналів і:

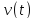(7.11)

Мету застосування ВКФ можна пояснити на прикладі. Нехай сигнал і у початковому стані ортогональні, тобто

.

При проходженні цих сигналів через певний пристрій сигнал буде зсунутий відносно сигналуна деякий проміжок часу. Тоді ВКФслугуємірою стійкості ортогонального стану відносно зсуву сигналів у часі.

Властивості ВКФ.

1. . Одне і те саме положення сигналів і досягається як при запізненні відносно, так і його випередженні на один і той самий час.

. ВКФ не є парною функцією аргумента :

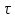3. . ВКФ обмежена, і це випливає із нерівності Коші-Буняковського: зсув сигналу у часі не впливає на величину його норми.

4. ПриВКФ зовсім необов’язково досягає максимуму.

Приклад. Маємо сигнали – прямокутний відеоімпульс,– трикутний відеоімпульс (рис. 7.4)

Рисунок 7.4

У межах

;.

Уведемо відносний час .

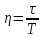Тоді при

,

при

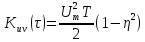
Побудова ВКФ засвідчує, що вона несиметрична (рис. 7.5)

Рисунок 7.5

Виразимо ВКФ через спектральні характеристики сигналів і . На підставі узагальненої формули Релея

.

Оскільки спектр зміщеного у часі сигналу

,

то

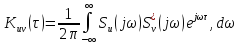(7.12)

У формулі (7.12)

–(7.13)

це взаємна спектральна щільність сигналів і .

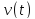Відтак, ВКФ і взаємний енергетичний спектр двох сигналів зв’язані парою перетворень Фур’є:

(7.14)