Лекція 2(16). Спектри неперіодичних сигналів

1. Спектральне подання неперіодичних сигналів.

2. Спектр прямокутного відеоімпульса.

3. Спектри деяких неперіодичних сигналів.

4. Спектри серії імпульсів.

1. Дуже важливим на практиці є неперіодичні сигнали – напр., поодинокі імпульси, серії імпульсів. Вони не можуть бути подані у вигляді ряду Фур’є. Аби застосувати до них спектральний метод опису, треба вважати ці сигнали періодичними функціями з періодом .

Скористаємося найзручнішою комплексною формою запису ряду Фур’є (див. л. 1):

, (2.1)

де коефіцієнти (комплексні амплітуди) розраховуються як

(2.2)

Підставимо (2.2) в (2.1), позначивши інтервал між частотами сусідніх гармонік , одержимо

(2.3)

При збільшенні періоду 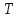амплітуда гармонік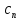зменшується, інтервалзменшується і лінійчастий спектр дедалі “згущується”. У граничному переході при, , і спектр із дискретного стає суцільним. При цьому сума в правій частині (2.3) переходить в інтеграл

(2.4)

Останній вираз являє собою суму нескінченно великого числа гармонічних функцій із нескінченно малими амплітудами і частотами , які проходять увесь спектр віддо. Відтак неперіодичні сигнали характеризуються неперервним, суцільним спектром частот, тоді як періодичні – дискретним, або лінійчастим спектром.

Формулу (2.4) можна подати у такому вигляді:

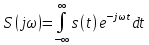; (2.5)

(2.6)

Формула (2.5) – пряме перетворення Фур’є; (2.6) – зворотне перетворення Фур’є, і вони часто позначаються як

(2.7)

(2.8)

Пряме перетворення Фур’є дозволяє перейти з часової області подання функції на комплексну частотну площину, а зворотне перетворення, навпаки, – з комплексної частотної площини на часову.

Основні властивості перетворення Фур’є

1.Лінійність .

2.Теорема інтегрування .

3.Теорема диференціювання .

4.Теорема подібності (масштабу) Аби стиснути сигнал у часі, зберігаючи форму, слід розширити його спектр при пропорційному зменшенні амплітуд гармонік.

5.Теорема про зсув (запізнення)

.

6. Теорема про згортку.

,

де згортка спектрів;

–згортка сигналів.

7. Теорема Релея

,

де – спектральна щільність сигналу.

Проводячи аналогію між рядом Фур’є і інтегралом Фур’є:

і ,

можна прийти до відношення

, (2.9)

де .

Через те спектральна щільність має фізичний зміст щільності амплітуд і володіє розмірністю амплітуди, поділеної на герц.характеризує гармоніку частотиза амплітудою і фазою. Із (2.9) випливає, що огинаюча суцільного спектранеперіодичної функції і огинаюча лінійчастого спектра періодичної функціїзбігаються за формою і відрізняються лише масштабом:

Пряме перетворення Фур’є і зворотне перетворення Фур’є мають симетричну природу, і це зумовлено дуальністю частоти і часу.

(2.10)

(2.11)

Інакше кажучи, якщо спектром функції є, то спектром функції є функція

2. Нехай маємо сигнал – поодинокий прямокутний відеоімпульс (рис 2.1)

Рисунок 2.1

(2.12)

Спектральна щільність сигналу (2.12):

(2.13)

де – № арки

АЧС сигналу

(2.14)

ФЧС сигналу

) (2.15)

Рисунок 2.2

АЧС сигналу (рис. 2.2 а) істотно залежить від тривалості імпульсу , але не зв’язаний з 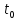. ФЧС (рис. 2.2 б), навпаки, визначається часом запізнення .

3. Радіоімпульс. Нехай маємо поодинокий прямокутний радіоімпульс (рис. 2.3)

Рисунок 2.3

(2.16)

Спектральна щільність сигналу (2.16)

(2.17)

Розпишемо функцію (2.17) окремо для АЧС І ФЧС і для додатніх і для від’ємних частот:

для (2.18)

для (2.19)

АЧС і ФЧС, побудовані за виразами (2.18) і (2.19), наведені на рис. 2.4.

Рисунок 2.4

Спектри прямокутного радіоімпульсу практично відрізняється від спектрів прямокутного відеоімпульсу лише зміщенням по осі частот на величину і зменшенням удвічі модуля спектральної щільності.

Гаусовий імпульс. Цей сигнал (рис 2.5) називається ще дзвоноподібним.

Рисунок 2.5

, (2.20)

де – стала, що визнає тривалість імпульсу.

Спектральна щільність

(2.21)

Внаслідок парності функції (2.20) спектр її є дійсним і також має дзвоноподібну, гаусову форму (рис. 2.6).

Рисунок 2.6

Для гаусового імпульсу, як уже згадувалося, , а саме .Найменша ширина спектра зумовлює найбільшу завадостійкість сигналу.

Експоненційний імпульс.

Часова діаграма сигналу (рис. 2.7) побудована за аналітичним його виразом:

(2.22)

Рисунок 2.7

Спектральна щільність

(2.23)

АЧС (рис. 2.8а)

ФЧС (рис. 2.8б)

Рисунок 2.8

Трикутний відеіомпульс

Рисунок 2.9

Рисунок 2.10

Експоненційний радіоімпульс

Рисунок 2.11

Рисунок 2.12

Дельта-функція. Спектральна щільність дельта-функції (рис. 2.13)

(2.24)

Рисунок 2.13

Рисунок 2.14

Із частотно-часової дуальності перетворення Фур’є випливає: якщо спектром дельта функції є 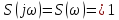то спектром функціїбуде фунція(рис. 2.14) із нескінченно малою шириною спектра. З цього випливає, що і спектральні функції гармонічного сигналуявляють собою-функції (рис. 2.15).

Рисунок 2.15

Функція Хевісайда

Спектральна щільність функції вмикання

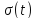
(2.25)

Графічний образ цієї функції показаний на рис. 2.16.

Рисунок – 2.16

У формулі (2.25) перший член правої частини – це спектральна щільність миттєвого перепаду функції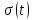в момент(бічні смуги спектру). Другий член– спектральна щільність постійної складової функції вмикання.

4. Нехай маємо сигнал у вигляді серії з імпульсів (рис. 2.17). Згідно з теоремою лінійності і теореми про зсув для перетворення Фур’є спектральна щільність сигналу

(2.26)

Рисунок 2.17

Модуль спектральної щільності серії імпульсів

(2.27)

Пронормуємо вираз (2.27) через його значення при

, (2.28),

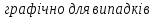
де – модуль нормованої АЧС імпульсу в серії,– функція частоти що не залежить від форми імпульсів і визначається їх числомв серії з періодом їх слідування. Побудуємо функціюі (рис.2.18).

Рисунок 2.18

Як свідчать ці графіки, в інтервалі частот від 0 до чисельник дробу, а відтак функціяприймає нульове значенняразів. Періодичність чисельника функціївразів вища, ніж знаменника. Графіки функціїпелюсткової структури (рис. 2.18); мають великі і малі пелюстки. Висота великих пелюстків . Висота малих пелюстків визначається локальними максимумами функції. Значеннярозраховуються у ході розрахунку функції; вони також табульовані [1]. Так при ; при при; при ; при . 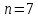Великі пелюстки вдвічі ширші від малих.

Рисунок 2.19

Вираз (2.28) справедливий для серії імпульсів довільної форми. За його допомогою, знаючи АЧС імпульса в серії і вид функції , можна побудувати спектр усієї серії імпульсів простим перемноженням ординат графіків функційі.

Спектри серії імпульсів для різних показані на рис 2.19.

Зі збільшенням (числа імпульсів в серії) великі пелюстки звужуються, висота малих пелюстків зменшується, а їх число зростає; спектр поступово вироджується із суцільного в лінійчастий і приперетворюється у дискретний.