
- •V. Спектральний аналіз детермінованих сигналів. Модуляція Лекція 1(15). Спектри періодичних сигналів
- •Лекція 2(16). Спектри неперіодичних сигналів
- •Лекція 3(17). Енергетичний спектр. Модуляція
- •Лекція 4 (18). Кутова модуляція сигналів
- •VI. Спектральний аналіз проходження детермінованих сигналів через лінійні кола Лекція 5 (19). Спектральний метод розрахунку реакції лінійного кола на детерміновані сигнали
- •Лекція 6 (20). Зв'язок частотних і часових характеристик лінійних кіл і детермінованих сигналів
- •VII Кореляційний аналіз детермінованих сигналів Лекція 7 (21). Автокореляція і взаємна кореляція сигналів
- •VIII Випадкові сигнали і перетворення їх характеристик в лінійних колах Лекція 8 (22). Випадкові величини
- •Лекція 9 (23). Стаціонарні випадкові величини в часовому і спектральному вимірі
- •Лекція 10 (24). Вузькосмугові детерміновані і випадкові сигнали
- •Лекція 11 (25). Перетворення характеристик випадкового процесу у лінійному колі
- •Список літератури
V. Спектральний аналіз детермінованих сигналів. Модуляція Лекція 1(15). Спектри періодичних сигналів
Поняття сигналу.
Спектральний спосіб опису періодичних сигналів. Ряд Фур’є.
Спектри періодичної послідовності відеоімпульсів.
Спектр періодичної послідовності радіоімпульсів.
Зв’язок між формою сигналу та його спектром.
1. Сигналом (від лат. signum – знак) називається процес зміни у часі фізичного стану якогось об’єкта, призначений для передачі, відображення, реєстрації повідомлень (інформації). Будь який сигнал можна спостерігати емпірично (за допомогою осцилографа, приймача, засобів відображення інформації, вимірювального приладу тощо). Але емпіричне спостереження дозволяє аналізувати лише часткові, одиничні явища сигналів і унеможливлює розкриття фундаментальних властивостей – напр., для передбачення їх поведінки в нових, змінених умовах. Тому застосовують описи через їх математичні моделі.
Математична
модель – це функція часу. Наприклад,
неперервний сигнал (гармонічне коливання)
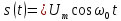 ,
,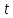 є
є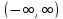 ;
неперервний сигнал (гаусовий імпульс)
;
неперервний сигнал (гаусовий імпульс)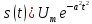 ,
, є
є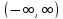 ;
фінітний сигнал (той, що існує на
обмеженому часовому інтервалі) –
трикутний відеоімпульс
;
фінітний сигнал (той, що існує на
обмеженому часовому інтервалі) –
трикутний відеоімпульс
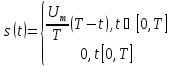 ;
;
періодичний
сигнал
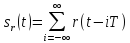 ,
,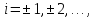 де
де
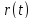 – фінітний на інтервалі
– фінітний на інтервалі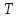 (періоді послідовності) сигнал і т.п.
Модель сигналу дозволяє абстрагуватися
від конкретної природи його носія: одна
і та сама модель може адекватно описувати
струм, напругу, напруженість поля,
потужність тощо. До того ж модель описує
засадничі
головні
властивості сигналів, оминаючи їх
другорядні властивості.
(періоді послідовності) сигнал і т.п.
Модель сигналу дозволяє абстрагуватися
від конкретної природи його носія: одна
і та сама модель може адекватно описувати
струм, напругу, напруженість поля,
потужність тощо. До того ж модель описує
засадничі
головні
властивості сигналів, оминаючи їх
другорядні властивості.
Класичні способи опису сигналів – це часовий і спектральний. У першому способі сигнал подається як функція часу (математична модель). Другий спосіб полягає в описі сигналу через суму ортогональних складових, що утворюють ортонормовану систему гармонік, тобто у розкладенні сигналу в ряд Фур’є.
2.
Будь-яка
періодична функція
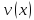 з періодом
з періодом ,
яка задовольняє у межах періоду умовам
Диріхле, може бути представлена через
ряд Фур’є, який ще називається
тригонометричним, або гармонічним:
,
яка задовольняє у межах періоду умовам
Диріхле, може бути представлена через
ряд Фур’є, який ще називається
тригонометричним, або гармонічним:
 ,
(1.1)
,
(1.1)
де
 (1.2)
(1.2)
Нехай
періодичний сигнал описується функцією
часу
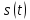 з довільним періодом
з довільним періодом . Увівши
нову змінну
. Увівши
нову змінну
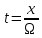 ,
перейдемо до функції
,
перейдемо до функції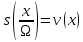 з
періодом
з
періодом
 ,
яку можна розкласти в ряду Фур’є за
формулами (1.1) і (1.2). Для функції
,
яку можна розкласти в ряду Фур’є за
формулами (1.1) і (1.2). Для функції
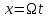 ;
;

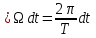 ;
;
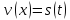 .
Тоді
функція
.
Тоді
функція
 набуде вигляду
набуде вигляду
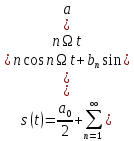 ,
(1.3)
,
(1.3)
де
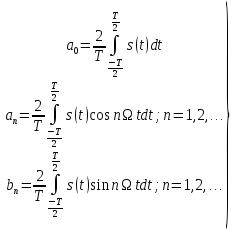 (1.4)
(1.4)
або в іншій формі
 (1.5)
(1.5)
де
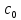 =
= ;
;
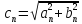 ;
;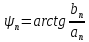 (1.6)
(1.6)
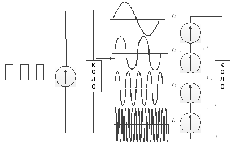
Рисунок 1.1
Відтак,
періодичний сигнал можна представити
у вигляді накладення постійної складової
і нескінченного числа синусоїдних
(гармонічних) коливань з частотами
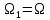 ;
; ;
;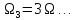 , амплітудами
, амплітудами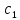 ,
, ,
,
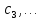 і початковими фазами
і початковими фазами
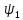 ,
,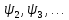 (рис. 1.1).
(рис. 1.1).
Гармонічні
коливання з частотами
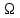 ,
,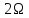 ,
,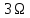 називаються першою (основною), другою,
третьою і т.д. гармоніками відповідно.
Постійна складова дорівнює середньому
значенню коливання за період.
називаються першою (основною), другою,
третьою і т.д. гармоніками відповідно.
Постійна складова дорівнює середньому
значенню коливання за період.
Повний
спектральний опис сигналу охоплює:
послідовність величин
 спектр частот;
спектр частот;
 –
спектр
амплітуд;
–
спектр
амплітуд;
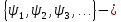 спектр фаз.
спектр фаз.
 Рисунок
1.2
Рисунок
1.2
Більше
практичне застосування одержали
амплітудно-частотний
спектр
(АЧС) – сукупність спектральних ліній,
перпендикулярних до осі частот, які
відкладені у точках
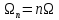 (
(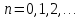 ),
так що ординати їх дорівнюють значенням
),
так що ординати їх дорівнюють значенням
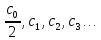 ,
іфазо-частотний
спектр
(ФЧС) з ординатами
,
іфазо-частотний
спектр
(ФЧС) з ординатами
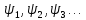 ,
(рис 1.2)
,
(рис 1.2)
При комплексній формі запису ряда Фур’є
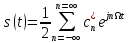 (1.7)
(1.7)
комплексні амплітуди гармонік визначаються
 (1.8)
(1.8)
У випадку комплексної форми ряду Фур’є шкала частот отримує додатково від’ємну напіввісь і АЧС стає симетричним відносно осі ординат, а ФЧС – відносно початку відліку координат (рис 1.3)
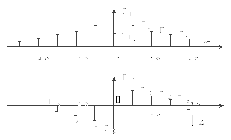
Рисунок 1.3
Часовий і спектральний способи опису сигналів рівноправні і взаємозамінні; це різні форми подання реально існуючих процесів. Позаяк час і частота є дуальними величинами, то дуальними є і відповідні форми описів сигналів.
3. Нехай маємо сигнал у вигляді періодичної послідовності відеоімпульсів прямокутної форми, часова діаграма якої приведена на рис. 1.4.
 Рисунок
1.4
Рисунок
1.4
На
цьому рисунку
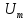 – амплітуда
сигналу,
– амплітуда
сигналу,
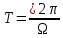 –
період слідування,
–
період слідування,
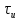 –
тривалість імпульсу. Функція
–
тривалість імпульсу. Функція
 у межах періоду може бути описана виразом
у межах періоду може бути описана виразом
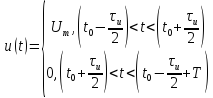 (1.9)
(1.9)
Визначимо ряд Фур’є, що описує даний сигнал. Комплексні коефіцієнти, або амплітуди гармонік цього ряду визначаються за (1.8).

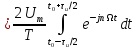
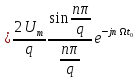 ,
(1.10)
,
(1.10)
де
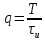 – шпаруватість імпульсів.
– шпаруватість імпульсів.
Із
(1.10) випливає, що
 – модуль комплексного коефіцієнта,
– модуль комплексного коефіцієнта, – аргумент його, і тоді відповідно до
ряду Фур’є (1.7) одержуємо
– аргумент його, і тоді відповідно до
ряду Фур’є (1.7) одержуємо
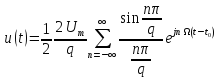 (1.11)
(1.11)
розклад сигналу (1.9) в ряд Фур’є. Дійсна форма цього ряду
 (1.12)
(1.12)
відповідає
виразу (1.5). В (1.12) перший член
 – постійна складова,
– постійна складова,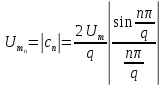 –амплітуда
–амплітуда
 -ої
гармоніки сигналу
-ої
гармоніки сигналу
 .
Проаналізуємо
одержані формули ряду
Фур’є
сигналу
.
Проаналізуємо
одержані формули ряду
Фур’є
сигналу
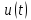 (1.11) і (1.12).
(1.11) і (1.12).
1.
Постійна складова
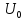 і амплітуди
і амплітуди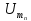 гармонік пропорційні до амплітуди
імпульсів
гармонік пропорційні до амплітуди
імпульсів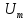 і зменшуються зі зростанням їх шпаруватості
і зменшуються зі зростанням їх шпаруватості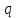 ,
що викликано зменшенням середньої за
період енергії імпульсу.
,
що викликано зменшенням середньої за
період енергії імпульсу.
2.
Амплітуди
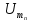 не залежать від задержки імпульсу у
часі
не залежать від задержки імпульсу у
часі ,
а залежать від шпаруватості. Натомість
початкові фази
,
а залежать від шпаруватості. Натомість
початкові фази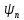 гармонік залежать лише від зсуву
імпульсів
гармонік залежать лише від зсуву
імпульсів ,
а не від амплітуди і тривалості імпульсів.
Відтак зсув сигналу у часі
,
а не від амплітуди і тривалості імпульсів.
Відтак зсув сигналу у часі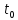 визначає його ФЧС і не впливає на його
АЧС.
визначає його ФЧС і не впливає на його
АЧС.
3.
Розподіл амплітуд гармонік підлягає
закону аркового синуса
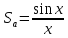 .
Така
функція має аркову структуру (рис. 1.5) і
визначає появу перед амплітудами знаку
«+»
або
«
.
Така
функція має аркову структуру (рис. 1.5) і
визначає появу перед амплітудами знаку
«+»
або
«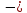 »,
що відповідає зміні від арки до арки
фази гармонік на
»,
що відповідає зміні від арки до арки
фази гармонік на .Через
це вираз (1.12) можна записати інакше:
.Через
це вираз (1.12) можна записати інакше:

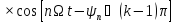 (1.13)
(1.13)
де
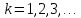 –
номер арки (інтервал значень змінної
–
номер арки (інтервал значень змінної
 , за яких функція
, за яких функція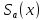 приймає
певні за знаком («+»
або
«
приймає
певні за знаком («+»
або
« »)
значення).
»)
значення).
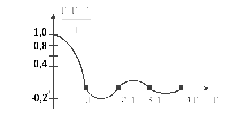
Рисунок 1.5
4.
Спектральні лінії АЧС і ФЧС віддалені
від сусідніх на величину частоти
слідування імпульсів
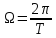 . Розподіл спектральних ліній за висотою
визначаєтьсяогинаючою
спектру,
характер якої залежить від форми сигналу.
. Розподіл спектральних ліній за висотою
визначаєтьсяогинаючою
спектру,
характер якої залежить від форми сигналу.
АЧС. Огинаюча АЧС періодичної послідовності відеоімпульсів

перетинає
вісь частот, коли аргумент кратний
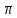 ,
тобто
,
тобто
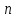 кратний
кратний
 – на частотах, кратних шпаруватості.
Тому гармоніки з частотами
– на частотах, кратних шпаруватості.
Тому гармоніки з частотами .
На
рис. 1.6 показаний нормований АЧС
.
На
рис. 1.6 показаний нормований АЧС
 сигналу
сигналу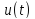 (1.9) при
(1.9) при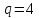 .
Під першими арками зосереджена основна
частина енергії
сигналу,
і
тому
ефективна
ширина
спектра
.
Під першими арками зосереджена основна
частина енергії
сигналу,
і
тому
ефективна
ширина
спектра


Рисунок 1.6
На
рис. 1.7 досліджується, як впливає на АЧС
зміна
 і частоти слідування
і частоти слідування .
Зі зменшенням частоти слідування
.
Зі зменшенням частоти слідування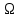

 відбувається “згущення” спектра:
відстані між лініями зменшуються. Ширина
спектра не змінюється, а основна частина
енергії розподіляється на більшому
числі гармонік. При збільшенні
відбувається “згущення” спектра:
відстані між лініями зменшуються. Ширина
спектра не змінюється, а основна частина
енергії розподіляється на більшому
числі гармонік. При збільшенні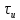 при
при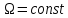 ширина арок і ширина спектра зменшується
(відносне стиснення спектра). Основна
частина енергії розподіляється на
меншому числі гармонік і зосереджується
в області щоразу нижчих частот. Відтак,
що коротше імпульси і більша їх
шпаруватість, то ширший і густіший їхній
спектр, і навпаки.
ширина арок і ширина спектра зменшується
(відносне стиснення спектра). Основна
частина енергії розподіляється на
меншому числі гармонік і зосереджується
в області щоразу нижчих частот. Відтак,
що коротше імпульси і більша їх
шпаруватість, то ширший і густіший їхній
спектр, і навпаки.
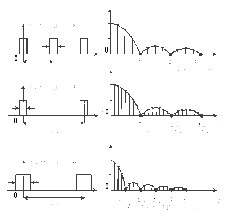
Рисунок 1.7
ФЧС. Із виразів (1.12) і (1.13) випливає, що початкові фази гармонік визначаються
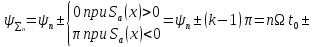
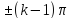 (1.14)
(1.14)

Рисунок 1.8
Відтак
огинаючою ФЧС є пряма з кутом нахилу
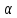 ,
який залежить від зсуву імпульсів
,
який залежить від зсуву імпульсів .
Урахування зміни фази гармонік на
.
Урахування зміни фази гармонік на від арки до арки здійснюється відповідним
зміщенням цієї прямої паралельно на
від арки до арки здійснюється відповідним
зміщенням цієї прямої паралельно на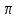 вгору або вниз. Кожна арка,
як відомо, має ширину
вгору або вниз. Кожна арка,
як відомо, має ширину
 .
Тому величина зсуву фази на арку складає
кут
.
Тому величина зсуву фази на арку складає
кут
 ,
(1.15)
,
(1.15)
де
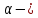 кут нахилу огинаючої ФЧС,
кут нахилу огинаючої ФЧС,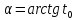 .
.
Що
більше зсув імпульсів у часі, то більше
нахил огинаючої їх ФЧС. При
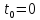 кут
кут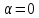 (рис. 1.8).
(рис. 1.8).
4.
Нехай маємо сигнал
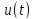 (рис.1.9)
– періодичну послідовність прямокутних
радіоімпульсів. Його аналітичний вираз
(рис.1.9)
– періодичну послідовність прямокутних
радіоімпульсів. Його аналітичний вираз
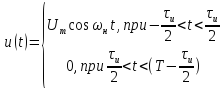 (1.16)
(1.16)

Рисунок 1.9
На
рисунку
 – частота слідування імпульсів,
– частота слідування імпульсів,
 – несуча частота.
– несуча частота.
Застосувавши
до сигналу
 процедуру визначення ряду Фур’є з
попереднього питання, одержимо згідно
до форми цього ряду (1.5):
процедуру визначення ряду Фур’є з
попереднього питання, одержимо згідно
до форми цього ряду (1.5):
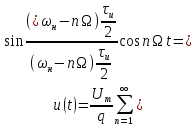
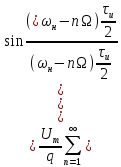 (1.17)
(1.17)
Із
(1.17) випливає, що огинаюча АЧС послідовності
прямокутних радіоімпульсів визначається
функцією
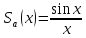 ,
які для послідовності відеоімпульсів.
Різниця лише в тому, що ця функція зміщена
по осі частот на величину
,
які для послідовності відеоімпульсів.
Різниця лише в тому, що ця функція зміщена
по осі частот на величину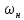 і її максимум при
і її максимум при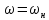 вдвічі менший, ніж у випадку відеоімпульсів
(рис. 1.10).
вдвічі менший, ніж у випадку відеоімпульсів
(рис. 1.10).
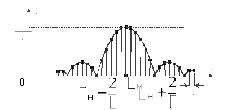
Рисунок 1.10
Відтак
спектр послідовності прямокутних
радіоімпульсів збігається зі спектром
послідовності прямокутних відеоімпульсів,
зміщених управо по осі частот на величину
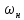 .
Ефективна ширина спектра радіоімпульсів
вдвічі більша, ніж у однакових за
тривалістю відеоімпульсів.
.
Ефективна ширина спектра радіоімпульсів
вдвічі більша, ніж у однакових за
тривалістю відеоімпульсів.
5. Форма сигналу вповні визначається лише сукупністю АЧС і ФЧС: маючи АЧС, можна судити про форму сигналу, і навпаки.

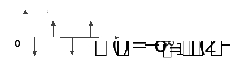
Рисунок 1.11
Нехай
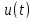 – функція часу, сигнал. Нехай
– функція часу, сигнал. Нехай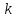 -та
похідна
-та
похідна
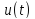 містить дельта-функції (на рис 1.11 –
третя похідна). Тоді для коефіцієнтів
ряду Фур’є розкладу функції
містить дельта-функції (на рис 1.11 –
третя похідна). Тоді для коефіцієнтів
ряду Фур’є розкладу функції справедливі нерівності
справедливі нерівності
 ;
;
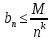 ,
(1.18)
,
(1.18)
де
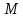 – стала,
що
залежить
від
форми
сигналу.
Із рис. 1.11 видно, що ряд Фур’є трикутних
імпульсів сходиться швидше (амплітуди
гармонік спадають швидше при зростанні
їх номеру), ніж у випадку прямокутних
імпульсів. Відтак, швидкість спаду
амплітуд гармонік у спектрі залежить
від структури сигналу: коефіцієнти
спадають тим швидше, чим “гладшою” є
форма сигналу. Якщо сигнал має
стрибкоподібні переходи (його функція
має скінченні розриви) і в його першій
похідній з’являються дельта-імпульси,
то амплітуда гармонік спадає повільно,
за законом
– стала,
що
залежить
від
форми
сигналу.
Із рис. 1.11 видно, що ряд Фур’є трикутних
імпульсів сходиться швидше (амплітуди
гармонік спадають швидше при зростанні
їх номеру), ніж у випадку прямокутних
імпульсів. Відтак, швидкість спаду
амплітуд гармонік у спектрі залежить
від структури сигналу: коефіцієнти
спадають тим швидше, чим “гладшою” є
форма сигналу. Якщо сигнал має
стрибкоподібні переходи (його функція
має скінченні розриви) і в його першій
похідній з’являються дельта-імпульси,
то амплітуда гармонік спадає повільно,
за законом
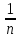 .
Якщо ж сигнал неперервний, але в його
першій похідній є скінченні розриви, а
в другій дельта-імпульси, то амплітуда
гармонік спадає швидше, пропорційно до
.
Якщо ж сигнал неперервний, але в його
першій похідній є скінченні розриви, а
в другій дельта-імпульси, то амплітуда
гармонік спадає швидше, пропорційно до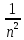 і т.д. Отже, що швидше спадають коефіцієнти
Фур’є, то “гладша” форма сигналу, то
менша ширина його спектра. “Найгладшим”
є моногармонічне коливання (рис. 1.11).
і т.д. Отже, що швидше спадають коефіцієнти
Фур’є, то “гладша” форма сигналу, то
менша ширина його спектра. “Найгладшим”
є моногармонічне коливання (рис. 1.11).
Для імпульсних сигналів справедлива рівність.
 ,
(1.19)
,
(1.19)
де
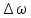 – ширина спектра сигналу,
– ширина спектра сигналу, – тривалість сигналу. Тривалість сигналу
і його протяжність у частоті зв’язаніспіввідношенням
неозначеності:
що ширший спектр, то менша тривалість,
і навпаки.
– тривалість сигналу. Тривалість сигналу
і його протяжність у частоті зв’язаніспіввідношенням
неозначеності:
що ширший спектр, то менша тривалість,
і навпаки.
“Найгладші” сигнали, з найбільш плавною зміною у часі мають
 .
.
Такими сигналами є дзвоноподібні (гаусові) імпульси (див. перше питання даної лекції). Саме в них необхідність зменшення тривалості не призводить до великого розширення спектра.
