Физика / 3 РАБОТА И ЭНЕРГИЯ

РАБОТА И ЭНЕРГИЯ. ЗАКОНЫ СОХРАНЕНИЯ.

Энергия, работа, мощность

Энергия – мера различных форм движения и взаимодействия. Изменение механического движения тела вызывается внешними силами. При таком взаимодействии идет обмен энергией. Для описания этого процесса вводится понятие работы силы. Если тело движется прямолинейно и на него действует постоянная сила , то

Рис.

В общем случае сила изменяется по модулю и направлению, поэтому следует пользоваться элементарной работой. Это позволяет избежать ошибок.

Рис.

Для бесконечно малого перемещения имеем . Это означает, что длина пути равна перемещению . Полная работа равна

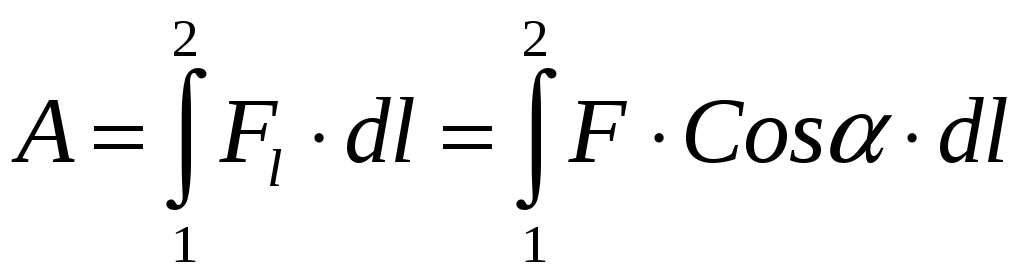
Работа, в общем случае, зависит от пути. Единица измерения работы – джоуль (Дж). 1 Дж=1Н∙м.

Работа в единицу времени – мощность.

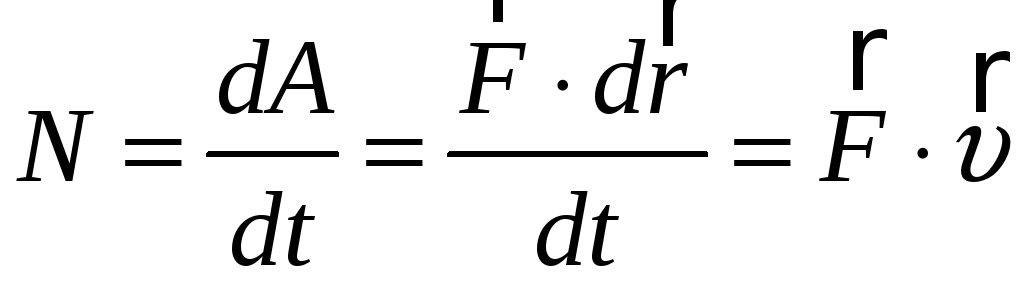
Единица измерения мощности – ватт. 1вт=1Дж/с.

Сила, действующая на тело, изменяет его скорость. Она совершает работу. Эта работа идет на изменение кинетической энергии . . Найдем выражение для кинетической энергии.

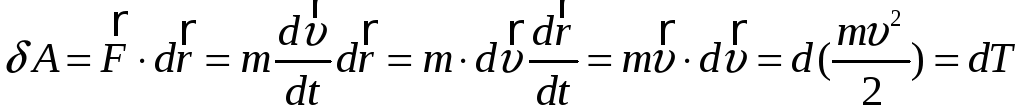
Отсюда 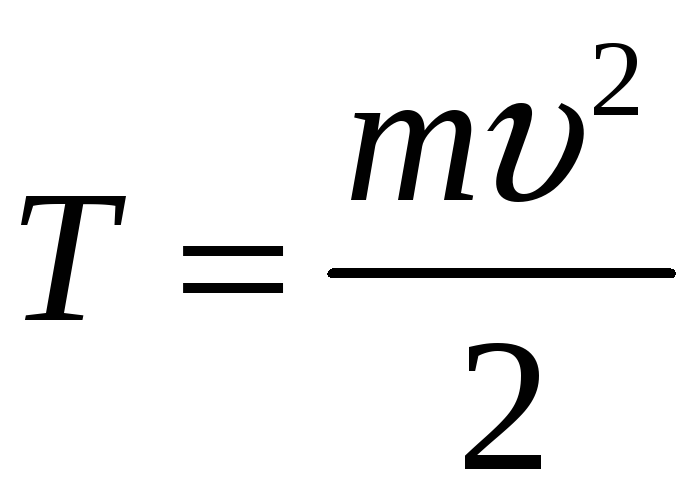- кинетическая энергия. Кинетическая энергия системы равна сумме кинетических энергий всех тел, входящих в систему.

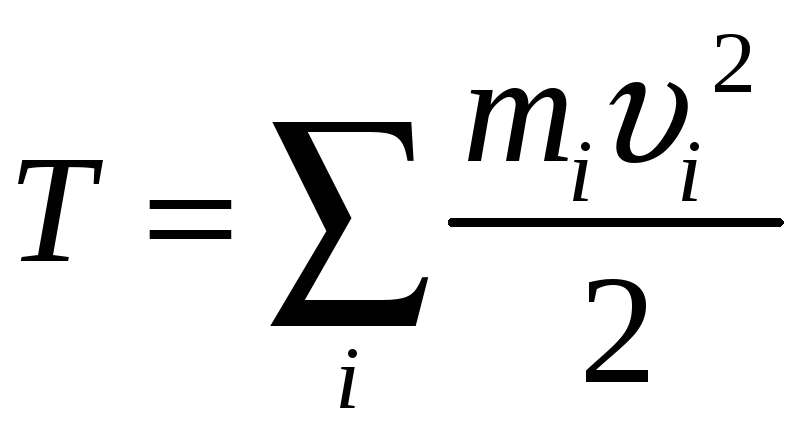
Если работа по перемещению системы не зависит от пути, а определяется только начальной и конечной токами, то такие силовые поля называются потенциальными, а силы консервативными. Взаимодействие между телами осуществляется за счет силовых полей. Вводится понятие потенциального поля сил. Тела в таких полях обладают потенциальной энергией, . Она определяется взаимным расположением тел и характером сил взаимодействия между телами. Работа консервативных сил при элементарном изменении конфигурации расположения тел равна изменению потенциальной энергии. . - потенциальная энергия.

Так как , то . Для конечного изменения расположения тел , где - постоянная. Для консервативных сил 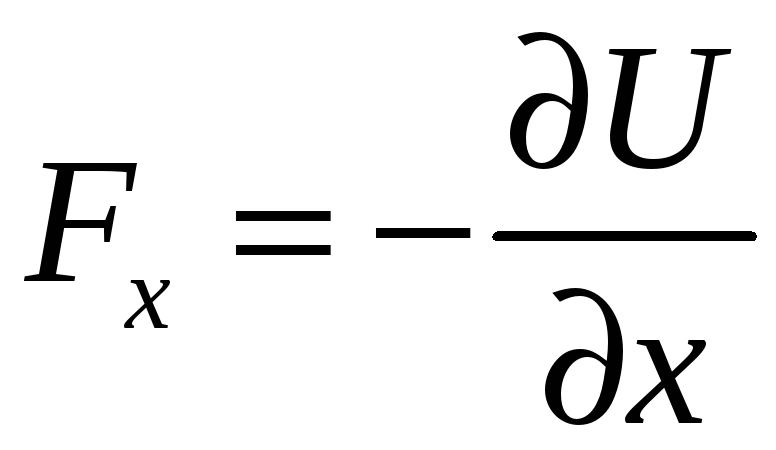, , 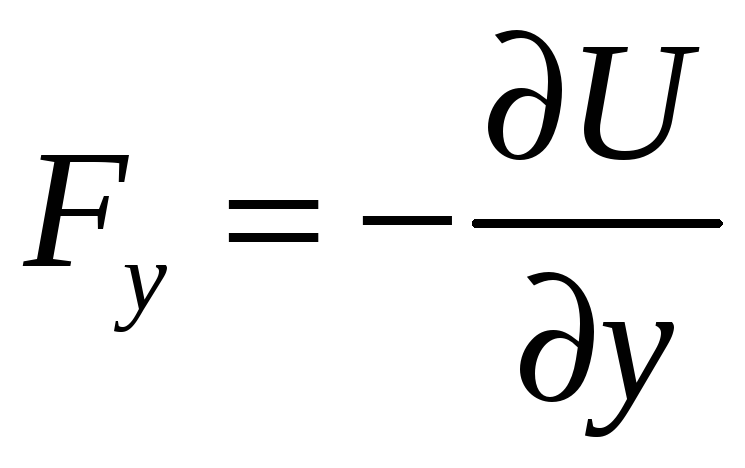. Это можно записать в виде .

Сила есть градиент потенциальной энергии. Для потенциальных полей работа определяется начальной и конечной точкой. В этом случае элементарное изменение работы можно заменить полным дифференциалом работы. . Значение потенциальной энергии зависит от выбора начала отсчета. Однако это не влияет на уравнения движения. Потенциальная энергия в поле тяготения .

Сила упругости

Рассмотрим пружину. Сила упругости пропорциональна деформации пружины (Гук)

- коэффициент жесткости, - деформация пружины. Это соотношение справедливо для твердых тел. В векторном виде

Элементарная работа силы упругости – это произведение величины силы на элементарную деформацию.

Работа, совершаемая пружиной положительная, над пружиной отрицательная. Полная работа

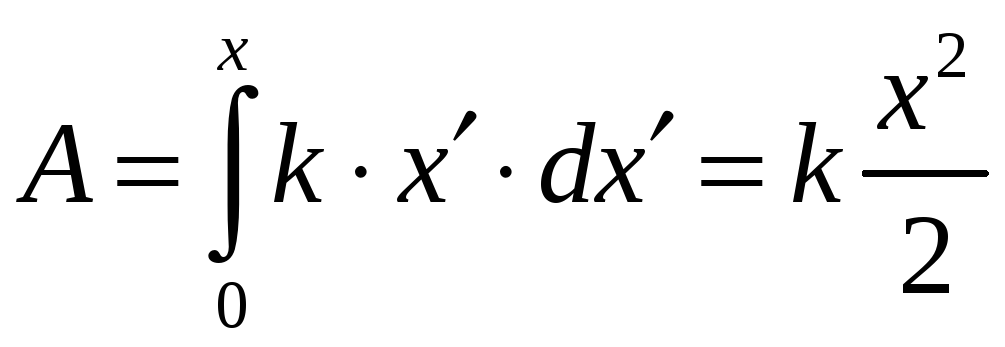
Эта работа идет на увеличение потенциальной энергии пружины

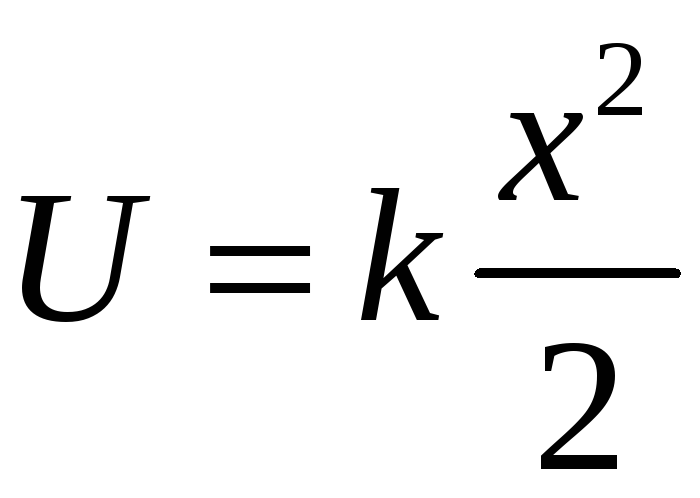
Полная энергия системы .

Закон сохранения энергии

Идея принадлежит М.В. Ломоносову. Количественная формулировка – Майер, Гельмгольц. Пусть система состоит из материальных точек, взаимодействие которых происходит за счет консервативных внутренних сил . На систему действуют консервативные внешние силы . Кроме этих сил на систему действуют неконсервативные силы . Тогда, согласно второму закону Ньютона на каждую материальную точку действуют силы

(1)

За время все точки перемещаются на расстояние . Умножим Ур.(1) на и просуммируем по всем точкам.

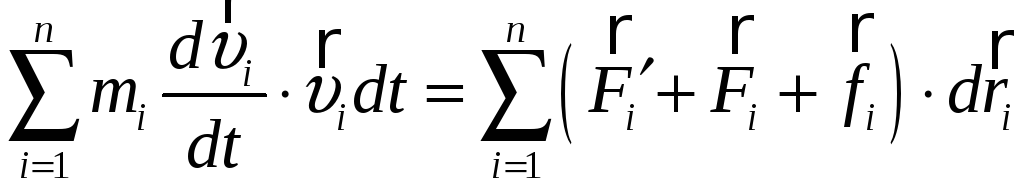
После группировки, получим

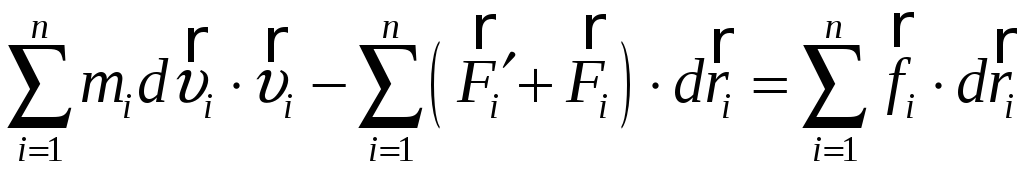(2)

Введем

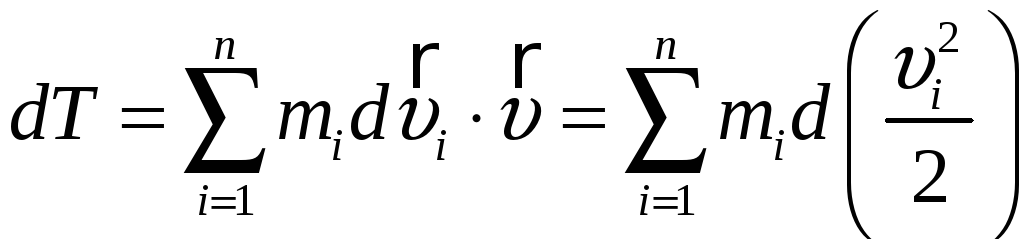- изменение кинетической энергии частиц. Слагаемое 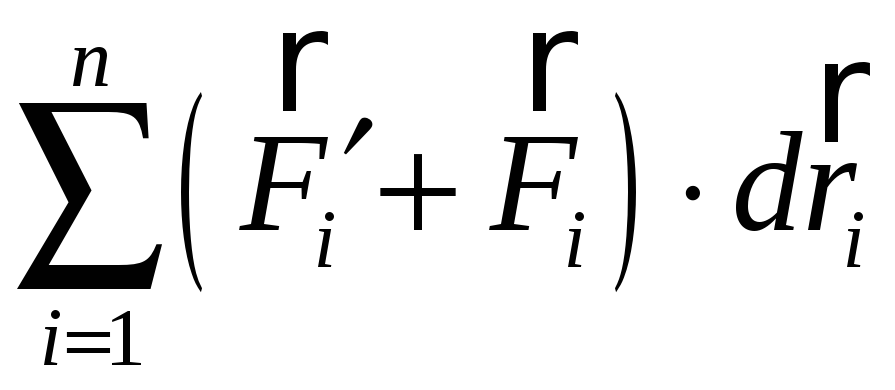- элементарная работа внутренних и внешних консервативных сил. Она равна элементарному изменению потенциальной энергии со знаком минус.

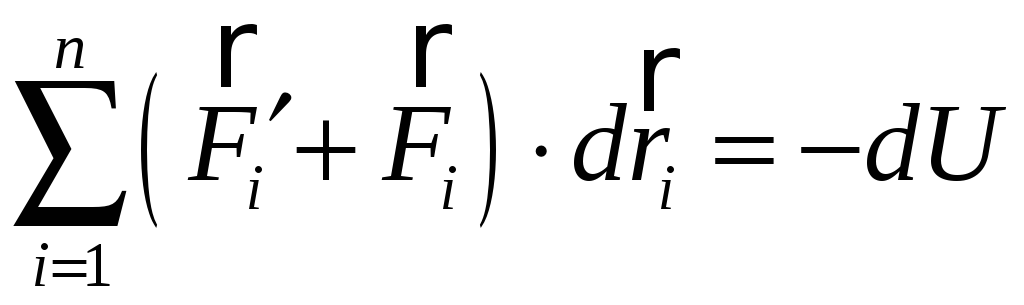
Правая часть Ур.(2) работа неконсервативных сил

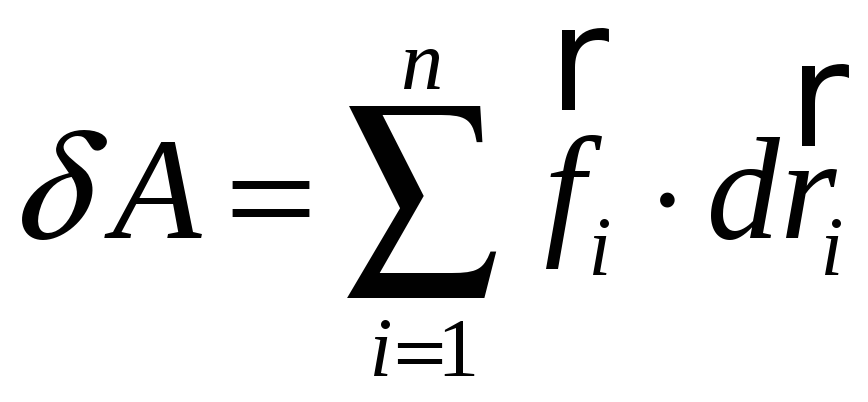
Заменим в Ур.(2) суммы

(3)

Для конечных перемещений

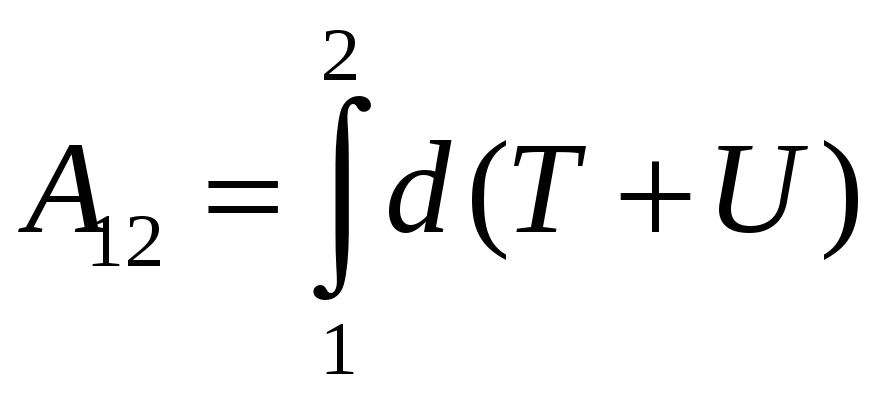
- работа неконсервативных сил. Итак, изменение полной энергии равно работе неконсервативных сил. Если консервативные силы отсутствуют, из (3) имеем или

(4)

Это количественная формулировка закона сохранения полной механической энергии. Механические системы, в которых действуют только консервативные силы, называются консервативными. Закон сохранения энергии связан с однородностью времени. Закон сохранения и превращения энергии: энергия никогда не исчезает и не появляется вновь, она превращается из одного вида в другой.

Столкновение тел

Рассмотрим абсолютно упругий удар двух тел. В этом случае тела не деформируются, а полная кинетическая энергия тел до удара равна энергии после соударения. При упругом ударе выполняются законы сохранения импульса и энергии. Удар называется центральным, если тела до удара двигаются вдоль прямой, проходящей через их центры масс. Пусть имеется два шара с массами . Они двигаются со скоростями до соударения и после удара.

Рис.

Из закона сохранения импульса

Закон сохранения энергии

Имеем систему из двух уравнений. Неизвестные величины – скорости .

Преобразуем систему уравнений.

Находим скорости шаров после столкновения

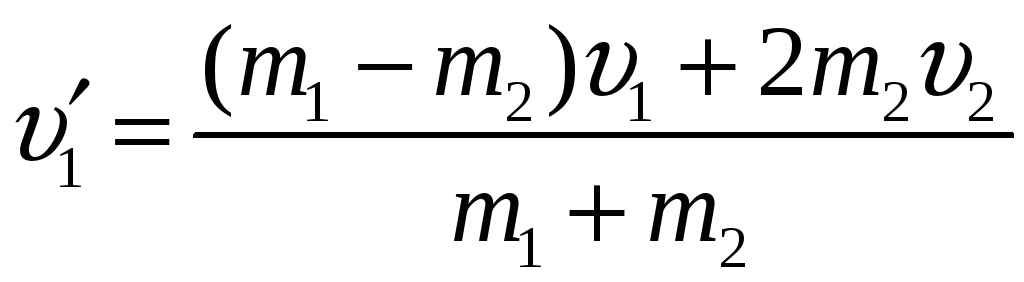
Анализ скоростей зависит от соотношения масс шаров, соотношения и значений начальных скоростей. Например, если , т.е. шары имеют одинаковую массу, получаем

и .

Шары обменялись скоростями. Если до удара, то после удара .

Абсолютно неупругий удар. После удара шары двигаются вместе. Закон сохранения импульса

находим скорость

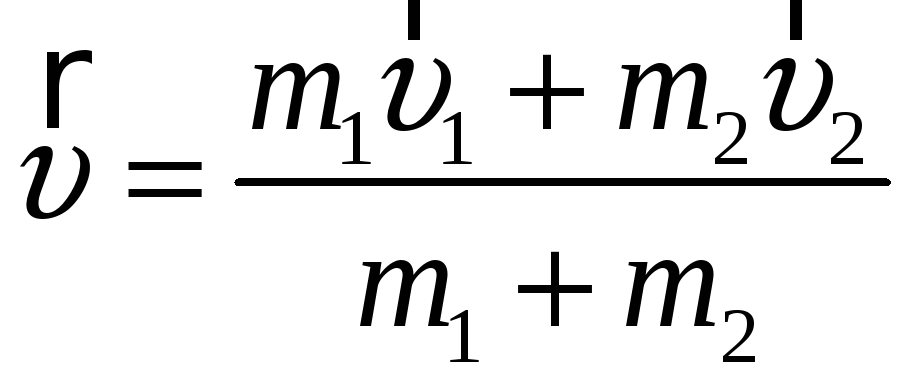
Часть кинетической энергии шаров переходит в тепловую энергию и другие виды энергии.