Физика / 1 ЭЛЕМЕНТЫ МАТЕМАТИКИ

ЭЛЕМЕНТЫ МАТЕМАТИКИ

Пусть имеется функция . Определим производную

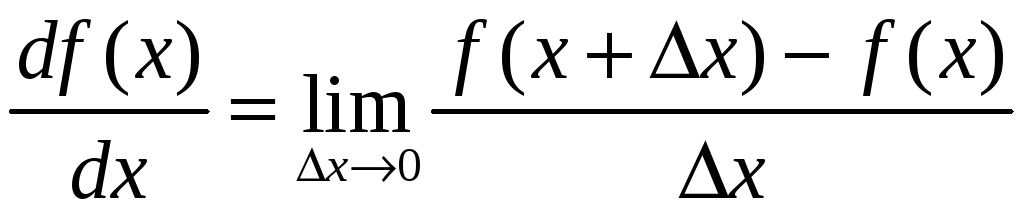
Обозначение производной функции по аргументу :

, ,

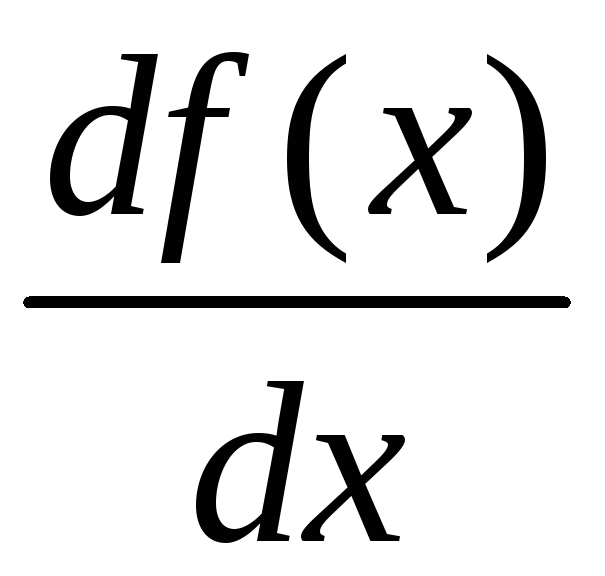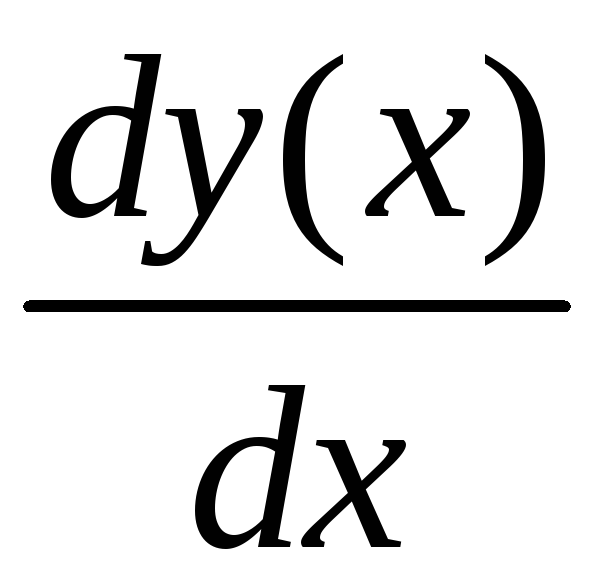Если функция зависит от нескольких переменных, например, , можно определить частную производную по одной независимой переменной.

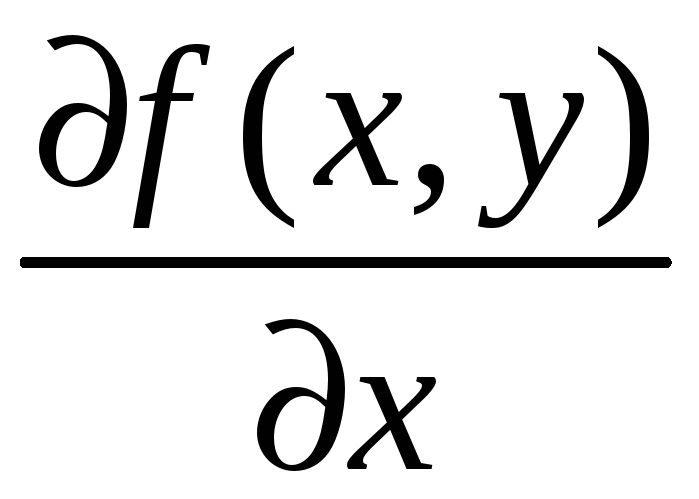и т.д.

Операция, обратная к дифференцированию, называется интегрированием. Определим неопределенный интеграл

, где - первообразная, - постоянная.

Соотношение 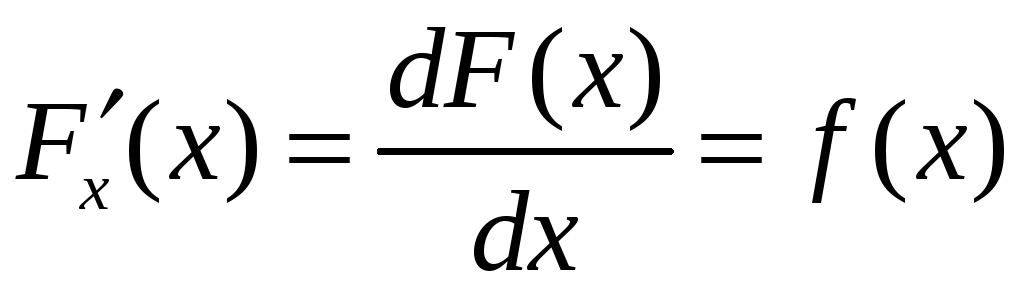определяет связь функции и её первообразной.

Определенный интеграл определяется как предел интегральной суммы. , , .

Интегральная сумма возникает в результате разбиения интервала, который определяет область изменения независимой переменной . Определим число , Оно называется диаметром разбиения. Предел интегральных сумм обозначается . Определенный интеграл

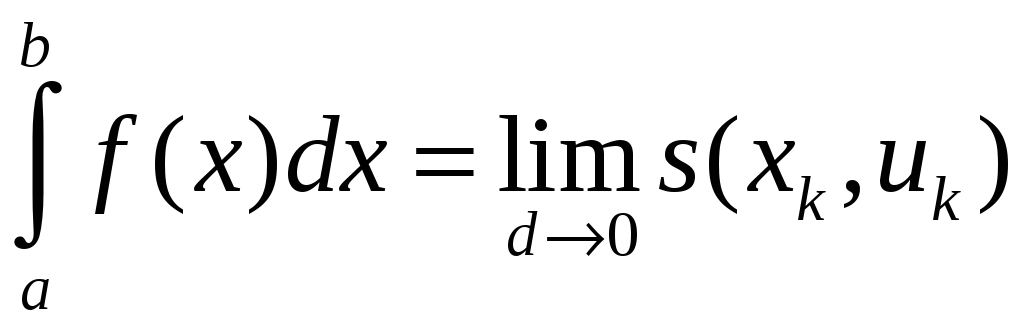. Связь с первообразной

.

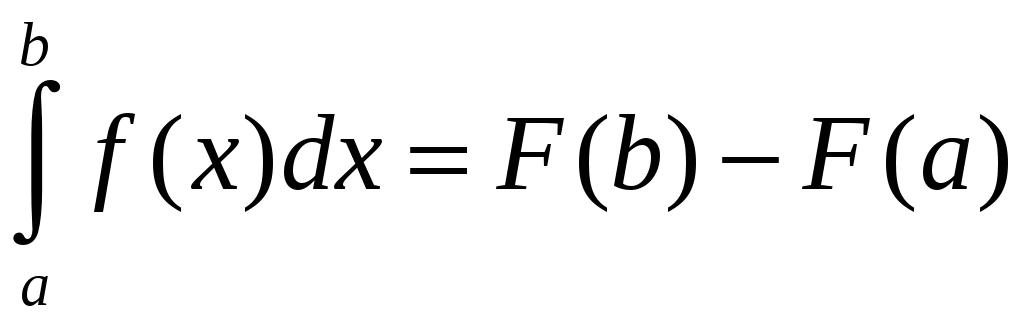ВЕКТОРЫ

Определим вектор как направленный отрезок прямой линии. Обозначается

, где - орты декартовой системы координат. Они определяют положительное направление координатных осей , соответственно. Величины называются компонентами вектора . Компонента вектора – это проекция вектора на соответствующую ось. Компоненты могут быть числами, в этом случае вектор является постоянным, его значение не зависит от координат точки пространства, в котором находится начало вектора. Компоненты вектора могут зависеть от координат точки, т.е. они являются скалярными функциями: . Аналогично и для остальных компонент. В этом случае имеем дело с векторной функцией, которая изменяется от точки к точке. Вектор характеризуется величиной и направлением. Величина вектора или его модуль определяется . Модуль любого орта равен единице. Среди векторов выделим вектор, который называется радиус-вектор. Он обозначается

.

Его начало находится в начале координат, конец в точке с координатами . Т.о. этот вектор задает координаты точки.

Над векторами допустимы следующие операции:

Сложение векторов.

Сумма двух векторов , где компоненты вектора равны

, ,

Разность двух векторов.

, где компоненты вектора равны , ,

Сумму и разность двух векторов можно графически представить в виде соответствующей диагонали параллелограмма, построенного на этих векторах.

Произведение векторов.

А) скалярное , где - угол между векторами и . Результат скалярного произведения есть число, либо скалярная функция.

Б) векторное произведение

=

Определитель раскрывается по первой строке.

Направление вектора определяется по правилу правого винта.

Построим плоскость, содержащую векторы и . Если необходимо совместим их начала путем параллельного переноса. Восстановим перпендикуляр к плоскости в точке, где начинаются векторы и . Если в векторном произведении вектор вращать к вектору против часовой стрелки вокруг оси, перпендикулярной плоскости, в которой лежат исходные векторы, то направление движения правого винта покажет направление вектора .

Вектор можно умножать на число или скалярную функцию. При этом все компоненты вектора умножаются на соответствующий множитель.

Деление вектора на вектор не определено.

Два вектора равны только в том случае, когда равны их соответствующие компоненты.

Орты координат определяются следующим образом

если и

для всех . .

Единичный вектор направлен вдоль соответствующей оси.

Определим поверхностный интеграл

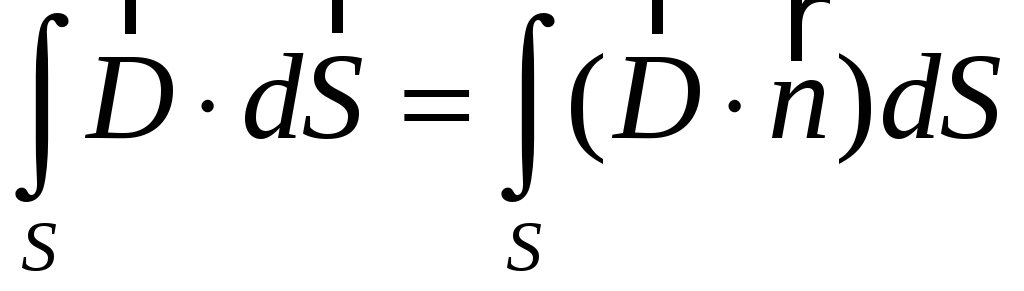
Элемент поверхности , где - нормаль к данному элементу; - площадь элемента поверхности.

МАТРИЦЫ, ОПРЕДЕЛИТЕЛИ.

Матрицей называется совокупность элементов, имеющих определенную структуру. Двумерные матрицы имеют вид

Она содержит элементов. Для квадратной матрицы можно ввести определитель, который есть сумма слагаемых, каждое из которых есть произведение из различных элементов матрицы. При этом в каждом слагаемом содержится по одному элементу из каждой строки и столбца. Например, для матрицы размерности определитель равен:

. Определитель третьего порядка, который определяет векторное произведение двух векторов, приведен выше.

КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ

Если задача обладает симметрией, удобно работать не в декартовых переменных, а в криволинейных. Наиболее широко используемые переменные: сферические и цилиндрические. Они связаны с симметрией сферы и цилиндра, соответственно. Определим эти переменные и их связь с декартовыми переменными. При определении всегда имеется декартовая система координат.

Сферические переменные: . Где - расстояние от начала декартовой системы координат до точки наблюдения; - угол между осью и радиус-вектором точки наблюдения; - угол между осью и проекцией радиус-вектора на плоскость или .

Связь с декартовыми переменными. , ,

.

Цилиндрические переменные: . - полярные переменные. Их можно определить в плоскости , используя проекцию радиус вектора на данную плоскость, либо в плоскости, параллельной и пересекающей ось в точке . Связь с декартовыми переменными: , , .

КОМПЛЕКСНЫЕ ПЕРЕМЕННЫЕ

Рассмотрим комплексное число . Где - действительные числа, а - мнимая единица. Мнимая единица удовлетворяет соотношению . Звездочка означает комплексное сопряжение. Число называется комплексно сопряженным числу . Их произведение есть величина действительная. Широко используется показательная форма записи комплексного числа.

, где и .

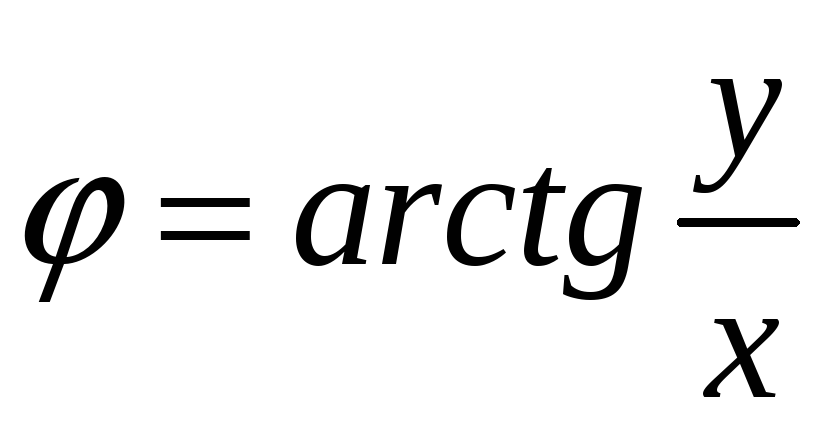Формула Эйлера .