Физика / 4 МЕХАНИКА ТВЕРДОГО ТЕЛА

МЕХАНИКА ТВЕРДОГО ТЕЛА.

Момент инерции. Кинетическая энергия.

Тело называется - абсолютно твердым, если расстояние между любыми двумя его точками остается постоянным. Момент инерции (МИ) – мера инертности твердых тел при вращении (аналог массы при прямолинейном движении). Момент инерции тела относительно оси для системы точечных масс равен сумме произведений масс материальных точек на квадрат их расстояний до оси:

(1)

Для протяженного непрерывного тела: . (2)

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой параллельной оси определяется теоремой Штейнера. Теорема Штейнера:

. (3)

- момент инерции относительно произвольной оси ; - момент инерции тела относительно параллельной оси, проходящей через центр масс тела; слагаемое равно произведению массы тела на квадрат расстояния между осями.

Пример: Найти МИ для полого тонкостенного цилиндра радиуса , высотой с постоянной поверхностной плотностью относительно оси цилиндра.

Рис.

Поскольку тело обладает симметрией, элемент площади цилиндрической поверхности равен: , т. к. . Масса этого элемента равна

. Масса полого цилиндра равна боковой площади цилиндра на плотность . Тогда момент инерции, согласно (2) равен

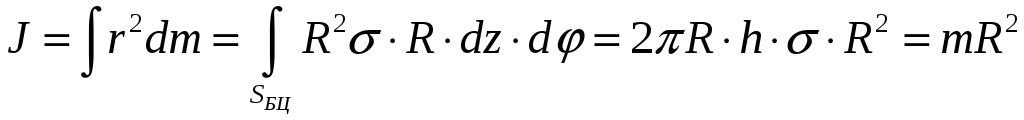
Моменты инерции некоторых симметричных тел вычислены и имеются в справочниках.

Найдем кинетическую энергию вращающегося тела. Для наглядности представим, что тело – это системы материальных точек с массами и расстояниями от оси вращения . Поскольку точки неподвижны друг относительно друга, они вращаются с одинаковой угловой скоростью.

Кинетическая энергия вращения относительно оси равна

.

Итак, кинетическая энергия вращения вокруг неподвижной оси :

. (4) - момент инерции системы относительно неподвижной оси . Аналогичное выражение можно получить для протяженного тела. В этом случае - момент инерции тела относительно неподвижной оси . Кинетическая энергия тела, движущегося по плоскости:

,

где - момент инерции тела относительно оси, проходящей через его центр масс. Она складывается из двух частей: энергии поступательного движения и энергии вращательного движения. Это следует учитывать, когда тело, например шар или цилиндр, скатывается по наклонной плоскости.

Момент силы, уравнение динамики вращательного движения.

Момент силы относительно неподвижной точки:

. (1)

Модуль , где - плечо силы. Угол - угол между векторами и . Начало координат выбрано в неподвижной точке.

Момент силы относительно неподвижной оси , , скалярная величина, равная проекции вектора момента силы на ось . Поскольку данная величина является проекцией, то она не зависит от выбора точки на оси. Пусть ось совпадает с направлением момента силы, тогда , т.е. величина момента силы равна её проекции на ось .

Найдем работу, совершаемую при вращении тела. Под действием силы тело может вращаться вокруг неподвижной оси. Приложенную силу разложим по компонентам

Рассмотрим тангенциальную составляющую. Она приводит к вращению тела вокруг оси. Остальные компоненты вызывают деформацию тела. Тангенциальная компонента лежит в плоскости, перпендикулярной оси вращения. Для удобства будем считать, что , тогда и . Ось вращения и ось совпадают.

При повороте на угол точка тела переместиться на величину . Элементарная работа, совершаемая при этом:

.

Так как и .

(2)

Работа при вращении идет на изменение кинетической энергии тела.

в силу закона сохранения энергии. Изменение энергии равно:

(3)

сравнивая соотношения (2) и (3), имеем

делим обе части равенства на . Учитывая определения и , получаем

. (4)

Это уравнение динамики вращательного движения. Когда ось совпадает с одной из главных осей твердого тела и проходит через его центр инерции,

. (5)

Уравнения (4) и (5) – это уравнения динамики вращательного движения твердого тела.

Момент импульса, закон сохранения.

Момент импульса относительно неподвижной точки определяется как

(1)

где - импульс тела. Модуль момента импульса равен

Момент импульса относительно неподвиждной оси – это скалярная величина, равная проекции момента импульса относительно неподвижной точки, лежащей на данной оси. Он не зависит от выбора этой неподвижной точки. Пусть ось совпадает с направлением момента импульса. Найдем момент импульса относительно оси для системы материальных точек:

(2)

Полученное выражение продифференцируем по времени

(3)

Это ещё одно представление уравнения динамики вращательного движения. Сравнивая выражение (2) с определением момента силы Ур.(4) , замечаем, что

(4)

Это уравнение можно записать в векторном виде:

. (5)

В замкнутой системе момент внешних сил равен нулю, тогда

или

Момент импульса сохраняется. Закон сохранения момента импульса.

Деформации твердого тела.

Абсолютно упругая деформация. В этом случае тело принимает изначальную форму после прекращения внешних воздействий. Пластическая деформация – изменение формы сохраняется после снятия внешних сил. Рассмотрим упругие деформации. Имеем прямой цилиндр длиной и диаметром . Сила (растяжение или сжатие) действует вдоль оси цилиндра. Возникает упругая деформация, которая определяет силу упругости.

Водится величина, называемая напряжением:

(1)

где - площадь поперечного сечения цилиндра. Пусть - нормаль к поверхности . Если , то называется нормальным напряжением. Для напряжение тангенциальное. Количественная мера деформации - относительная продольная деформация:

. (2)

Где - изменение длины стержня. Для поперченного растяжения (сжатия) относительного изменение диаметра определяет поперечную деформацию.

(3)

Экспериментально обнаружена связь:

(4)

- коэффициент Пуассона.

Связь напряжения и относительной продольной деформации (удлинение):

, (5)

где - модуль Юнга. Он равен отношению приложенного напряжения к вызванному им относительному удлинению:

Найдем связь силы и величины изменения длины стержня. Для этого выразим относительную продольную деформацию через модуль Юнга и величину силы:

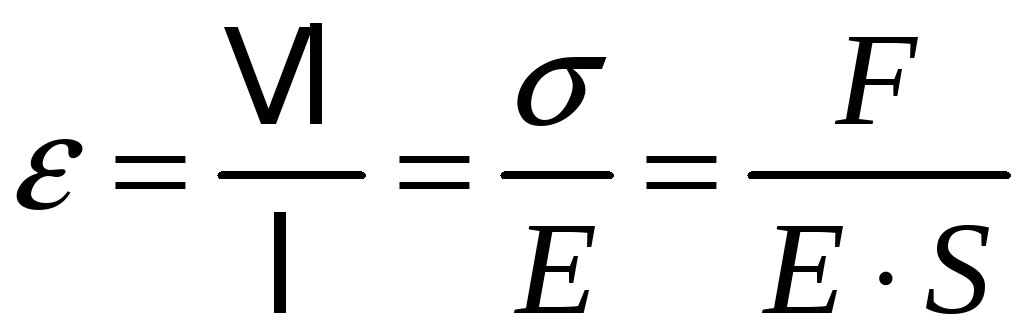. Отсюда

(6)

Ур. (6) - закон Гука. - коэффициент упругости.

Потенциальная энергия упруго растянутого стрежня равна работе