fizicheskij_praktikum_zubkov

Лабораторная работа № 4

ИЗМЕРЕНИЕ АРТЕРИАЛЬНОГО ДАВЛЕНИЯ КРОВИ МЕТОДОМ КОРОТКОВА

Цель работы: 1) научиться измерять кровяное давление с помощью тонометра по методу Короткова; 2) изучить особенности движения крови в сосудистой системе; 3) уяснить физические законы, которым подчиняется движение крови.

Приборы и принадлежности: манометр точный мембранный ММТ-3, фонендоскоп, пневматический нагнетатель, компрессорная манжета для взрослых пациентов, тонометр электронный.

4.1. Теоретическая часть

Кровь – это реальная жидкость, которой присущи все свойства

считать, что перемещение одних частей жидкости относительно других не связано с возникновением сил трения. Жидкость, в которой внутреннее трение (вязкость) полностью отсутствует, называется идеальной.

Это уравнение Бернулли, где r – плотность жидкости, g –

ускорение свободного падения, u – скорость движения жидкости, Р – статическое давление, rgh – гидростатическое давление, обусловленное высотой столба жидкости. Несмотря на то, что это уравнение было получено для идеальной жидкости, оно хорошо выполняется для реальных жидкостей, внутреннее трение в которых не очень высоко.

При выводе этого уравнения нигде не используется предположение о несжимаемости жидкости, поэтому оно справедливо и для сжимаемых жидкостей:

61

Вдоль одной и той же линии тока при стационарном течении идеальной жидкости в поле тяготения Земли сумма гидростатического, гидродинамического и статического давлений есть величина постоянная.

Если трубка тока имеет переменное сечение(как это имеет место в кровеносной системе человека), а ось трубки горизонтальна ( h = const), то уравнение Бернулли принимает вид:

Отсюда видно, что давление Р больше там, где скорость u меньше, и наоборот. С другой стороны, из уравнения неразрывности струи следует,

что скорость меньше там, где больше сечение трубки s1u1 = s2u2 .

Значит, в широких частях трубки давление максимально, а в узких – минимально. Этот результат является следствием второго закона Ньютона. (Объясните!)

В медицине важным методом исследования состояния организма и, в частности состояния сердечно-сосудистой системы, является измерение

желудочков сердца. Диастолическое – давление крови на стенку артерии во время диастолы(расслабления) желудочков. Разность между этими давлениями называют пульсовым давлением. Среднее давление – интегральная величина, представляющая собой среднее всех мгновенных значений кровяного давления за время сердечного цикла:

Указанная величина – эквивалент затрат энергии на поддержание реальных значений кровяного давления в течение сердечного цикла.

В клинике применяется косвенный способ измерения артериального давления. Он заключается в ,томчто измеряют давление, которое необходимо приложить снаружи, чтобы сжать артерию до прекращения в ней тока крови. Это давление весьма близко к давлению крови в артерии. Наиболее распространен метод измерения артериального давления по . Н

62

Короткову, основанный на выслушивании звуков, озникающих при прохождении крови через сжатую манжетой артерию. Появление в ходе декомпрессии (уменьшения сжатия) первого звука, улавливаемого фонендоскопом, соответствует максимальному систолическому давлению крови в артерии, просвет которой раскрывается после предшествовавшего сдавливания манжетой. Звуки исчезают, когда деформация просвета артерии будет полностью устранена. Это соответствует диастолическому (минимальному) давлению крови.

Данные звуковые феномены впервые описал 1905в году врач Н. Коротков. Метод Короткова очень удобен и доступен, однако он уже не удовлетворяет всем требованиям тонких клинических и физиологических исследований геодинамики. В частности, он не позволяет измерять среднее давление крови в артериальном русле, а именно оно– важнейший параметр гомеостаза.

Для быстрого стравливания воздуха из манжеты после измерения необходимо повернуть регулятор нагнетателя против стрелки до упора.

Измерения давления и пульса с помощью электронного тонометра выполняются в соответствии с инструкцией прибора.

63

4.3. Экспериментальная часть

На рис. 4.1 представлены механический и электронный тонометры.

Рис. 4.1. Два типа тонометров (электронный и механический)

для определения кровяного давления

1. Без физической нагрузки, в спокойном состоянии пациента произвести измерение давления тем и другим тонометрами. Посчитать пульс и сравнить с показаниями электронного тонометра. Данные занести в табл. 4.1.

произвести с интервалом в2 минуты 5 - 7 раз для определения времени релаксации сердечно-сосудистой системы.

64

4.Результаты измерений занести в табл. 4.1.

5.На одном график построить релаксационные кривые верхнего и нижнего давления Р(t).

6.Построить релаксационную кривую пульса n(t).

Котчету представить:

•таблицу с результатами измерений давления и пульса;

•график релаксации верхнего и нижнего давлений Pв (t) ; Pн (t) ;

•график релаксации пульса n(t).

Контрольные вопросы

1.Природа артериального давления.

2.Объяснить физические основы метода Короткова.

3.Какие явления происходят в большом круге кровообращения? Объяснить модель кровообращения.

4.Свойства жидкости. Вязкость жидкости. Закон Ньютона для жидкости.

5.Условия ламинарного и турбулентного движения жидкости. Критерий Рейнольдса.

6.Понятия идеальной жидкости, линии тока, трубки тока. Условия неразрывности струи.

7.Вывести уравнение Бернулли, объяснить его физический смысл.

65

Лабораторная работа № 5

ОБОРОТНЫЙ МАЯТНИК

Цель работы: определение ускорения свободного падения методом оборотного маятника; оценка результатов измерений.

Приборы и материалы: оборотный маятник, секундомер.

5.1. Теоретическая часть

Гармоническим осциллятором называется система, совершающая колебание, описываемое дифференциальным уравнением вида:

66

где y0 – начальная фаза колебаний.

Из этого решения следует, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой w0 и

физического маятника.

67

68

физического маятника рассмотрим математический маятник, у которого вся масса сосредоточена в одной точке– центре масс. Тогда выражение

маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.

нерастяжимой невесомой нити длиной l , и колеблющаяся под действием силы тяжести.

убывает до некоторого минимального значения, а затем снова возрастает (гармоническая зависимость). Качественный вид зависимости изображен

69

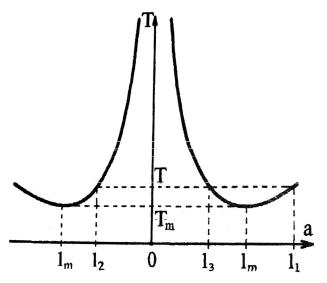
соответствующие положению точки подвеса маятника справа и слева от его центра масс.

Рис. 5.2. Зависимость периода колебаний физического маятника от длины

Возвращаясь к измерению ускорения свободного падения методом оборотного маятника, обратим внимание на , точто основным его достоинством является необходимость измерения только двух величин:

расстояния между ребрами опорных призм( l1 + l2 = l) и периодов колебаний маятника в положенииl1 и в«перевернутом» положении l2

таком, что l1 ¹ l2 .

Маятник может колебаться в вертикальной плоскости, опираясь нижним ребром одной из призм на закрепленную на массивном штативе опорную площадку. Перемещая призмы по стержню, можно отыскать такие две сопряженные точки подвеса ( O1 , O2 ), что при подвешивании оборотного

маятника за одну или другую точку период колебаний останется неизменным.

70