Сила сопротивления разгону

Сила сопротивления разгону воз­никает вследствие затрат энергии на раскручивание вращающихся частей двигателя и трансмиссии, а также колес при движении автомобиля с ускорением.

Сила сопротивления разгону, Н:

где G — вес автомобиля, Н; g — ус­корение силы тяжести, м/с²; δ_вр — коэффициент учета вращающихся масс автомобиля; j — ускорение ав­томобиля, м/с².

Мощность, кВт, затрачиваемая на разгон:

Зависимости силы сопротивления разгону Р_и и мощности N_И, необходимой для преодоления этого сопротивления, от скорости автомобиля v представлены на рис. 3.20.

Коэффициент учета вращающихся масс

Этот коэффициент учитывает дополнительное сопротивление разгону автомобиля, вызванное раскручиванием вращающихся ча­стей двигателя, трансмиссии и колес.

Коэффициент учета вращающихся масс показывает, во сколь­ко раз мощность, затрачиваемая на разгон автомобиля, больше мощности, не

обходимой для установившегося движения:

где J_м — момент инерции маховика; u_T, η_тр — передаточное число и КПД трансмиссии; J_сум — суммарный момент инерции всех ко­лес автомобиля.

Коэффициент учета вращающихся масс для автомобиля с пол­ной нагрузкой можно приближенно рассчитать по формуле

47

где u_к, u_д — передаточные числа основной и дополнительной ко­робок передач.

Условие равномерного движения при отсутствии буксования ведущих колес записывается в вид

3.12. Уравнение движения автомобиля

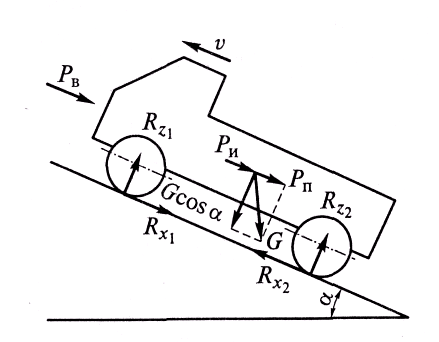
Для вывода уравнения движения рассмотрим разгон автомоби­ля на подъеме (рис. 3.21).

Спроецируем все силы, действующие на автомобиль, на по­верхность дороги:

(3.19)

Подставим в формулу (3.19) касательные реакции дороги R_x1, и R_x2,

объединим члены с коэффициентом сопротивления каче­нию ƒ и члены с ускорением j и, принимая во внимание соотно­шения ƒ(R_z2+R_z1 ) = Р_K, и j_k1 + j_k2 = j_k , а также коэффициент уче­та вращающихся масс, получим уравнение движения автомобиля в общем виде:

Или

(3.20)

Уравнение движения автомобиля выражает связь между дви­жущими силами и силами сопротивления

Рис. 3.21. Схема сил, действую­щих на автомобиль на подъеме

движению. Оно позволяет определить режим движения автомобиля в любой момент.

Так, например, при установившемся (равномерном) движе­нии

Из уравнения (3.20) следует, что безостановочное движение автомобиля возможно только при условии

р

^гв-

Данное неравенство связыва­ет конструктивные параметры ав­томобиля с эксплуатационными факторами, обусловливающими сопротивление движению. Одна­ко оно не гарантирует отсутствия буксования ведущих колес. Безо­становочное движение автомоби­ля без буксования ведущих колес возможно лишь при соблюдении условия

Условия равномерного движения при отсутствии буксования ведущих колёс записывается в виде

3.13. Силовой баланс автомобиля

Представим уравнение движения автомобиля в следующем виде: (3.21)

В такой форме оно называется уравнением силового баланса автомобиля и выражает соотношение между тяговой силой на ве­дущих колесах и силами сопротивления движению.

На основании уравнения (3.21) строится график силового ба­ланса, позволяющий оценивать тягово-скоростные свойства ав­томобиля.

При построении графика силового баланса (рис. 3.22) сначала строят тяговую характеристику автомобиля. Затем наносят зави­симость силы сопротивления дороги от скорости. Если коэффи­циент сопротивления дороги — постоянная величина, то указан­ная зависимость представляет собой прямую линию, параллель­ную оси абсцисс, а при непостоянном коэффициенте сопротив­ления дороги — кривую параболической формы. После этого от кривой, характеризующей силу сопротивления дороги, отклады­вают вверх значения силы сопротивления воздуха при различных скоростях движения. Полученная зависимость