
Physics_II
.pdf
(r )
где p
|
1 |
|
|
q |
|
|
|
q |
|
|
|
|
|
|
|
|
q |
|
||||
|
|
|
|
r |
e |
|
|
e |
|
|
N |
|
|
|||||||||
|
|
|
|
i |
(1 |
|
i |
r |
) |
|
i |
|
r |
|
qi ri |
|
|
i |
||||
4 |
|
|
|
|
4 |
|
r |
4 |
|
r 2 |
4 |
|
r |
|||||||||
|
0 |
i |
r |
|
|
r |
0 |
|
0 |
i 1 |
|
|
0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
qi ri - дипольный электрический момент системы зарядов.
i1
p er , (*)
4 0r2
|
|
|
|
|
|
|
|
|
|
|
В случае диполя, |
где всего два заряда, получаем p ql . В общем случае вектор |
p |
||||||||
зависит от выбора начала координат O , но если qi 0, то не зависит. |
|
|||||||||
Доказательство. Возьмем два начала координат: O и O' . |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
ri |
' ri |
b ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p' qi ri |
' qi (ri |
b) qi ri |
b qi |
p bq |
|
|
||||
Если q 0 , |
|
|
|
|
|
|
|
|
||
то p' p , но если |
q 0 , то p' p . |
|
|
|||||||
Формула (*) |
соответствует |
разложению |
потенциала в |
ряд по степеням 1/ r . Если |
||||||
q 0 , то главный член – первый, и поле вдали от системы соответствует полю точечного
заряда ( ). Если , а 0 , то главный член – второй, и поле определяется как поле
p
1/ r q 0
2
диполя (1/ r ) (см. формулу (*) в §6). Если же и q 0 , и p 0 , то главным будет
следующий член в разложении, соответствующий «квадруполю» и пропорциональный 1/ r 3 .
Если и он обращается в ноль, то поле соответствует «октуполю» (1/ r 4 ).
Глава 2. Элементы векторного анализа.
§1. Градиент.
Если в каждой точке задано значение какой-то физической величины, то говорят, что задано поле этой величины. Оно может быть скалярным или векторным, например,
температура или напряженность поля.
Пусть задано скалярное поле (x, y, z) . Введем понятие градиента этой величины:
grad |
i |
j |
k |
|
|
|
|
|
|
|
x |
y |
|
z |
Приращение функции |
|
|
|
|
при смещении на отрезок dl |
dx i |
dy j |
dz k равно |
11

d |
dx |
dy |
dz |
|
|
|
|
|
|
|
|
||
|
x |
y |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
«набла» |
|
|
|
|
|
|
|
|
||
Введем дифференциальный векторный оператор |
i |
j |
k , тогда |
||||||||||
x |
y |
z |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
grad .
*****************************************************************************
Об операторах, функциях и функционалах.
Оператор – это действие, сопоставляющее функции функцию, например, если оператор sin
применить к функции f (x) , то получим новую функцию sin( f (x)) .
Функция ставит в соответствие числу число: y x3 , числу x 2 соответствует y 8 .
Существует еще одно понятие - функционал. Он ставит в соответствие функции число,
5
например, A f (x)dx - каждой функции f (x) соответствует число A .
1
*****************************************************************************
§2. Поток вектора.
Рассмотрим течение жидкости. Задано векторное поле скоростей v (r ) . Объем жидкости, протекающей через поверхность за 1 секунду, называется потоком жидкости через эту поверхность. Найдем его. Разобьем поверхность S на
участки S . За время t через S пройдет объем V ,
равный объему призмы: V S v t cos .
высота призмы
Поток Ф V / t S v cos . Считая S
|
|
получим dФ dS v cos v |
dS . Мы ввели вектор |
поверхности в данной точке. Тогда Фv |
|
|
v |
dS . |
|
|
(S ) |
|
равным бесконечно малому dS ,
dS , направленный по нормали к
Аналогично можно ввести поток любого вектора a через поверхность S :
Фa |
|
|
andS |
|
a |
dS |
|
||
|
(S ) |
|
(S ) |
|
Поток – величина скалярная (алгебраическая). Его знак зависит от выбора направления |
||||
|
|
|
|
|
нормали n к поверхности. В случае замкнутых поверхностей n |
всегда направлен наружу. |
|||
12

Потоку можно дать геометрическую интерпретацию. Изобразим |
|
|
|
||||||||||||||
векторное поле системой линий, построенных так, что в каждой точке |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
густота линий |
равна |
|
a |
в этой точке (например, |
силовые |
линии |
|
|
|
||||||||
электрического |
поля). |
Число |
пересечений |
этими |
линиями |
площади |
S , равное |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N a S cos an S , есть поток вектора a через площадку S . |
|
|
|||||||||||||||
Для учета знака будем при остром угле считать число пересечений с плюсом, а при |
|||||||||||||||||
|
|
|
|
|
|
N 3 . |
|
|
|
|
|
|
|
|
|||
тупом – с минусом. В |
нашем примере |
Если |
выбрать |
|
n |
направленным в |
|||||||||||
противоположную сторону, то N 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рассматривая целую поверхность, получим Ф Ni |
N N . |
|
|
||||||||||||||
Для замкнутой поверхности пересечения изнутри наружу имеют знак плюс, наоборот – |
|||||||||||||||||
минус. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если линии непрерывны, то в замкнутую поверхность они входят столько же раз, |
|||||||||||||||||
сколько и выходят из нее. Поэтому Ф 0 . Если же |
|
|
|
|
|
|
|
|
|||||||||
они могут оканчиваться или начинаться внутри, то |
|
|
|
|
|
|
|
|
|||||||||
Ф Nнач Nоконч. Знак Ф зависит от того, |
каких |
|
|
|
|
|
|
|
|
||||||||
больше. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§3. Дивергенция. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пусть задано векторное поле скоростей жидкости v . Возьмем |
в |
|
|||||||||||||||
окрестности точки Р замкнутую поверхность площадью S . Если в объеме |
|
||||||||||||||||
внутри этой поверхности нет ни стоков, ни |
истоков, то |
Ф 0 . |
Если |
|
|||||||||||||
Ф 0 , значит, есть стоки или истоки. Ф определяет соотношение стоков и |
|
||||||||||||||||
истоков. Ф /V |
дает |
среднюю |
удельную |
(на |
1 м3) мощность источников в объеме V . |
||||||||||||
Устремляя V |
к нулю, |
т.е. стягивая объем |
в точку Р, получаем удельную мощность |
||||||||||||||
источников в точке Р. Назовем ее дивергенцией (или расхождением). |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
lim |
Фv |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
div v |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
V |
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
lim |
Ф |
lim |
1 |
|
|
|||
Аналогично для любого векторного поля: |
div a |
a |
|
|
adS . Интеграл |
||||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
V 0 |
V |
V 0 V |
( S ) |
|
|||
берется по любой замкнутой поверхности, окружающей точку Р.
div a - скалярная функция координат. Она численно равна плотности точек, в которых
начинаются (+) или оканчиваются (-) линии вектора a . Найдем ее выражение в декартовой системе координат.
13

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим поток вектора |
|
a |
через грани 1 |
и 2 (заднюю и |
|
||||||||||||||||||||||||||||
переднюю) |
параллелепипеда. Нормаль в замкнутой поверхности |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ox . |
|
|
|
|
|||||||||
всегда направлена наружу. Поэтому n2 Ox, n1 |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax |
|
|
|
|
|
|
|
ax . |
|
|
|||||||||
Найдем проекции a |
на n1 |
и n2 : |
|
|
an |
; |
|
|
an |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
||
|
Ф a |
y z ; |
|
Ф a |
|
y z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2 |
x2 |
|
|
|
2 |
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф Ф (a |
x |
a |
x |
) y z ax x y z ax V |
|
|||||||||||||||||||||||||||
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|||||||
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Аналогично найдем потоки через левую и правую, а также через верхнюю и нижнюю |
|||||||||||||||||||||||||||||||||
грани параллелепипеда. В итоге получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
x |
|
|
|
ay |
|
|
|
|
a |
z |
|
|
|
|
|
|||||||
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
x |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
||||||||||
|
|
|
|
|
lim |
Ф |
|
|
|
a |
|
|
|
ay |
|
a |
|
|
|||||||||||||||
|
|
|
|
div a |
|
|
|
a |
|
|
|
|
|
x |
|
|
|
|
|
|
z |
|
|||||||||||
|
|
|
|
V |
|
|
x |
|
|
y |
z |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
V 0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Используя векторный оператор , получим div a |
a (скалярное произведение). |
||||||||||||||||||||||||||||||||
§4.Теорема Остроградского-Гаусса. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зная |
дивергенцию |
в |
каждой |
точке, |
можно |
|
найти поток вектора a |
через любую |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
заданную |
поверхность. |
Рассмотрим |
|
|
вектор |
|
скорости жидкости v . Тогда |
div a dV - |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dV |
|
|
|
|
|
|
|
|
|||||
мощность источников в объеме |
|
dV , |
|
а |
|
div v |
|
- суммарная мощность источников в |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(V ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
объеме V . Она должна равняться потоку, вытекающему из объема через поверхность S : |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dV |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
v |
dS |
div v |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
(S ) |
|
|
|
|
|
|
|
|
(V ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это же верно для любого a : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
dV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
a dS |
div a |
|
|
|
- это теорема Остроградского-Гаусса. |
|||||||||||||||||||||||||||
|
(S ) |
|
|
(V ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Левый интеграл берется по замкнутой поверхности S , а правый – по объему внутри S .
14
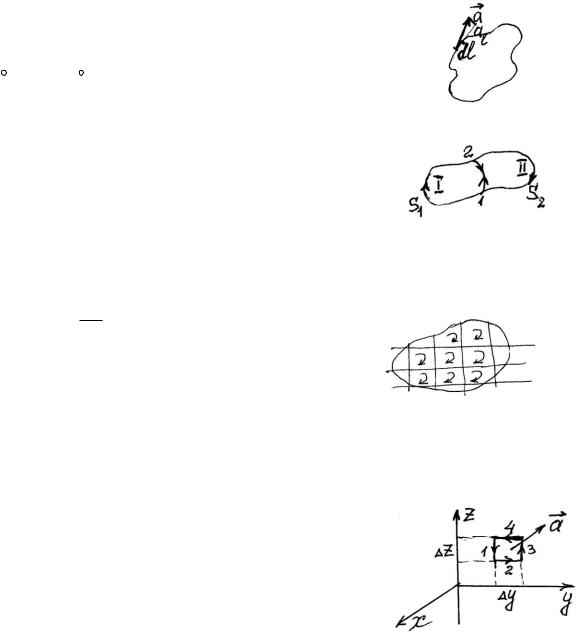
§5.Циркуляция и ротор.
Назовем циркуляцией вектора a по замкнутому контуру Г (гамма)
|
|
|
al dl . |
величину a |
dl |
|
|
( Г ) |
|
|
( Г ) |
Циркуляция обладает аддитивностью, т.е. С С1 С2 . Выполнение этого равенства легко увидеть из рисунка, так как по общему участку в циркуляциях С1 и С2 проходим в противоположных направлениях, т.е. знаки будут разными.
Аддитивность циркуляции позволяет ввести понятие удельной циркуляции, т.е.
рассмотреть отношение циркуляции к площади обтекаемой поверхности.
Рассмотрим lim Ca . Эта величина зависит не только от
S 0 S
точки, но и от ориентации площадки. Можно показать, что существует такой вектор (назовем его ротором), что
|
|
|
|
lim |
C |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(rot a) |
|
|
|
|
, где вектор |
n - нормаль к площадке S . (В зарубежной литературе |
|||||||||||||||||||||||||||||||||||||||||
n |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
S 0 |
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
вместо обозначения “rot” используется “curl”). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Найдем проекцию ротора на ось х. Циркуляция равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
С С2 |
С3 С4 С1 |
ay |
2 |
y az |
3 |
z ay |
y az z |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(az |
|
|
az ) y (ay |
ay |
|
) z |
a |
z |
y z |
|
|
ay |
|
z y |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
y |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
3 |
|
|
1 |
|
|
|
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
a |
z |
|
|
ay |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
y z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
z |
|
|
ay |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(rot a) |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
x |
a |
z |
|
|
|
|
|
|
|
|
|
|
ay |
|
a |
x . |
|||||||||||
Аналогично получим: |
(rot a) |
y |
|
|
|
|
|
|
|
|
|
и |
(rot a) |
z |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это формулы для нахождения проекций вектора rot a на декартовы оси координат. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
|
k |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Используя оператор набла, можно написать |
|
rot a |
|
|
|
|
|
|
|
|
|
a |
|
||||||||||||||||||||||||||||||||||
|
|
x y |
z |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax |
|
ay |
az |
|
|
|
|
|
|
||||
15

|
|
|
|
|
|
Обобщим результаты: grad ; div a |
a ; rot a |
a . |
|
||
Отметим, что в других системах координат (сферической, цилиндрической и т.п.) все |
|||||
эти формулы имеют другой вид, и оператор не используется. |
|
|
|
|
|
§6.Теорема Стокса. |
|
|
|
|
|
|
|
|
Г , |
||
Зная rot a в каждой точке поверхности, можно найти циркуляцию a |
по контуру |
||||
ограничивающему эту поверхность. Для этого разобьем поверхность на малые S . Ввиду |
|||||
|
|
S |
|
|
|
малости, их можно считать плоскими. Поэтому С (rot a)n |
rot a S . |
|
|||
|
|
Тогда C Ci rot ai |
|
|
|
a |
dl |
Si , а при стремлении Si к нулю, получим
|
|
rot a |
dS - теорема Стокса. |
|
( Г ) |
( S ) |
Здесь S - это поверхность, ограниченная контуром Г . |
||
§7.Оператор набла. |
|
|
grad ; |
|
|
|
|
|
div a |
a ; |
|
|
|
|
rot a |
a . |
|
- оператор, действующий на |
все |
величины, стоящие |
справа |
от него. Получим |
||||||||||
некоторые формулы, действуя с оператором формально. |
|
|
|
|
|
|
|
|||||||
grad ( ) ( ) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
div( a) ( a) a a |
grad a |
div a |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
div grad ( ) |
x2 y2 |
|
|
|
||||||||||
|
z2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
оператор Лапласа |
|
|
|||||
rot grad ( ) 0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
0 , так как смешанное произведение равно объему призмы, |
||||||||||||
div rot a |
( a) |
|||||||||||||
который обращается в ноль, если два вектора из трех совпадают. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rot rot a |
( a) ( a) |
2 a |
grad div a |
a |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь мы использовали формулу: a |
(b |
c) b(a |
c) c(a |
b). |
|
|||||||||
Отметим, что вывод этих формул не является строгим. Он только дает возможность предположить результат, для уверенности их нужно проверять строгой математикой.
16

Из формулы div rot a
теореме Стокса интеграл от контуром Г .
0 |
|
следует, что rot a не имеет источников. Именно поэтому в |
ротора по поверхности определяется только ограничивающим ее
§8.Циркуляция и ротор электростатического поля.
Электростатические силы консервативны, т.е их работа по замкнутому контуру равна
нулю. Отсюда следует:
|
|
|
|
|
|
E dl |
|
rot E dS |
0 по любой поверхности S , ограниченной контуром Г . Из |
||
( Г ) |
|
|
(S ) |
|
|
|
|
|
|
0 |
|
этого следует: |
|
rot E |
- первое уравнение электростатического поля. |
||
§9.Теорема Гаусса и дивергенция электростатического поля.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассчитаем поток E через сферу радиуса r для поля точечного заряда q : |
||||||||||||||||||||||||||||||||||
|
|
q |
|
|
|
dS |
|
|
|
q |
|
|
|
|
4 r 2 |
|
|
q |
|
|
|
|
|
|
|
|||||||||
EdS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
r |
2 |
|
4 |
|
|
|
r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Это количество линий, начинающихся (или при q 0 заканчивающихся) на заряде q . |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значит, поток E через |
любую замкнутую поверхность, внутри которой в любой точке |
|||||||||||||||||||||||||||||||||
находится точечный заряд q , равен q / 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пусть внутри замкнутой поверхности находится |
|
N точечных зарядов. Тогда поток |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
N |
|
|
|
q |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
||||||||||||
вектора E будет равен: |
ФE |
EdS |
|
( Ei )dS |
|
qi |
|
|
i 1 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
i 1 0 |
|
|
|
|
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Это теорема Гаусса: поток |
E через |
замкнутую |
|
|
поверхность равен |
алгебраической |
||||||||||||||||||||||||||||
сумме зарядов, заключенных внутри этой поверхности, деленной на 0 . |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dq / dV : |
Если заряд распределен непрерывно, т.е. задана плотность заряда (r ) |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
dV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
EdS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С другой стороны, из теоремы Остроградского-Гаусса |
следует, что |
поток E через |
||||||||||||||||||||||||||||||||
поверхность равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
EdS |
|
div E |
dV |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
(S ) |
|
|
|
|
|
(V ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Это справедливо для любой поверхности, поэтому |
|
div E |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
0 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |

Это дифференциальная форма теоремы Гаусса (2-е уравнение Максвелла для
электростатики).
§10. Вычисление полей с помощью теоремы Гаусса.
1. Бесконечная заряженная плоскость. |
||
Пусть поверхностная |
плотность заряда на плоскости равна |
|
dq / dS . |
Построим |
параллелепипед, так что плоскость |
рассекает его |
пополам. Из |
соображений симметрии следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
вектор E в любой точке направлен перпендикулярно плоскости (от нее, если 0 ). Тогда |
||||||||||||
поток через боковые грани равен нулю. |
|
|
|
|
|
|
|
|
|
|||
Ф Q / |
|
|
0 2ES S / |
|
|
E |
|
|
(поле однородно) |
|||
0 |
0 |
|
|
|||||||||
E |
|
|
|
|
|
2 0 |
||||||
|
|
|
|
|
|
|
|
|||||
2. Бесконечный заряженный цилиндр. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
Пусть линейная плотность |
заряда равна dq / dl . |
||||||||
|
|
Построим цилиндрическую поверхность такого вида, проходящую |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
через исследуемую точку. Из симметрии следует, что E направлен |
||||||||||
|
|
|
r в плоскости, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
по |
перпендикулярной оси цилиндра, причем |
E |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
зависит только от расстояния до оси r . Запишем теорему Гаусса: ФE Q / 0 . Поток через
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
верхний и нижний круги |
равен нулю (т.к. линии |
E их не |
«протыкают»). |
На боковой |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поверхности E параллелен dS . |
E 2 rh h / |
|
|
E |
|
1 . |
||||||||||
|
q |
|
EdS E |
|
dS E 2 rh , |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
2 0 |
|
r |
|||||||
|
|
|
|
площадь |
|
|
|
|
|
|
||||||
боковой пов ти
2. Объемно заряженный шар.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из симметрии следует, что E в любой точке направлен по радиусу и модуль E зависит |
||||||||||||||||||||||
только от r . Мысленно проведем сферу радиусом r с центром в точке О. |
|
|
||||||||||||||||||||
|
|
1) r R |
|
|
|
|
|
|
|
|
|
|
4 r 3 / |
|
|
r . |
||||||
|
q |
|
EdS E |
|
dS E 4 r 2 |
E 4 r 2 |
|
E |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||
|
0 |
|
|
|
|
|
|
|
3 |
|
|
3 0 |
||||||||||
|
|
|
|
|
|
|
|
площадь |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
пов ти |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
сферы |
|
|
|
|
|
|
|
|
||||
Поскольку |
3Q |
|
, то E |
Q |
|
|
|
r |
|
(при r R ). |
|
|
|
|
|
|
|
|||||
4 R3 |
4 |
0 |
|
|
R3 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

2) r R , |
E 4 r 2 Q / |
|
E |
Q |
|
1 |
|
0 |
|
|
|
|
|||
4 |
|
|
r 2 |
||||
|
|
|
|
|
|||
|
|
|
|
0 |
|
||
|
|
|
|
|
|
|
|
При r R обе формулы дают один и тот же результат.
Глава 3. Электрическое поле в диэлектриках.
§1. Полярные и неполярные молекулы.
Диэлектрики – вещества, не способные проводить электрический ток. Идеальных диэлектриков не существует, но реальные диэлектрики проводят ток в 1020 раз хуже, чем
проводники.
Если диэлектрик внести в электрическое поле, то это поле и сам диэлектрик претерпевают изменения. Это происходит потому, что в состав атома входят отрицательные электроны и положительное ядро. Всякая молекула имеет суммарный заряд, равный нулю. Ее размеры малы, поэтому на макроскопических расстояниях ее поле является полем диполя,
«плюс» которого находится в «центре тяжести» положительного заряда, а «минус» - в
«центре тяжести» отрицательного.
У симметричных молекул ( Н2 ,О2 и т.п.) центры плюсов и минусов совпадают, и
дипольный момент равен нулю. Такие молекулы называются неполярными. У
несимметричных молекул ( СО2 , NH3 и т.п.) центры плюсов и минусов сдвинуты относительно друг друга. Такие молекулы обладают собственным дипольным моментом и называются полярными. В электрическом поле полярные и неполярные молекулы ведут себя по-разному. В неполярных под действием поля плюсы и минусы раздвигаются, и молекула
|
|
|
|
|
|
приобретает дипольный момент, величина которого пропорциональна |
Е : |
p 0 E , |
( |
||
|
|
|
|
|
|
называется поляризуемостью |
молекулы). При снятии поля p исчезает. |
Говорят, |
что |
||
неполярная молекула ведет себя в поле, как упругий диполь. |
|
|
|
|
|
|
|
|
|
|
|
Полярные молекулы в |
поле Е поворачиваются, стремясь |
встать |
по полю. |
Их |
|
дипольный момент не зависит от Е , поэтому говорят, что полярная молекула ведет себя в поле, как жесткий диполь. Строго говоря, раздвижение плюсов и минусов под действием поля также происходит, но этот эффект пренебрежимо мал в сравнении с влиянием поворота молекул.
19

§2. Поляризация диэлектрика.
В отсутствие внешнего поля дипольный момент диэлектрика равен нулю. Под
действием Е диэлектрик поляризуется, т.е. его дипольный момент становится отличным от
нуля. В качестве характеристики степени поляризации диэлектрика естественно взять дипольный момент единицы объема. Если поле или диэлектрик неоднородны, т.е. степень
|
|
|
|
|
|
|
|
1 |
|
|
|
поляризации в разных точках разная, то назовем поляризацией величину P |
|
|
|
|
p , где |
||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
V V |
||
|
|
|
|
|
V . |
|
|
|
|
|
|
суммирование ведется по физически бесконечно малому объему |
|
P |
называется |
||||||||
поляризацией. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У изотропных диэлектриков любого типа P 0 E , где |
f (E) |
- безразмерная |
|||||||||
величина, называемая диэлектрической проницаемостью диэлектрика. |
|
|
|
|
|
|
|
||||
Проверим размерности: [ p] Кл м , [P] |
Кл |
[ |
|
E] , как и должно быть. |
|||||||
|
0 |
||||||||||
|
м2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
§3. Поле внутри диэлектрика.
Заряды, входящие в состав молекул, называются связанными. Под действием Е они
могут только немного смещаться от положения равновесия, но не могут покинуть молекулу.
Заряды, не входящие в состав молекул, называются сторонними. Поле в диэлектрике является
суперпозицией полей, созданных связанными и сторонними зарядами:
Емикро Естор Есвяз .
Микроскопическое поле сильно меняется в пределах межмолекулярных расстояний.
Поскольку связанные заряды еще и движутся, то оно меняется и со временем. В качестве характеристики поля возьмем поле, усредненное по физически бесконечно малому объему:
|
|
|
|
|
|
|
|
|
Е |
Емикро Естор |
Есвяз |
Е0 |
Е'. Здесь |
Е - |
макроскопическое поле, |
Е0 - |
|
|
|
|
|
|
|
|
|
|
внешнее, поле связанных зарядов здесь и далее будем обозначать Е'. Поляризация P - |
||||||||
|
|
|
|
|
|
|
|
|
макроскопическая величина, поэтому в формулу P 0 E |
входит именно Е . В вакууме |
|||||||
|
|
|
|
|
|
|
|
|
E E0 |
Eстор . |
|
|
|
|
|
|
|
§4. Объемные и поверхностные связанные заряды.
Когда диэлектрик не поляризован, то ' 0 и
' 0 . При поляризации ' и иногда |
' отличаются |
от нуля. Из рисунков видно, что |
на границах |
20 |
|
