Физика (Электричество)_ЛЕКЦИИ И ВОПРОСЫ / OF4_6_Проводники Электрическая ёмкость_mini

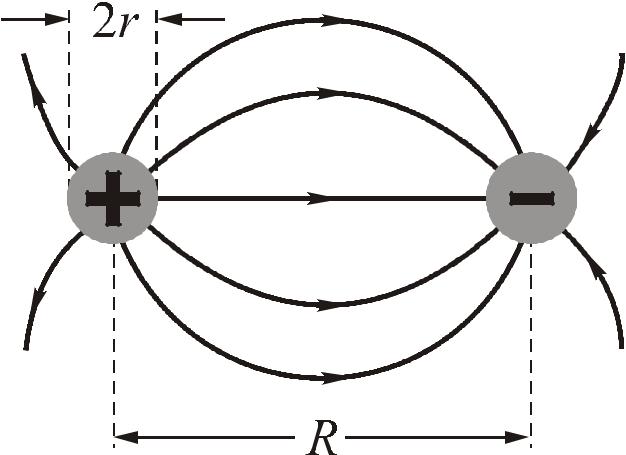
Электрическое поле двухпроводной линии

Ёмкость двухпроводной линии на каждую единицу длины:

r

Ёмкость сферы радиуса a

(Capacitance of sphere, radius a)

C = 4πε0εa

Ёмкость круглого диска радиуса a

(Capacitance of circular disk, radius a)

C = 8ε0εa

Ёмкость двух контактирующих сфер радиуса a

(Capacitance of two spheres, radius a, in contact)

C = 8πε0εa ln 2

4.6.6. Размерность абсолютнойтной диэлектрической проницаемостити вв СИСИ

Понятие электрической ёмкости используют в системе СИ для определения единицы измерения абсолютной диэлектрической проницаемости ε0:

Отсюда единица ε0 в СИ – 1 ( Ф·м)·м–2 = 1 Ф·м–1 («фарад на метр»).

4.6.7. Энергия заряженногоного конденсатора

Допустим, что на поверхности проводника находится заряд q, а потенциал равен φ. Перенесём на поверхность проводника дополнительный элементарный заряд dq. Работа, выполненная внешними силами по перенесению этого заряда из бесконечности на поверхность проводника, равняется:

δAвнешн = dqϕ

Так как заряд dq мал, то его перенесение на поверхность заряженного проводника лишь незначительно изменит его потенциал на dφ, а связь между ними:

dq = Cdϕ

Энергия заряженного конденсатора

В учебнике – опечатка!

Тогда работа внешних сил δАвнешн:

δAвнешн = Cdϕϕ = Cϕdϕ

Работа Авнешн внешних сил по перенесению всех элементарных

зарядов dq на поверхность проводника:

= ∫Cϕdϕ = 1 Cϕ2

ϕ 2

Работа Авнешн, выполненная внешними силами по перенесению всех зарядов dq на поверхность проводника, идёт на приращение потенциальной энергии Eп заряженного проводника Авнешн = +∆Eп. Следовательно, потенциальная энергия заряженного проводника:

Энергия заряженного конденсатора

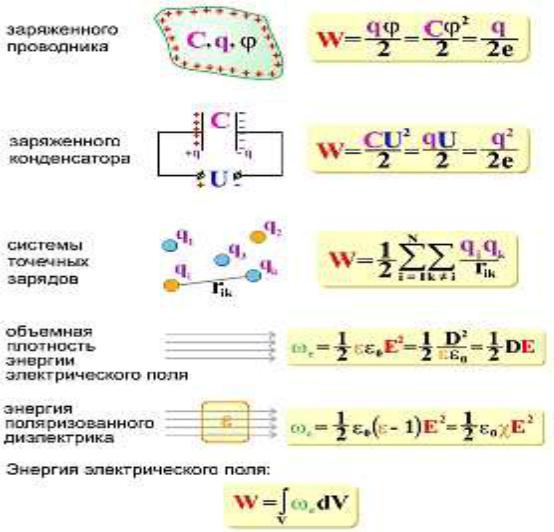
Потенциальная энергия