
Fizika_i_khimia_beta-prevrascheny
.pdf
Кривая 3 получена по формуле (42) и соответствует изотропному испусканию частиц.
Рис. 22. Расчетные спектры энергии отдачи ядер для некоторых случаевугловой корреляции β– – ν]. (Принято, что масса ядра равна 100 а.е.м., Еβmax = 2 МэВ):
1 — θ = 0°; 2 — θ = 180°; 3 — изотропное распределение, полученное для восьми различных углов
Кривые, представленные на рис. 22, характеризуются непрерывным распределением энергий от нулевых до максимально возможных значений.
Максимальная энергия отдачи дочернего ядра представляет интерес в практическом аспекте, поскольку именно этот параметр позволяет прогнозировать возможность разрушения молекулы в состав которой входит β–-излучатель. Поскольку дочернее ядро получает максимально возможную энергию отдачи Eотд.max при нулевой энергии антинейтрино, то для вычисления Eотд.max удобно использовать выражение, полученное после преобразования формулы (42) с учетом E~ν = 0 : :
Eотд.max |
= 536 |
Eβmax |
[Eβmax +1.02], |
(45) |
|
||||
|
|
M |
|
|
51

где Eβmax — максимальная энергия β-излучения, МэВ; М — масса ядра отдачи, а.е.м.
Пример 4. Вычислить максимальную энергию отдачи свободного ядра 3Не, возникающего после β–-распада 3Н (Eβmax ≈ 0.02 МэВ).
Eотд.max = 536 0.302[0.02+1.02] = 3.72 эВ.
Для сравнения, энергии разрыва химической связи в соединениях Т2 и ТН равны 1.8 эВ и 0.9 эВ, соответственно. Отсюда следует, что β-распад трития, входящего в состав этих молекул, может вызвать их разрушение.
1.10.2.Эффект ядерной отдачи после захвата орбитального электрона
Возможность существования эффекта ядерной отдачи при захвате орбитального электрона не столь очевидна, как при β+ и β–-рас- падах, поскольку s-орбитали имеют сферическую форму. В связи с этим возникает вопрос: будет ли наблюдаться эффект отдачи при захвате симметричного электронного облака? Ответ на этот вопрос зависит от того, сопровождается ли захват облака излучением какихлибо частиц. Если частицы не излучаются, то отдачи быть не может.
Как известно, захват электрона ядром всегда сопровождается испусканием нейтрино, обладающим импульсом и энергией. Следовательно, в соответствии с законом сохранения импульса, дочернее ядро, образовавшееся в результате захвата электрона, должно испытывать отдачу. Величину энергии отдачи при K-захвате вычисляют по формуле:
ER |
= 536 |
Eν2 |
, |
(46) |
|
M |
|||||
|
|
|
|
где Eν — энергия нейтрино, МэВ; М — масса ядра отдачи, а.е.м.
Пример 5. Вычислить энергию отдачи свободного ядра 7Li, возникающего в результате K-захвата в ядре 7Ве (Еν= 0.864 МэВ).
ER = 536 0.8642 = 57.2 эВ. 7
52

В 1955 году был выполнен эксперимент по измерению энергии отдачи дочернего ядра после захвата электрона. При выборе объекта исследований потребовалось соблюдение ряда условий:
―доминирующим каналом распада должен быть K- (или L-) захват;
―дочернее ядро должно возникать только в основном состоянии, иначе энергия отдачи дочернего ядра окажется аддитивной вели-
чиной, зависящей от угла между направлениями вылета нейтрино и γ-квантов.
Одним из ядер, удовлетворяющих этим условиям, оказался изотоп 37Ar. Ядро 37Ar в 92 % случаях испытывает K-захват и в 8 % случаях — L-захват. Энергия нейтрино равна 0.816 МэВ.
Ожидаемая энергия отдачи дочернего ядра 37Cl:
ER = 536 0.81637 2 = 9.65 эВ.
Экспериментально было получено значение, равное 9.63±0.06 эВ, которое хорошо согласуется с расчетом. Таким образом был подтвержден эффект ядерной отдачи после захвата электрона.
53

Р а зд е л 2
ВЗАИМОДЕЙСТВИЕ β-ИЗЛУЧЕНИЯ
С ВЕЩЕСТВОМ
Электроны или позитроны, испущенные ядром, вовлекаются в процессы взаимодействия с веществом, приводящие к ионизации окружающей среды и к возникновению электромагнитного излучения. Конечным результатом прохождения бета-частиц через вещество является частичная или полная потеря β-частицей исходной кинетической энергии, а также отклонение от первоначального направления, называемое рассеянием28. Сначала рассмотрим эффекты рассеяния.
2.1.ОСОБЕННОСТИ ДВИЖЕНИЯ β-ЧАСТИЦ В ВЕЩЕСТВЕ. ТРАЕКТОРИЯ И ПРОБЕГ
Под пробегом частицы в каком-либо веществе понимают толщину слоя этого вещества, которую может пройти частица с энергией Е0 до полной остановки при условии, что направление ее движения перпендикулярно поверхности слоя.
Понятие пробега связано с траекторией движения частицы. Например, для тяжелых частиц, движущихся прямолинейно, понятия траектории и пробега совпадают. Бета-частицы движутся в окружающей среде по очень сложным непрямолинейным траекториям, проходя при этом расстояние в 1.5–4 раза превышающее толщину поглощающего слоя, поэтому понятия траектории и пробега для них не совпадают (рис. 23).
28 Различают упругое и неупругое рассеяние. Рассеяние называется упругим, если сохраняется сумма кинетических энергий взаимодействующих частиц. Любое другое рассеяние называется неупругим.
54
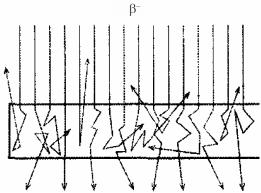
Рис. 23. Схематическое представление рассеяния параллельного пучка электронов в веществе
Неупорядоченный характер движения бета-частиц обусловлен многочисленными упругими столкновениями бета-частиц с электронами. Поскольку сталкивающиеся частицы имеют равные массы, электрон способен терять значительную долю своей энергии при единичном соударении. Кроме того, столкновения частиц одинаковых энергий сопровождаются обратным рассеянием.
Криволинейная траектория β-частиц вызывает сложности при определении длины пробега частиц в веществе. Так, например, две β-частицы с одинаковыми начальными энергиями могут пройти в веществе одинаковое расстояние, но в итоге окажутся в разных точках поглощающего вещества, поскольку их траектории существенно отличаются по форме.
Из вышесказанного следует, что использование единиц длины (мм, см) для оценки пробега электронов в веществе нецелесообразно. Вместо этого на практике пробег β-частиц обычно оценивают в единицах поверхностной плотности вещества (мг/см2).
Предположим, имеется источник β-излучения с начальной интенсивностью N0. Если на пути β-частиц помещать поглотители из одного и того же материала, но с возрастающей поверхностной плотностью d (что эквивалентно возрастанию толщины), то уменьшение интенсивности потока β-частиц приближенно можно описать выражениями близкими к экспоненциальному закону:
N ≈ N0e−μd d |
(47) |
или |
|
N ≈ N0e−μl l , |
(48) |
|
55 |

где N0 — число бета-частиц, излучаемых в отсутствии поглотителя; N — число бета-частиц, прошедших сквозь данный поглотитель; μd — коэффициент пропорциональности, называемый массовым коэффициентом поглощения, см2/г; d — поверхностная плотность поглотителя, г/см2; μl — коэффициент пропорциональности, называе-
мый линейным коэффициентом поглощения, см–1; l — толщина по-
глотителя, см.
Если толщина слоя поглотителя выражается в линейных единицах (см), то следует использовать линейный коэффициент поглощения (уравнение 48). Если толщина слоя поглотителя выражается в единицах поверхностной плотности (г/см2), то используется массовый коэффициент поглощения (уравнение 47).
Массовый и линейный коэффициенты поглощения связаны между собой следующим выражением:
μd = μρl ,
где ρ — плотность вещества.
Для характеристики пробега в веществе β-частиц с данной максимальной энергией используют два параметра:
―слой полного поглощения (Rмакс.);
―слой половинного поглощения (d1/2).
Слой полного поглощения или максимальный пробег β-частиц
(Rмакс.) — это минимальная толщина поглотителя, преодолев которую пучок β-частиц полностью теряет исходную интенсивность. Иначе говоря, скорость счета препарата за поглотителем становится равной скорости счета фона.
Имеется ряд эмпирических выражений, с помощью которых можно оценить величину слоя полного поглощения бета-частиц определенных энергий в конкретном веществе (обычно в качестве поглотителя рассматривают фольгу из алюминия).
Например:
Еβ =1.39Rмакс0.6 . b2 −4ac при Еβ макс.<0.15 МэВ; Eβ =1.92Rмакс0.725. при 0.15 МэВ< Еβ макс.<0.8 МэВ;
Eβ =1.85R +0.245 при Еβ макс. >0.8 МэВ.
При использовании этих выражений величина R получается в г/см2.
56
Слой половинного поглощения (d1/2) — это минимальная толщина поглотителя, после преодоления которой исходная интенсивность пучка β-частиц снижается вдвое.
Значения массового и линейного коэффициентов поглощения, а также толщины слоев полного и половинного поглощения зависят от максимальной энергии бета-частиц и от материала поглотителя.
В табл. 5 в качестве иллюстрации приведены данные для алюминиевого поглотителя.
Таблица 5
Максимальные пробеги Rмакс., слои половинного ослабления d1/2 и массовые коэффициенты ослабления μd β-излучения в алюминии
Еβmax, МэВ |
μd, см2/г |
d1/2, мг/см2 |
Rмакс., мг/см2 |
0.01 |
6930 |
0.1 |
0.16 |
0.05 |
866 |
0.8 |
3.9 |
0.10 |
385 |
1.8 |
14 |
0.50 |
40 |
17.5 |
160 |
0.80 |
19 |
37 |
310 |
1.00 |
13 |
53 |
410 |
1.50 |
7.1 |
97 |
670 |
2.00 |
5.0 |
140 |
950 |
2.50 |
4.0 |
173 |
1220 |
Слой половинного поглощения связан с коэффициентами поглощения простыми выражениями, которые получаются из (47) и (48)
при наложении следующих условий: при d = d1/2 |
N = |
1 |
N0 . |
|||||
2 |
||||||||
Таким образом: |
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
1 |
N |
|
≈ N0e−μd d1/2 |
|
|
|
|
2 |
0 |
|
|
|
||||
|
|
|
|
|
|
|||
и |
|
|
|
|
|
|
||
|
1 |
N |
|
≈ N0e−μl l1/2 . |
|
|
|
|
2 |
0 |
|
|
|
||||
|
|
|
|
|
|
|||
Отсюда следует:
d1/2 ≈ |
ln 2 |
≈ |
0.693 |
; |
(49) |
μd |
μd |
57

d1/2 |
≈ |
ln 2 |
≈ |
0.693 |
. |
(50) |
|
|
|||||
|
|
μl |
μl |
|
||
На рисунках 24 (а, б) слою полного поглощения соответствуют отрезки Rмакс., слою половинного поглощения — отрезки d1/2.
По наклону прямолинейного участка кривой поглощения в полулогарифмических координатах (рис. 24, б) находят коэффициенты ослабления μd или μl:
μd = tg φ
или
μl = tg φ,
где φ — угол наклона прямой.
Рис. 24. Кривые ослабления бета-излучения:
а — в линейных координатах; б — в полулогарифмических координатах. Пунктирной линией показана экспоненциальная зависимость
При анализе кривых ослабления следует обратить внимание на то, что экспоненциальный закон хорошо совпадает с экспериментальными данными только в области средних значений толщины поглотителя. В области малых и больших значений наблюдается заметное отступление от экспоненциальной зависимости (рис. 24, б, пунктирная линия).
Метод изучения ослабления интенсивности β-излучения может быть использован для идентификации радионуклидов, поскольку слои полного и половинного поглощения (для конкретного поглотителя), в сочетании с периодом полураспада, являются качественны-
58
ми характеристиками β-частиц. Метод имеет ограничения — надежные результаты могут быть получены при излучении бета-частиц одного сорта и отсутствии сопутствующего гамма-излучения. Если эти условия не выполняются, то необходимо использовать более точный метод β-спектрометрии.
Пример |
6. |
|
Какая доля бета-частиц, |
излучаемых 32Р |
(Eβmax = |
||||||||||||||||
= 1.71 Мэв), поглощается в слое слюды толщиной 5.21 мг/см2, если |
|||||||||||||||||||||
слой половинного ослабления равен 62 мг/см2? |
|
|
|||||||||||||||||||
По формуле (49) находим массовый коэффициент ослабления: |
|||||||||||||||||||||
|
|
|
|
|
|
μ |
|
≈ |
ln 2 |
= |
0.693 |
|
= 0.011 см2 /г. |
|
|
||||||
|
|
|
|
|
d |
d |
|
62 мг/см2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1/2 |
|
|
|
|
|
|
|
|
|
|
||
Поскольку |
|
|
N |
|
|
|
|
|
N |
|
|
N |
= e−μd d , |
|
|||||||
|
|
|
|
|
|
+ |
|
|
|
= |
1 и |
|
|
находим |
|||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
N0 погл. |
|
N0 непогл. |
|
|
N0 непогл. |
|
|
||||||||
долю поглощенных бета-частиц: |
|
|
|
|
|
|
|||||||||||||||
|
N |
|
|
|
|
|
N |
|
=1−e−μd d |
=1−e−0.011 5.21 =1−0.94 = 0.06. |
|||||||||||
|
|
|
≈1 |
− |
|
|
|
||||||||||||||
N0 |
N0 |
||||||||||||||||||||
|
погл. |
|
|
|
|
непогл. |
|
|
|
|
|
|
|
|
|
||||||
2.2.ВЗАИМОДЕЙСТВИЕ, СОПРОВОЖДАЕМОЕ ВОЗБУЖДЕНИЕМ И ИОНИЗАЦИЕЙ АТОМОВ
Отметим, что ионизация и появление электромагнитного излучения, как правило, происходят одновременно. Однако, для лучшего понимания этих процессов, рассмотрим закономерности их появления раздельно.
Бета-частицы, проходя сквозь вещество, вызывают возбуждение или ионизацию атомов, причем оба процесса имеют примерно равную вероятность и объединяются под общим названием ионизационные потери энергии. Механизм ионизационных потерь энергии бета-частицами заключается в передаче дискретных порций энергии орбитальным электронам окружающего вещества при единичных актах неупругого рассеяния.
Количественным выражением ионизационных потерь энергии
служит удельная ионизация |
dE |
. |
2 |
|
||
|
|
|
(МэВ/гсм |
|
или МэВ/см), от- |
|
|
|
|||||
|
|
dx иониз. |
|
|
|
|
ражающая потерю энергии на единицу пути.
59

Теория ионизационных потерь электронов была разработана Н.Бором, а также Х. Бете29 и Ф. Блохом30.
Ионизационные потери энергии электронами релятивистских энергий оценивают с помощью формулы:
|
|
|
|
|
|
|
|
− |
dE |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
dx иониз. |
|
|
||
|
2πn e4 |
|
|
0.511 β2 E |
кин. |
|
|
|
|
|
|
||
= |
e |
|
ln |
|
|
|
−ln 2 (2 |
(1−β2 ) −1+β2 )+(1−β2 ) |
, |
(51) |
|||
0.511 β |
2 |
|
2 |
|
2 |
||||||||
|
|
|
2I |
|
(Z ) (1−β ) |
|
|
|
|
|
|
||
где I (Z) = 13.5Z — средний ионизационный потенциал атомов поглощающего вещества, эВ; е — заряд электрона, Екин. — кинетическая энергия электрона, ne — число электронов в 1 см3 вещества, β — от-
ношение скорости движения электрона (v) к скорости света |
|
β = |
v |
|||
|
|
. |
||||
|
||||||
|
|
|
|
|
c |
|
Проанализируем выражение (51). Величина |
dE |
|
для дан- |
|||
|
||||||
dx |
иониз. |
|
|
|
|
|
ного поглотителя зависит от кинетической энергии частицы и заряда частицы.
Согласно (51), при энергиях бета-частиц до 1 МэВ (β→0), ионизационные потери энергии уменьшаются. При энергии бета-частиц
порядка 1.02 МэВ (удвоенная масса покоя |
электрона), величина |
|||
dE |
достигает минимального значения. |
По мере возрастания |
||
|
|
|
||
|
||||
|
dx иониз. |
|
|
|
энергии β-частиц и, особенно, при скоростях близких к скорости све-
та (β→1), величина |
dE |
|
испытывает релятивистский подъем. |
|||
|
||||||
dx иониз. |
|
|
|
|
||
Графическое изображение зависимости |
dE |
|
от энергии |
|||
|
||||||
|
|
|
dx |
иониз. |
|
|
β-частиц представлено на рис. 25.
29Ханс Альбрехт Бете (2 июля 1906 г. — 6 марта 2005 г.), американский астрофизик, лауреат Нобелевской премии по физике (1967).
30Феликс Блох (23 октября 1905 г. — 10 сентября 1983 г.) — швейцарский физик, работал главным образом в США. Лауреат Нобелевской премии по физике за 1952 год (совместно с Эдвардом Пёрселлом).
60
