3.Функции: определение, способы задания. Основные элементарные функции, их графики. Свойство функций – монотонность, ограниченность. Обратная функция, сложная функция.

Переменная величина у называется функцией другой переменной величины х если указано правило или закон f ,который позволяет каждому значению переменной х из множества Dx ставится в соответствие одно вполне определенное значение у. Если у есть функция от х в смысле указанного определения то у=f(x) (1). При этом переменная х называется аргументом функции , у - самой функции, f - закон или правило соответствия между у и х. Dx называется областью определения функции или областью допустимых значений аргумента, а множество Ey – это множество всех значений функции соответствующее всем возможным значениям «х» из области Dx . В матане рассматриваются 3 способа задания функции (одного аргумента)

1)табличный

2)графический

3)аналитический – функция задается формулой.

Основными элементарными функциями являются:

1)степенная (y=x²)

2)показательная(y=a^x)

3)логарифмическая

4)тригонометрическая

5)обратная

Монотонно возрастающие и монотонно убывающие функции.

1. y=f(x) называется возрастающей в своей области определения если в этой области большему значению аргумента соответствует большее значение функции. График возрастающей функции всегда идет снизу вверх направо.

2. y=f(x) называется убывающей во всей своей области определения если в этой области большему значению аргумента отвечает меньшее значение функции.

Сложная функция – это функция от функции.

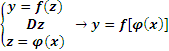
Пусть дана цепочка функций y=f(z), Dz, z=(x), Ez, Dx. Если область значений Dx является частью определения первой функции, тогда можно определить понятие функция от функции y=f[(x)]

Наложение или суперпозиция 2 функций f и .

Обратная функция — функция, обращающая зависимость, выражаемую данной функцией.

Функция является обратной к функции , если выполнены следующие тождества:

• f(g(y)) = y для всех

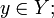
• g(f(x)) = x для всех

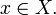
4.Определение предела функции на языке (в точке, на плюс минус беск, конечный, равный беск.) Правосторонний и левосторонний пределы.

Определение 1 . xa -> yb . Число b называется пределом функции f(x) при , если для любого как угодно малого положительного числа эпсилон найдется такое положительное число дельта, что как только аргумент отстоит от своего предела а, на расстояние меньше, чем дельта, так сразу же функция будет отстоять от своего числа b на расстояние меньше, чем эпсилон.

Этот предел, который определяется в – называется двусторонним пределом функции при ха. Все равно с какой стороны х приближается к точки а, главное чтобы модуль разницы был меньше дельта х.

Определение 2. Левосторонний предел при х а, х<a.

Число b называется пределом f(x) при x стремящимся к а слева, если для любого как угодно малого числа эпсилон найдется как угодно малое дельта эпсилон, что как только так сразу будет выполняться

Определение 3. Правосторонний предел функций.

Число b называется пределом f(x) при x стремящимся к а справа, если для любого как угодно малого числа эпсилон найдется как угодно малое дельта эпсилон, что как только

так сразу же будет выполняться .

Если правосторонний предел при ха существует, то пишут

Существует тесная связь между односторонними пределами и двусторонним пределом функции и выражается в теореме.

Теорема. Двусторонний предел функции f(x) при ха существует тогда и только тогда, когда существуют оба односторонних предела и они равны друг другу. Т.е . будет выполняться соотношение

5.Бесконечно малая функция. Свойство бесконечно малых функций. Связь предела функции с бесконечно малой функцией.

Функция у=f(х) называется бесконечно малой при х→x_0,если

По определению предела функции равенство означает: для любого числа ε>0 найдется число δ>0 такое, что для всех х, удовлетворяющих неравенству 0<|х-x₀|<δ, выполняется неравенство |ƒ(х)|<ε.

Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми; обозначают обычно греческими буквами α, ß и т. д.

1 свойство предела функции. Если функция f(x) при x -> а имеет пределом число b тогда разность f(x)-b будет бесконечно малой величиной.

2 свойство. Если функция f(x) имеет предел b при x -> а, то этот предел единственный.

3 свойство. Критерий существования предела функции. Теорема о сжатой переменной.

Теорема. Если имеются три функции U(x), V(x), f(x), определенные на одном промежутке (А;B) и внутри промежутка имеется какое-то а, причем все они определены на этом промежутке

D_U=D_V=D_X=(A;B) и при этом для любого х из этого промежутка выполняется соотношение .

Переменная f(x) зажата между переменными U(x) и V(X). Существуют пределы крайних функций и эти пределы равны друг другу, тогда обязательно будет иметь предел и функция f(x) при x -> а и этот предел будет обязательно равен тому же числу b.

6.Бесконечно большая функция. Связь между бесконечно большой и бесконечно малой функцией.

Величина f(x) называется бесконечно большой если при , .

Для любого как угодно большого числа n найдется такое положительное дельта, что как только отличие аргумента х от числа а по модулю , так сразу же будет выполняться .

Для любого как угодно большого положительного числа М найдется положительное число ,что как только разность аргумента и а будет отстоять меньше чем на так сразу же f(x) будет меньше чем -М.

Теорема. Если f(x) является бесконечно большой при х а, то обратная величина ℒ будет бесконечно малой величиной при х а.

Верно и обратное утверждение если (x) является бесконечно малой величиной при х а, то обратная величина () будет бесконечно большой.

1 свойство. Если ℒ (х)и β(х) есть бесконечно малые при х а, то их сумма будет так же бесконечно малой при х а

Если ℒ (х)и β(х)есть бесконечно малые при х а, то и произведение этих двух величин будет стремиться к 0 при х а.

Следствие. Если ℒ (х)есть бесконечно малая величина при х а, а k есть константа, то тогда и произведение k на ℒ будет так же бесконечно малым.

7.Свойства пределов функции, связанные с арифметическими операциями над функциями.

8.Предельный переход в неравенствах.

Теорема 11. Если  и, начиная с некоторого номера, выполняется   , то   .

Доказательство. Пусть с некоторого номера выполняется . Предположим, что . Так как , то для  существует такой номер N, что для всех  выполняется  или , откуда получаем , что противоречит условию. Случай  рассматривается аналогично.

Следствие 1. Пусть  и  сходятся и, начиная с некоторого номера, выполняется , тогда .

Следствие 2. Пусть  сходится и при любом   , тогда и .

Доказательство. Так как , то и .

Теорема 12. Пусть  и с некоторого номера n выполняется условие . Тогда последовательность  сходится и .

9.Первый замечательный предел.

Теорема: Предел частного (отношения) двух бесконечно малых величин не изменяется, если одну из них (или обе) заменить эквивалентной величиной.

10.Непрерывность функции в точке и на промежутке. Свойство непрерывных функций. Непрерывность функции в точке справа и слева.

A B

Понятие непрерывности для последовательности не имеет смысла. Только для функции непрерывного аргумента.

Функция называется непрерывной в некоторой точке х₀ , принадлежащей области определения х₀ , если в этой точке выполняется следующее соотношение и этот предел равен значению функции в точке х₀.

Расширено определение для конечных точек промежутка Dx=[A;B] , если он замкнут.

Функция называется непрерывной на ловом конце промежутка А, если выполняется следующее соотношение

Функция называется непрерывной на правом конце промежутка области определения, если выполняется следующее соотношение

Кроме непрерывности функции в точке (определение 1) на практике важное значение имеет другая форма этого определения.

- приращение аргумента.

Функция называется непрерывной в точке , если в этой точке бесконечно малому приращению аргумента отвечает бесконечно малое приращение функции, то есть выполняется соотношение .

Если функция непрерывна в каждой точке замкнутого промежутка Dx=[A;B], то в этом случае говорят что функция непрерывна в этом промежутке.

Элементарные функции непрерывны во всех тех точках, где они определены, то есть непрерывны во всей области своего определения.

11.Точки разрыва функции, их классификация.

Важное значение при построении графика функции имеют точки, где условия непрерывности функции в точке, которые формулируются в определении, не выполняются.

Такие точки называются точками разрыва функции.

Выделяют 3 различных рода точек разрыва.

1)Разрыв 1 рода.

2)Как частный случай 1 - устранимый разрыв.

3)Разрыв 2 рода.

Разрыв 1 рода:

; ;

В этом случае оба односторонних предела существуют, но не равны друг другу.

– величина скачка функции в точке разрыва.

Пример:

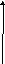
12.Теорема Вейерштрасса (без док).

Первая теорема Вейерштрасса: Если функция непрерывна на некотором промежутке, то она ограничена на нем.

Вторая теорема Вейерштрасса. Пусть функция определена и непрерывна в промежутке Dx=[A;B] , тогда в этом промежутке найдутся 2 такие точки (),в которых функция принимает свое наибольшее и наименьшее значение на этом промежутке.

13.Второй замечательный предел и его следствия.

14.Производная функции. Геометрический смысл производной. Правосторонняя и левосторонняя производные. Необходимые условия существования производной функции в точке.

предел отношения приращения функции к вызвавшему его приращению аргумента при стремлении последнего к нулю называется производной данной функции, вычисленной в данной точке.

Рассмотрим функцию

D_f=(A;B)

х₀

Возьмем точку х₀ принадлежащую этому промежутку. Придадим аргументу значению функции в этой точке . Придадим аргументу приращение . Перейдем в точку и этому будет соответствовать новое значение функции .

Разность между новым значением функции и прежним её значением принято обозначать или и она называется приращением функции, которая порождается приращением аргумента .

средняя скорость, с которой точка двигалась за время .

Чтобы вычислить мгновенную скорость в настоящее время надо уменьшать промежуток времени.

Предел 1:

Причем предполагается что функция непрерывна, поэтому при дельта , отношение будет стремится к , поэтому в числителе разность тоже будет стремится к нулю.

При вычислении предела 1 переменной величиной является , приращение аргумента функции. А точка – это константа.

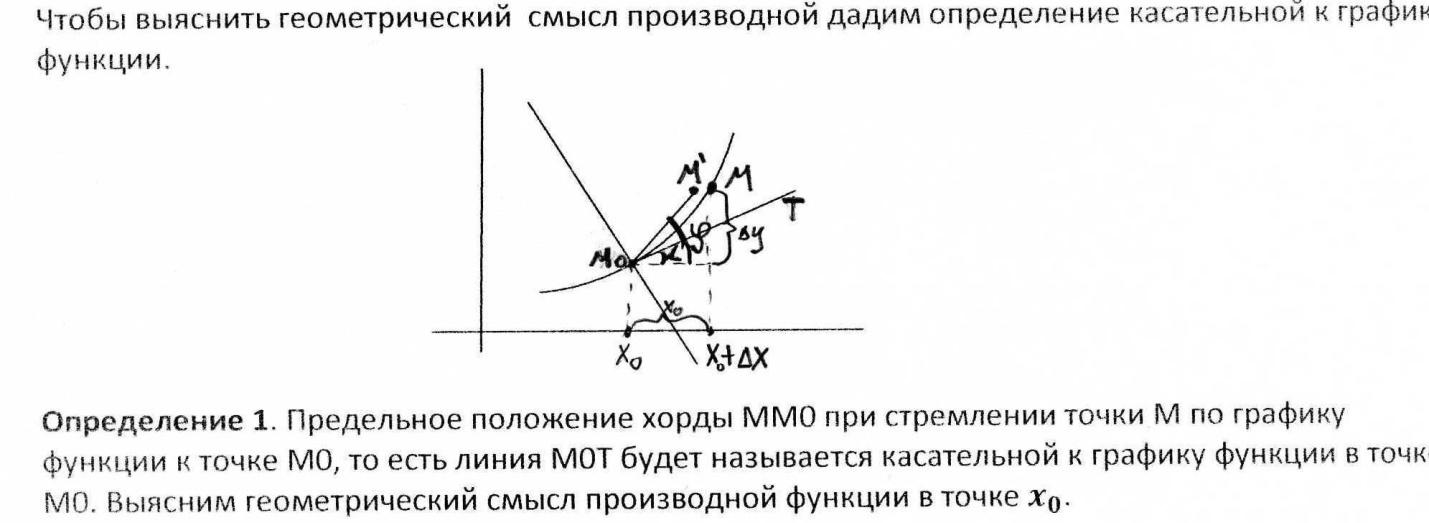
Из чертежа видно, что для хорды ММ0 тангенс угла наклона хорды к оси ох () ;

При стремлении М к М0 хорда будет приближаться к касательной, будет стремиться к нулю

(), поэтому предельное значение угла -

Оно и дает геометрический смысл.

Производная функции, вычисленная при с геометрической точки зрения представляет из себя угловой коэффициент касательной, проведенный к графику функций с соответствующими координатами (; ).

Уравнение касательной можно записать в следующем виде

Уравнение нормали:

(перпендикуляр касательной проведенной к точке )

Пусть функция у = f(x) определена в односторонней окрестности точки х = а, включая и саму эту точку. Если существуют конечные пределы или , то они называются соответственно левосторонней и правосторонней производной функции у = f(x) в точке х = а. Обозначение: .

15.Правила вычисления производных.

16.Таблица производных

Таблица производных основных элементарных функций :

17.Производная сложной функции (без док).

Правило дифференцирования сложной функции:

Пусть имеется функция сложная, присутствует функция от функции

Введем внутреннюю функцию промежуточный аргумент

Они эквивалентны.

Тогда теорема состоит в следующем -

Доказательство для монотонной функции.

18.Производные высших порядков.

Предел отношения приращения новой функции вызвавшему его приращение аргумента при стремлении последнего к нулю. Если этот предел существует, то его обозначают через y``.

По отношению к исходной функции имеет смысл производной от первой производной. Это производная второго порядка исходной функции. Тем самым дано определение производной второго порядка от функции .

Правило вычисления производных второго порядка обычно совпадает с правилами вычисления первого порядка. Только функцию заменяют на функцию .

Вычислять производную второго порядка можно только когда известна производная первого порядка.

Правило вычисления производной второго порядка -

Из формулы вытекает, что вторую производную можно представить как отношение дифференциала к квадрату дифференциалу независимого аргумента.

Аналогично может быть определены производные третьего порядка исходной функции.