1)Линейное векторное н-мерное пространство

Определение 1. Упорядоченная совокупность из n действительных чисел (а₁, а₂, …, а_n) называется n-мерным вектором ā(а₁, а₂, …, а_n). Числа а₁, а₂, ..., а_n называются координатами вектора.

Два n-мерных вектора (а₁, а₂, …, а_n) и (b₁, b₂, …, b_n) считаются равными, если равны их соответствующие координаты:

, ().

Вектор, все координаты которого равны нулю, называется ноль-вектором и обозначается .

Определение 2. Суммой (разностью) двух n-мерных векторов (а₁, а₂, …, а_n) и (b₁, b₂, …, b_n) называется n-мерный вектор, координаты которого равны суммам (разностям) соответствующих координат исходных векторов:

=(a₁b₁; a₂b₂; …; a_nb_n).

Определение 3. Произведением n-мерного вектора (а₁, а₂, …, а_n) на число k называется n‑мерный вектор, координаты которого равны произведениям координат вектора на числоk:

k · =(ka₁; ka₂; …; ka_n).

Для геометрических векторов (n<4) эти операции эквивалентны правилу параллелограмма или треугольника и растяжению (сжатию) вектора.

Свойства операций над векторами:

1) +=+- коммутативность,

2) +(+)=(+)+- ассоциативность,

3) k·()=k·k·                   - дистрибутивность,

4) (k₁k₂)·= k_{1 ·} k₂·,

5) (k₁·k₂)·=k₁·(k₂·),

6) 1·=,

7) 0·=,

8) k·=,

9) k·=.

Определение 4. Совокупность всех n-мерных векторов с введенными на ней операциями сложения и умножения на число называется n-мерным линейным векторным пространством и обозначается Eⁿ.

2) Скалярное произведение. Угол между векторами.

Определение 1. Скалярным произведением двух n-мерных векторов (а₁, а₂, ..., а_n) и (b₁, b₂, ..., b_n) называется число, равное сумме попарных произведений соответствующих координат.

·=а₁·b₁+a₂·b₂+…+a_n·b_n.

Свойства скалярного произведения:

1. ·=·- коммутативность;

2. ·(+)=·+·- дистрибутивность;

3. k·(·)=(k·)·,

4. ·=², ²=0.

Определение 2. Длиной n-мерного вектора называется величина:

.

Определение 3. Углом между двумя ненулевыми n-мерными векторами называется угол, косинус которого вычисляется по формуле

.

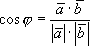3) Условие коллинеарности и ортогональности векторов.

Определение 1. Два n-мерных вектора  и называются коллинеарными, если найдется числотакое, что=·.

Рассмотрим два коллинеарных вектора и. Так как они коллинеарны, то=·, или (a_1, a_2, …, a_n)=( b_1, b_2, …,  b_n ). Следовательно, a₁= b_1, a₂= _2, …, a_n= b_n.

Выражая из этих равенств , получим

 - условие коллинеарности.

Для того чтобы два вектора были коллинеарными, необходимо и достаточно, чтобы их координаты были пропорциональны.

Найдем угол между коллинеарными векторами.

.

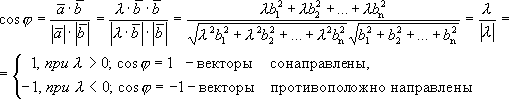Определение 2. Два ненулевых n-мерных вектора иназываются ортогональными, или перпендикулярными, если угол между ними равен 90°.

,

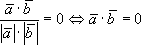 - условие ортогональности.

4) Системы векторов.

Пусть дана система n-мерных векторов .

Определение 1. Линейной комбинацией системы векторов называется выражение вида

,

где с₁, с₂, …, с_k - некоторые числа.

Определение 2. Выпуклой линейной комбинацией системы векторов называют линейную комбинацию, в которой все коэффициенты неотрицательны и сумма всех коэффициентов равна единице.

; ,;.

Определение 3. Вектор разлагается по системе векторов, если его можно представить в виде линейной комбинации векторов этой системы.

.

5) Ранг и базис системы векторов и всего пространства.

  Определение 1. Рангом системы векторов называется максимальное число линейно независимых векторов системы.

.

            Определение 2. Базисом системы векторов называется максимальная линейно независимая подсистема данной системы векторов.

            Теорема. Любой вектор системы можно представить в виде линейной комбинации векторов базиса системы. (Всякий вектор системы можно разложить по векторам базиса.) Коэффициенты разложения определяются для данного вектора и данного базиса однозначно.

            Доказательство. Пусть система  имеет базис .

            1 случай. Вектор  - из базиса. Следовательно, он равен одному из векторов базиса, допустим . Тогда =.

            2 случай. Вектор  - не из базиса. Тогда r>k.

Рассмотрим систему векторов . Данная система является линейно зависимой, так как  - базис, т.е. максимальная линейно независимая подсистема. Следовательно, найдутся числа с₁, с₂, …, с_k, с, не все равные нулю, такие, что

= .

Очевидно, что  (если с=0, то базис системы является линейно зависимым).

.

Докажем, что разложение вектора по базису единственно. Предположим противное: имеется два разложения вектора по базису.

=,

=.

Вычитая эти равенства, получим

.

Учитывая линейную независимость векторов базиса, получим

.

Следовательно, разложение вектора по базису единственно.

Количество векторов в любом базисе системы одинаково и равно рангу системы векторов.

         

Ранг и базис n‑мерного линейного

векторного пространства

 

            Теорема 1. Ранг n-мерного пространства равен его размерности: r=n.

            Доказательство. На основании теоремы Штейница ранг не превышает n. С другой стороны, в пространстве имеется система из n линейно независимых единичных векторов, следовательно, ранг не меньше n. Значит, базис содержит nвекторов.

            Следствие 1. Любой базис n-мерного пространства состоит из n линейно независимых n-мерных векторов.

            Следствие 2. Любая система в n-мерном пространстве, содержащая больше чем n векторов, линейно зависима.

            Следствие 3. Любой вектор пространства можно однозначно разложить по векторам любого базиса. Коэффициенты разложения для данного вектора и данного базиса определяются единственным образом. Коэффициенты разложения называются координатами данного вектора в этом базисе.