1 Поступательное движение Вращательное движение

Скорость  Угловая скорость  Ускорение Угловое ускорение 

2 Адиабатическим называется процесс, при котором отсутствует теплообмен (δQ=0) между системой и окружающей средой. Адиабатическим процессами можно считать все быстропротекающие процессы. Таковым, например, можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько большая по значению, что обмен энергией между средой и волной произойти не успевает. Адиабатические процессы происходят в двигателях внутреннего сгорания (сжатие и расширение горючей смеси в цилиндрах), в холодильных установках и т. д.  Из первого начала термодинамики (δQ=dU+δA) для адиабатического процесса следует, что   (1)  т. е. внешняя работа совершается за счет изменения внутренней энергии системы.  Используя формулы δA=pdV и C_V=dU_m/dT, для произвольной массы газа перепишем уравнение (1) в виде   (2)  применив дифференцирование уравнение состояния для идеального газа pV=(m/M)RT получим   (3)  Исключим из (2) и (3) температуру Т.    Разделив переменные и учитывая, что С_p/С_V=γ , найдем    Проинтегрируя это уравнение в пределах от p₁ до p₂ и соответственно от V₁ до V₂, и потенцируя, придем к выражению   или  Так как состояния 1 и 2 выбраны произвольно, то можно записать   (4)  Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.  Для перехода к переменным Т, V или p, Т исключим из (55.4) с помощью уравнения Менделеева-Клапейрона    соответственно давление или объем:   (5)   (6)  Выражения (4) — (6) представляют собой уравнения адиабатического процесса. В них безразмерная величина   (7)  называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i=3, γ=1,67. Для двухатомных газов (Н₂, N₂, О₂ и др.) i=5, γ=1,4. Значения γ, вычисленные по формуле (55.7), хорошо подтверждаются экспериментом. 

Билет 22

1 Момент инерции. Момент инерции - это величина равная сумме произведений всех масс на квадраты их расстояний от некоторой оси,

I= m_ir_i².

 Моменты инерций простейших тел.

1. Материальная точка I=mr².

2. Тонкий однородный стержень I=1/12ml², при оси проходящей через его центр масс.

3. Обруч I=mr².

4. Диск I=1/2mr².

5. Шар I=2/5mr².

Момент инерции для сплошного цилиндра

dI=m_ir_i²=ρ*V_i* r_i²=ρ*2*π* r_i*h*dr*r²

dI=2*π*ρ*h* r_i³*dr

I=2*π*ρ*h{0-R}∫ r_i³dr

I=2*π*ρ*h*(R⁴/4)-(m*R²/2)

I=1/2*m*R²

Кинетическая энергия вращающения.

E_k=Σ(m_iw²R_i²)/2=w²/2*Σm_iR_i²

E_k=(I*w²)/2 – для вращательного движения тела

E_k=(I*w²)/2+(m*v²)/2 – для вращательного и поступательного движения.

 

Момент силы. Моментом силы F относительно некоторой точки O называется векторная величина M, M=r*F*Sin ,r-радиус-вектор l=r*sin , l-плечо силы. M=F*l;

Плечо силы – это кротчайшее расстояние от точки вращения до линии вдоль которой действует сила

Момент силы относительно оси это проекция момента силы относительно любой точки оси на данную ось.

2 Среди равновесных процессов, которые происходят с термодинамическими системами, отдельно рассматриваются изопроцессы, при которых один из основных параметров состояния остается постоянным.  Изохорный процесс (V=const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат (рис. 1), где процесс 1—2 есть изохорное нагревание, а 1—3 — изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.  Из первого начала термодинамики (δQ=dU+δA) для изохорного процесса следует, что вся теплота, которая сообщается газу, идет на увеличение его внутренней энергии:  т.к. C_V=dU_m/dt,  Тогда для произвольной массы газа получим  (1)  Изобарный процесс (p=const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, которая параллельна оси V. При изобарном процессе работа газа при увеличения объема от V₁ до V₂ равна  (2)  и равна площади заштрихованного прямоугольника (рис. 2). Если использовать уравнение Менделеева-Клапейрона для выбранных нами двух состояний, то  и откуда  Тогда выражение (2) для работы изобарного расширения примет вид  (3)  Из этого выражения вытекает физический смысл молярной газовой постоянной R: если T₂ —T₁ = 1К, то для 1 моль газа R=A, т. е. R численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1 К. 

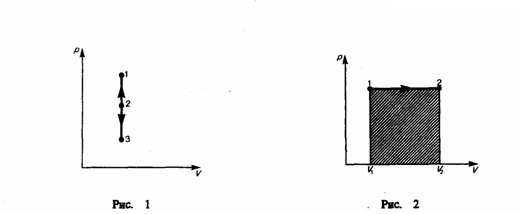
Рис.1

В изобарном процессе при сообщении газу массой m количества теплоты  его внутренняя энергия возрастает на величину (т.к. C_V=dU_m/dt)  При этом газ совершит работу, определяемую выражением (3).  Изотермический процесс (T=const). Изотермический процесс описывается законом Бойля—Мариотта:  Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу, которая расположена на диаграмме тем выше, чем выше температура, при которой происходит процесс.  Исходя из формул для работы газа и уравнения Менделеева-Клайперона найдем работу изотермического расширения газа:  Так как при Т=const внутренняя энергия идеального газа не изменяется:  то из первого начала термодинамики (δQ=dU+δA) следует, что для изотермического процесса  т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:  (4)  Значит, для того чтобы при расширении газа температура не становилась меньше, к газу в течение изотермического процесса необходимо подводить количество теплоты, равное внешней работе расширения. 

Билет 23