6.3. Алгоритмы выработки параметров ориентации в биим на позиционных гироскопах

Для выработки параметров ориентации в БИИМ на ПГ типа ЭСГ, как правило, вводят правый ортогональный трехгранник , орты которого, например, следующим образом построены на ортахвекторови(рис.6.9) (т.е. необходимо решениезадачи ортогонализации):

,,, (6.26)

где - угол между векторами, причем.

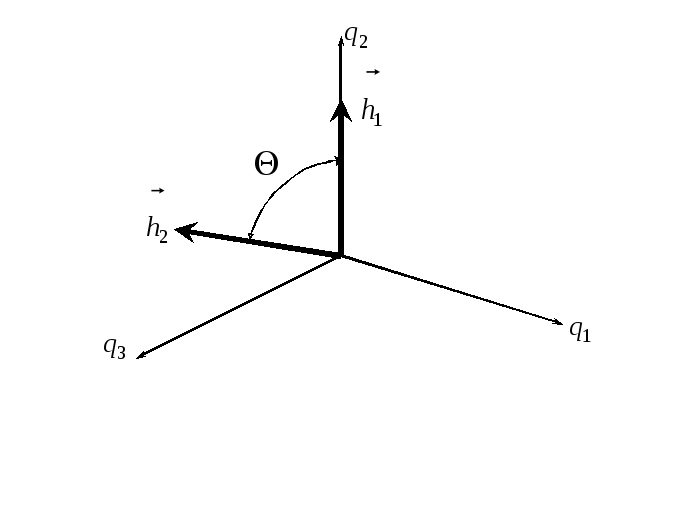
Рис.6.9. Система координат , связанная с ортамикинетических моментов ЭСГ

Ориентацию трехгранника относительно связанной с ИБ системы координатопределим в этом случае следующей матрицей направляющих косинусов

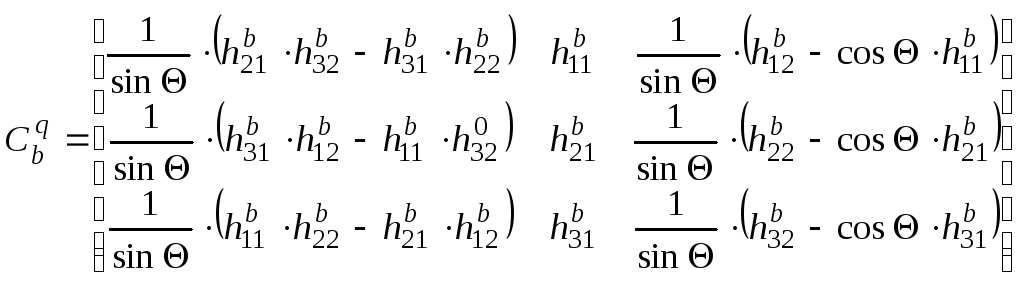. (6.27)

Элементы искомой матрицы направляющих косинусов, определяющей взаимную ориентацию связанной с ИБ системы координат и географического сопровождающего трехгранника, могут быть вычислены в соответствии с матричным соотношением:

. (6.28)

В БИИМ на ЭСГ исходными являются направляющие косинусы ортов векторов кинетических моментов ЭСГ относительно правых ортогональных систем координати(рис.6.10), связанных с корпусами гироскопов, соответственно:

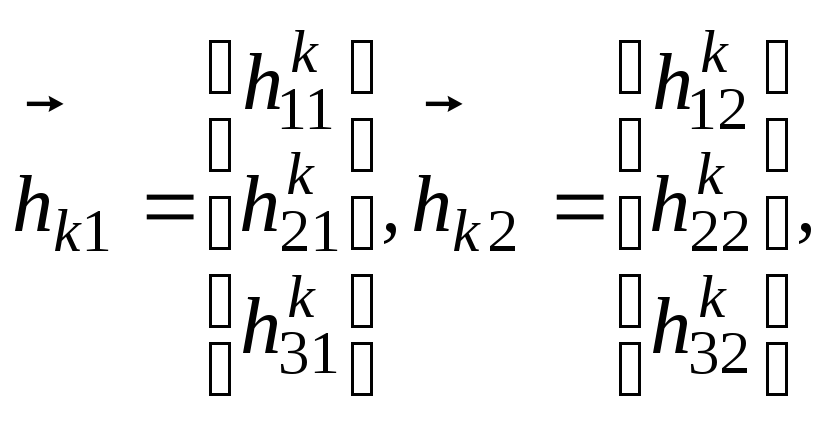(6.29)

Направляющие косинусы этих же ортов в связанной с ИБ системе координат могут быть найдены в соответствии с рис.6.10, как

, (6.30)

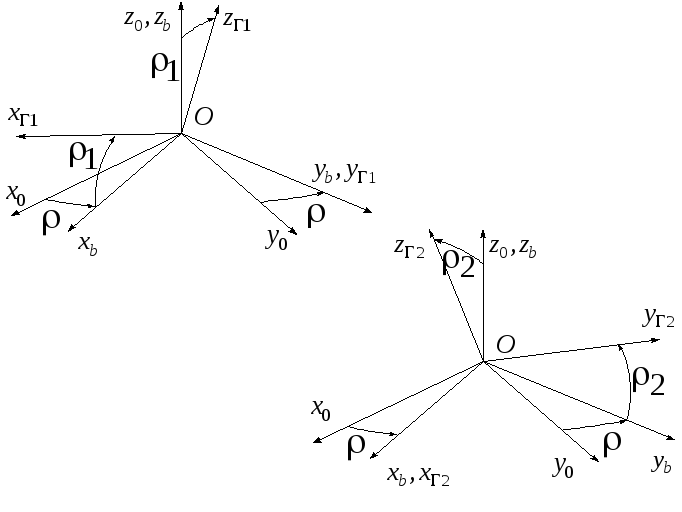
Рис.6.10. Ориентация систем координат и, связанных с корпусами ЭСГ, относительно корпуса объекта и блока ЧЭ

Для нахождения матрицы , учитывающей прецессию трехгранникав инерциальной системе координат, необходимо вычисление текущей ориентации ортоввекторовив ИСК, т.е. вычисление их направляющих косинусов в ИСК:

. (6.31)

Заметим, что эти направляющие косинусы рассчитываются в вычислителе БИИМ по известным паспортным (откалиброванным) значениям детерминированных составляющих дрейфов гироскопов в соответствии с принятой расчетной моделью уходов ЭСГ. Ориентация орта векторакинетического момента ЭСГ в инерциальной системе координат, помимо направляющих косинусов (6.31), может быть задана двумя углами Эйлера (рис.6.11): либо- прямым восхождением и склонением либо углами, заданными относительно системы координат, связанной с меридианом места. Через эти углы направляющие косинусы (6.31) определяются следующими соотношениями:

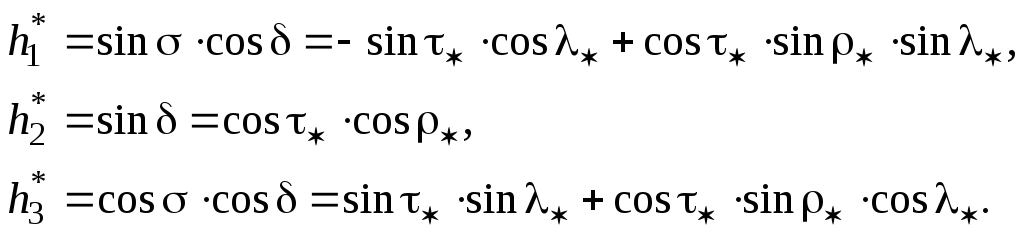(6.32)

Движение орта векторакинетического момента ЭСГ в инерциальной системе координат может быть описано векторным дифференциальным уравнением:

, (6.33)

где - вектор угловой скорости ухода (дрейф) гироскопа,- начальное положение орта вектора кинетического момента гироскопа в инерциальной системе координат.

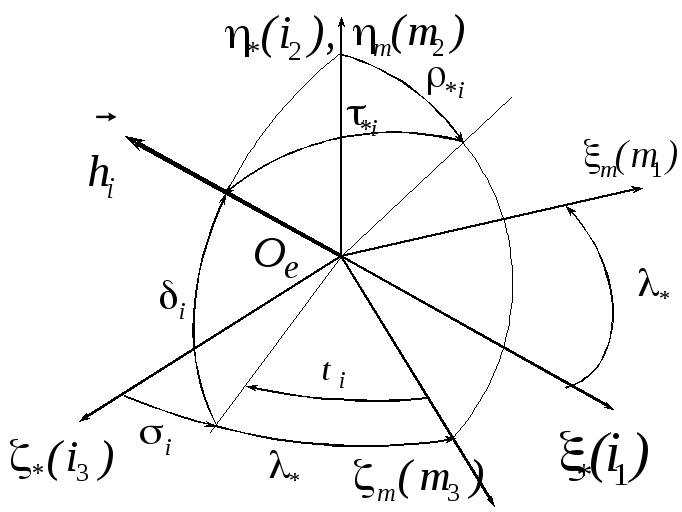
Рис.6.11. Ориентация орта векторакинетического момента ЭСГ в инерциальной системе координат

Скалярные дифференциальные уравнения для направляющих косинусов орта векторакинетического момента гироскопа в инерциальной системе координат будут:

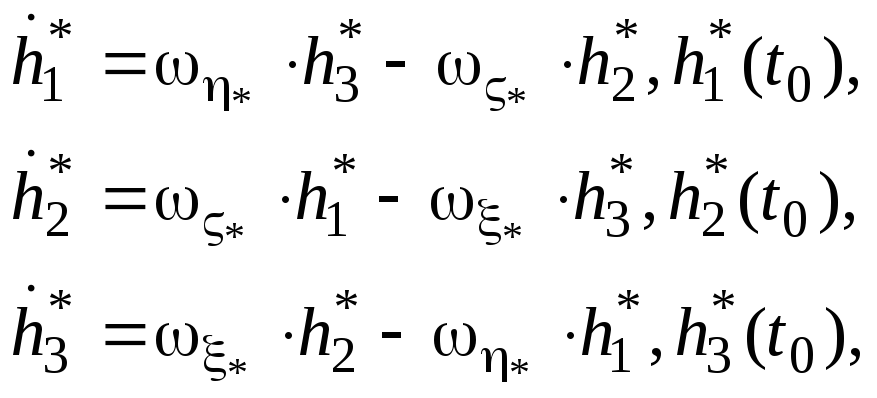(6.34)

где - соответствующие проекции вектора дрейфа гироскопа на оси инерциальной системы координат.

В соответствии с принятым условием (6.26) задачи ортогонализации находим, что

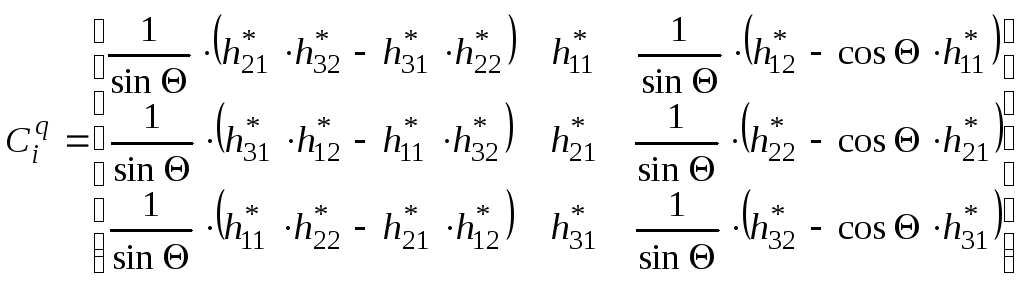. (6.35)

Дрейф гироскопа включает как детерминированные (систематические), так и случайные составляющие. Основные детерминированные составляющие дрейфа могут быть математически описаны в его модели. Модель дрейфа гироскопа используется для алгоритмической компенсации его систематических уходов в БИИМ. В настоящее время получена модель дрейфа ЭСГ для БИИМ, которая учитывает как консервативную природу пондеромоторных сил электростатического подвеса, так и неконсервантивные уводящие моменты, обусловленные магнитным взаимодействием корпуса и ротора[19, 24, 43, 82].

Отметим, что программное (расчетное) движение или положение трехгранника относительно инерциальной системы координат может быть осуществлено также интегрированием уравнения Пуассона:

, (6.36)

где - начальное значение матрицы;

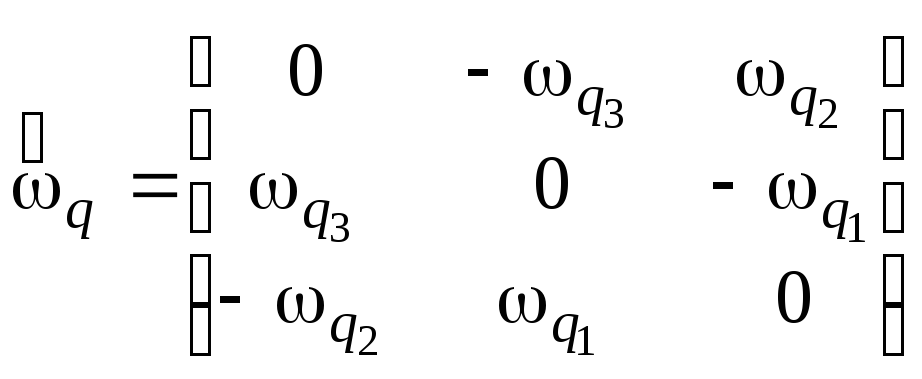- кососимметрическая матрица, элементы которой являются проекциями векторадрейфа трехгранникана его оси, который определяется векторным соотношением [2]:

(6.37)

где - векторы систематических дрейфов соответственно ЭСГ₁и ЭСГ₂.

Вектор систематического дрейфа трехгранникана его оси может быть определен также выражением:

(6.38)

Отметим, что для обеспечения ортогональности матриц (6.27) и (6.35), значение угла вычисляется по следующим формулам:

а) для соотношений (6.27)

; (6.39)

б) для соотношений (6.35)

. (6.40)

Для нахождения искомой матрицы направляющих косинусов согласно соотношению (6.28)

,

необходимо также знание матрицы направляющих косинусов, определяющей взаимную ориентацию горизонтной и инерциальной систем координат, которая в соответствии с (6.1) вычисляется по значениям выработанных в БИИМ координат места.

Искомые углы вычисляются из значений элементов матрицы

,

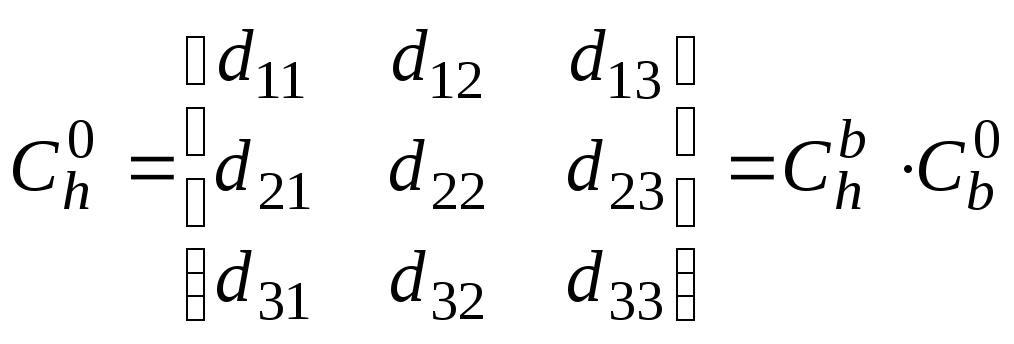(где - матрица направляющих косинусов, определяющая ориентацию связанной с ИБ системы координатотносительно связанной с корпусом объекта системы координат)

по формулам, определенным соотношениями (6.22)…(6.25).

Вычисление скоростей изменения углов курса и качек в БИИМ на ПГ требует численного дифференцирования параметров ориентации, что является особенностью таких систем.