6.2. Алгоритмы выработки параметров ориентации в биим на дус и иуу

Под решением задачи ориентации в БИИМ прежде всего понимается определение параметров ориентации ИБ БИИМ, т.е. нахождение матрицы ориентации трехгранникаотносительно сопровождающего географического трехгранника(которая используется в алгоритмах БИИМ для преобразования кажущихся ускорений, измеренных линейными акселерометрами, на навигационные оси для решения задачи навигации). И как следствие решения задачи ориентации ИБ БИИМ уже затем вычисляются параметры ориентации объекта, т.е. вычисляются значения матрицыи углов курса, килевой качкии бортовой качки, являющихся выходными данными БИИМ (рис.6.4).

Искомые матрицы ориентации могут быть определены как:

,

, (6.7)

где 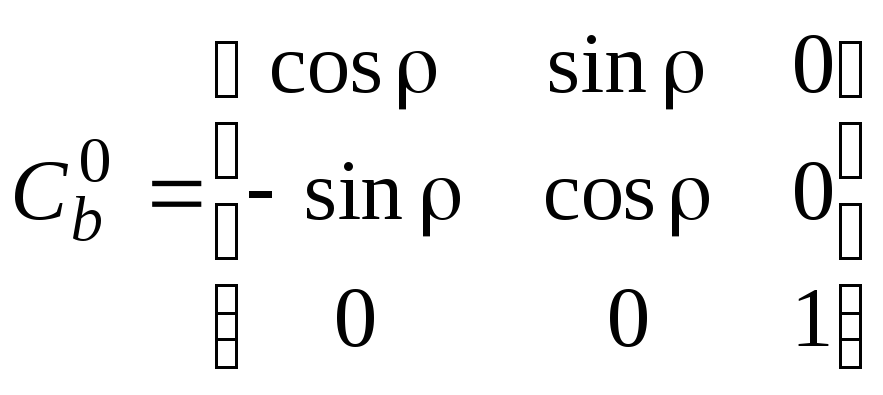- матрица направляющих косинусов, определяющая ориентацию связанной с ИБ системы координатотносительно осейобъекта (рис.6.8) и вычисляемая по данным соответствующего датчика угла (ДУ) об угле- при модуляционных поворотах ИБ;

- матрица начальной привязки осей ИБ к осям объекта – при неподвижном положении ИБ в осях объекта.

Если исходной информацией для вычисления параметров ориентации являются составляющие вектора угловой скорости вращения связанной с измерительным блоком системы координатна ее оси (БИИМ на ДУС), т.е.

, (6.8)

то элементы матрицы могут быть вычислены интегрированием кинематического уравнения или, как его иногда называют,уравнения Пуассона[1]:

(6.9)

где 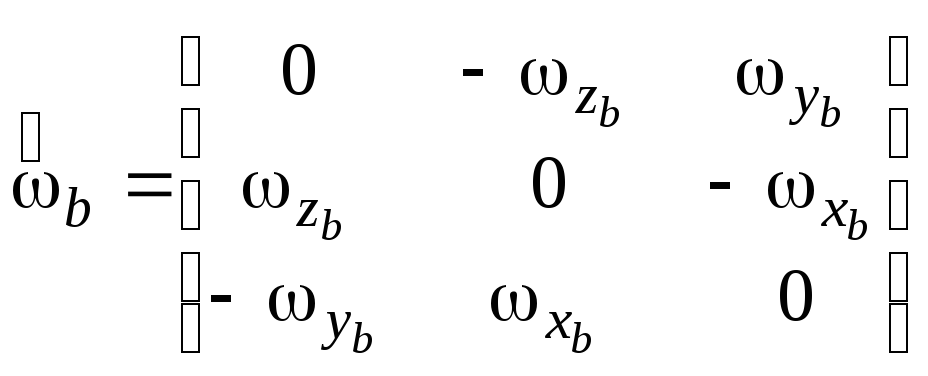- кососимметрическая матрица, соответствующая векторуугловой скорости вращения трехгранника;

- начальное значение матрицы.

Рис.6.8. Ориентация связанной с ИБ системы координат относительно связанной с корпусом объекта системы координат

Заметим, что для безгироскопных БИИМ на ИУУ составляющие вектора могут быть вычислены:

• в случае УА - интегрированием составляющих 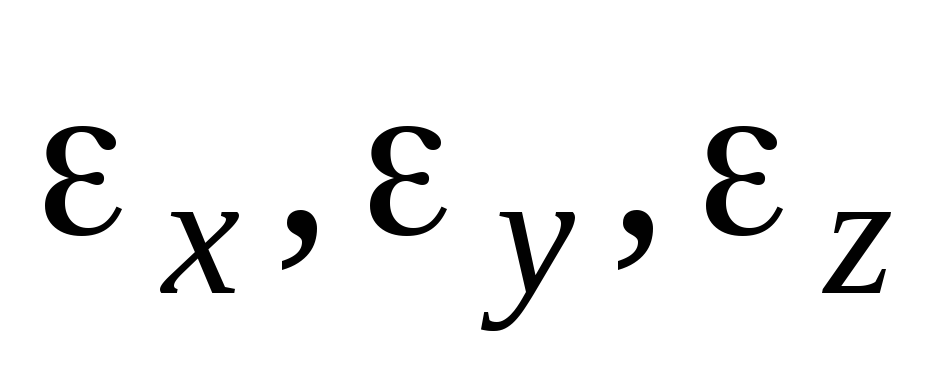векторауглового ускорения трехгранника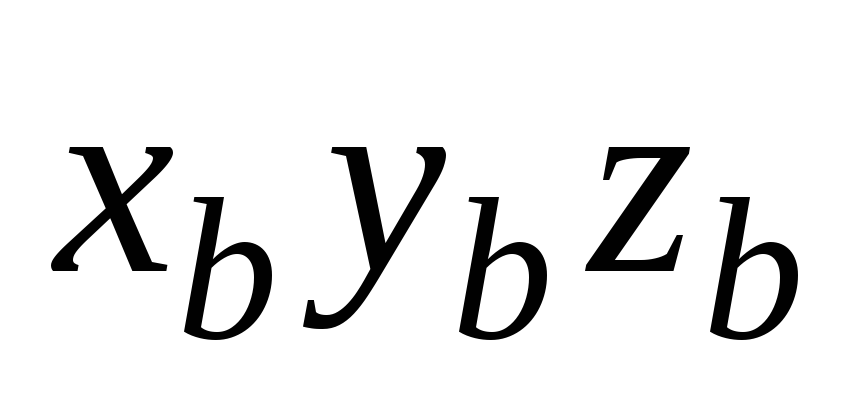на свои оси

(6.10)

где - значение соответствующих составляющих угловых скоростей в начальный момент времени.

• в случае разнесенных линейных акселерометров - интегрированием разностей кажущихся ускорений:

(6.11)

где - расстояния, характеризующие пространственное разнесение соответствующих линейных акселерометров.

Элементы матрицы , входящей в (6.7), должны вычисляться в соответствии с (6.1) по значениям выработанных в БИИМ координат места.

Матрица ориентации , определяющая ориентацию связанного с ИБ трехгранникаотносительно навигационных осей, может быть определена также непосредственно интегрированием уравнения Пуассона в виде [1]:

(6.12)

где 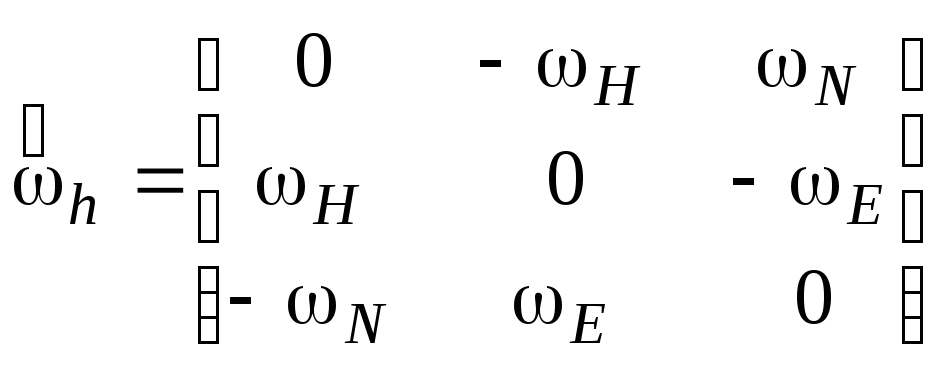- кососимметрическая матрица, соответствующая векторуугловой скорости вращения географического сопровождающего трехгранника;- начальное значение матрицы.

Составляющие вектора угловой скорости вращения географического сопровождающего трехгранника определяются соотношениями:

,,

, (6.13)

где град./ч - угловая скорость суточного вращения Земли;

(6.14)

и для эллипсоида Красовского м.

Кинематические уравнения, связывающие вектор угловой скорости и параметры ориентации в виде углов Эйлера-Крылова, имеют вид:

;

Для уменьшения требуемой производительности и объема памяти БЦВМ, а также снижения вычислительных погрешностей при решении задачи ориентации в современных БИИМ на ДУС вначале осуществляется вычисление элементов вектора Эйлера в качестве промежуточного кинематического параметра. А затем по известным соотношениям осуществляется вычисление параметров Родрига-Гамильтона (элементов соответствующего кватерниона) и элементов матриц ,направляющих косинусов [16, 39, 49].

Кинематические уравнения, связывающие вектор угловой скорости и вектор Эйлера

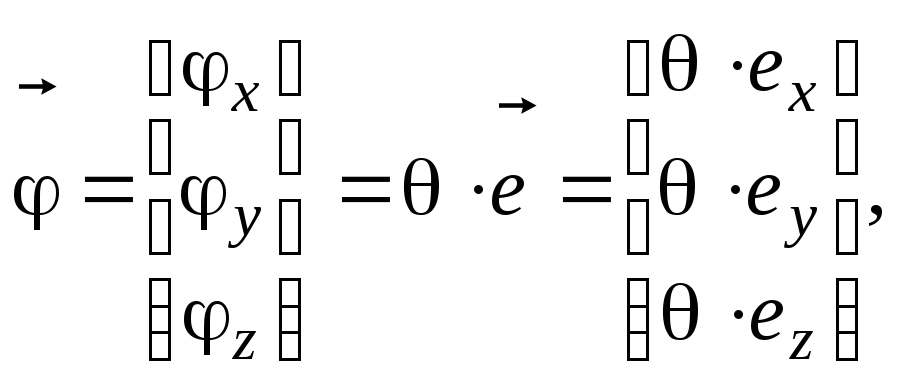
где ,- направляющие косинусы ортав подвижном базисе(),

имеют вид:

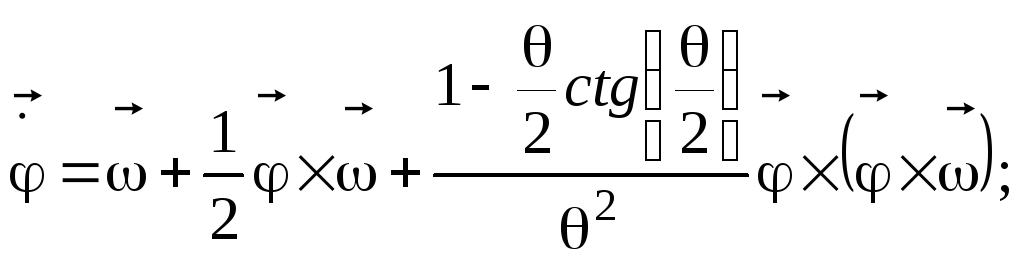(6.15)

Интегрируя уравнение (6.15), вычисляются составляющие вектора Эйлера. После чего, в соответствии с соотношениями

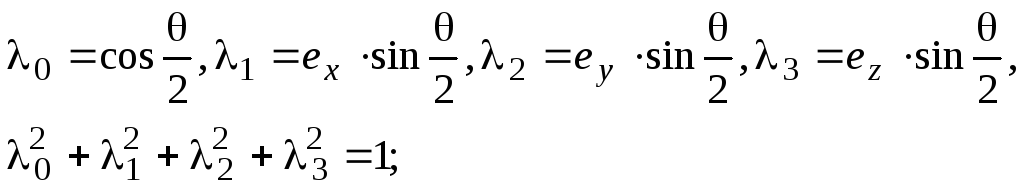(6.16)

,

могут быть сформированы элементы кватерниона .

Искомый кватернион , определяющий ориентацию измерительного блокаотносительно горизонтной системы координатс географической ориентацией осей, может быть найден по теореме сложения преобразований или в виде “кватернионного” произведения:

(6.17)

где верхние и нижние индексы кватернионов соответствуют системам координат относительно которых они определяют ориентацию, обозначает сопряженный кватернион, а знак () - оператор “умножения” кватернионов.

Компоненты кватерниона могут быть вычислены либо через составляющие вектора Эйлера либо непосредственно интегрированием уравнения Пуассона:

(6.18)

или в векторно-матричной форме (здесь и далее опуская у компонентов кватерниона верхние и нижние индексы)

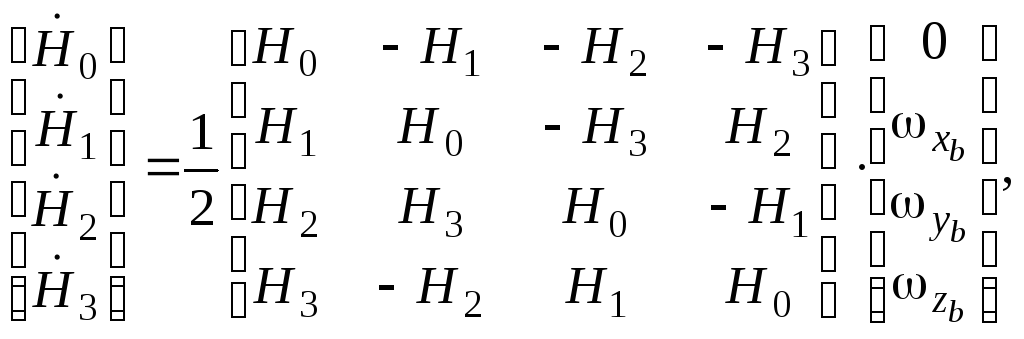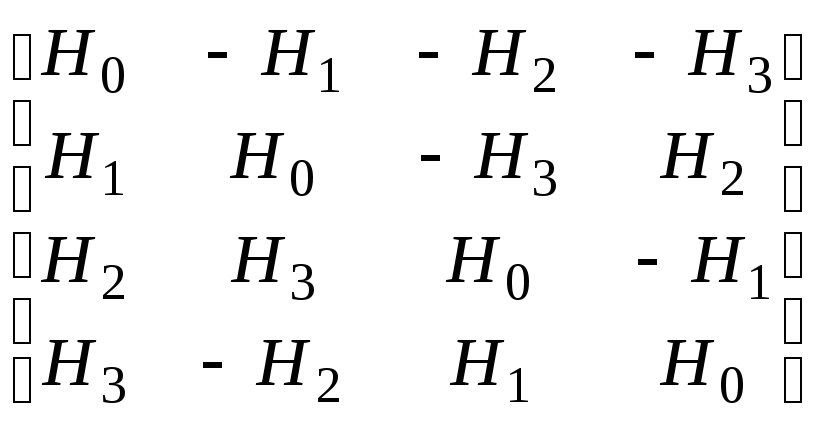где- матрица, соответствующая кватернионному произведению;

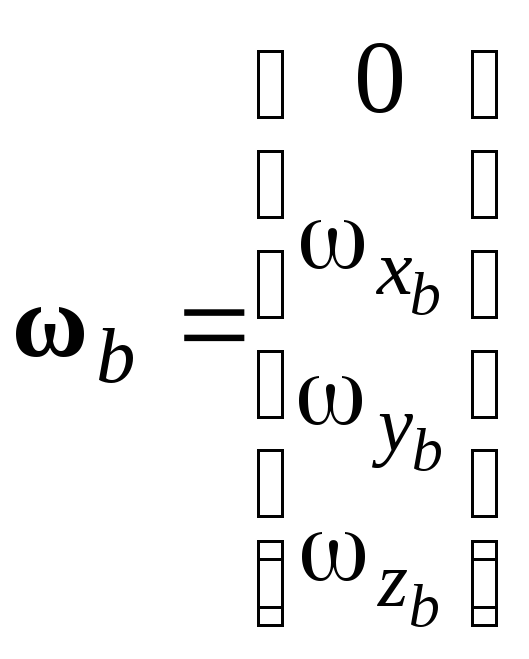- кватернион, соответствующий вектору.

Элементы кватерниона вычисляются аналогично

(6.19)

где 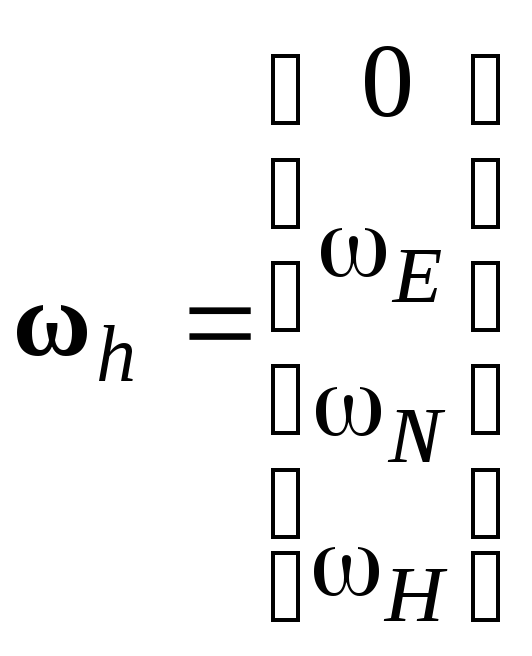- кватернион, соответствующий вектору.

Матрица ортогонального преобразования или матрица направляющих косинусов, определяющая взаимную ориентацию подвижной и неподвижной систем координат, выражается через элементы кватернионаследующим образом:

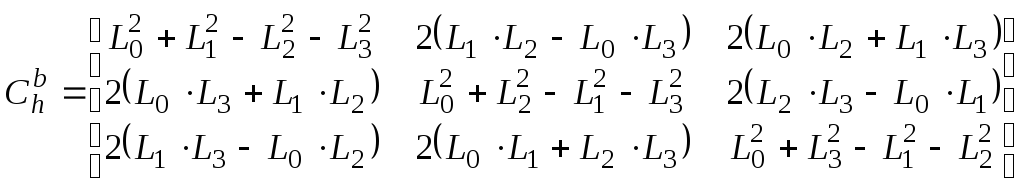. (6.20)

Для получения выходных параметров ориентации, т.е. углов необходимо знание элементов матрицы:

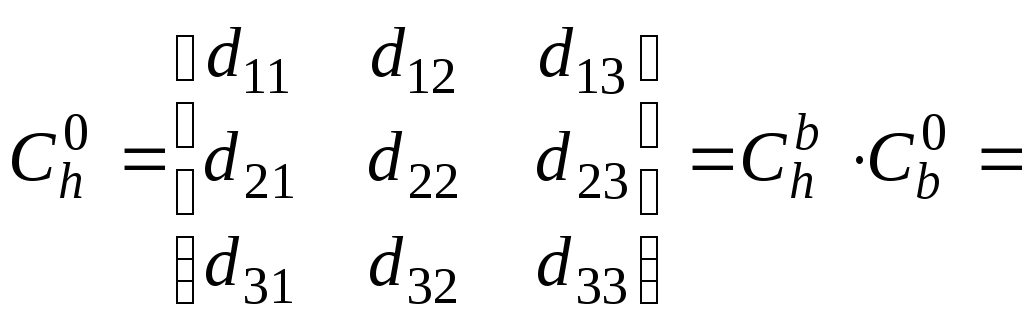
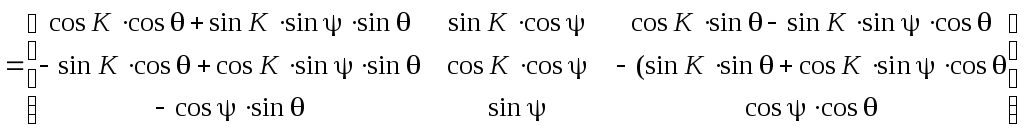, (6.21)

где 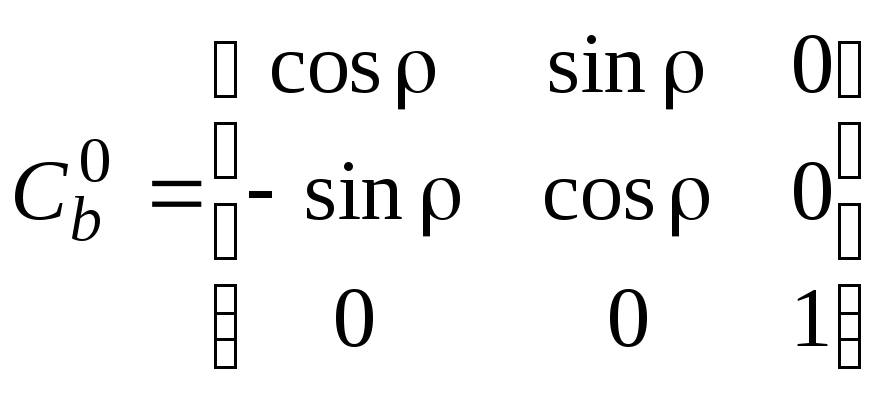- матрица направляющих косинусов, определяющая ориентацию связанной с ИБ системы координатотносительно связанной с корпусом объекта системы координат.

Из элемента находим выражение для угла килевой качки:

(6.22)

Элементы ипозволяют определить угол бортовой качки:

. (6.23)

Поскольку модули углов именьше, то приведенные выше выражения однозначно определяют значения углов килевой и бортовой качек.

Для нахождения соотношения, однозначно определяющего курс , воспользуемся элементами матрици функциейMatlabatan2:

K=atan2(d12/d22); (6.24)

при

atan2<0

K=atan2(d12/d22)+2*pi; (6.25)