17

Л.7. Особенности дискретных алгоритмов бинс (биим)

Содержание

7.1. Задача ориентации - определение матрицы направляющих косинусов

• алгоритмы вычисления кватерниона

• дискретный алгоритм решения задачи ориентации

• о вычислительных дрейфах в БИИМ на ДУС

7.2. Задача интегрирования кажущегося ускорения объекта в навигационном базисе

7.3. Задача преобразования информации акселерометров в навигационный базис

• традиционные алгоритмы

• «инвариантные» алгоритмы

Приложение. Рекуррентные алгоритмы рассматриваемых задач

Приведенные выше непрерывные алгоритмы БИИМ являются замкнутыми, т.е. для вычисления соответствующих интегралов и преобразования переменных из одной системы координат в другую требуются непрерывные значения как самих переменных, так и их интегралов и элементов матриц преобразования, и поэтому не могут быть непосредственно реализованы в бортовом вычислителе системы, осуществляющем дискретную обработку информации. Кроме того, такие алгоритмы не учитывают реальный вид выходных сигналов современных датчиков первичной информации (линейных акселерометров, датчиков угловой скорости), которые, как правило, дискретно вырабатывают интегралы по времени от измеряемых параметров на такте опроса. Дискретная обработка информации в БЦВМ приводит к неизбежной аппроксимации непрерывных процессов дискретными, т.е. к квантованию непрерывных сигналов или к замене непрерывного во времени сигнала последовательностью чисел, представляющих значение этого же сигнала в определенные моменты времени.

7.1. Задача ориентации - определение матрицы направляющих косинусов

Рассмотрим дискретные алгоритмы, реализуемые в блоке выработки параметров ориентации, если исходными данными являются измерения проекций вектора угловой скорости вращения измерительного блока на его оси , а точнее угловых квазикоординат (проекций приращений угла поворота ИБ на связанные оси).

В современных БИИМ для уменьшения требуемого объема памяти и требуемой производительности бортовых вычислителей задача ориентация ИБ часто сводится к вычислению кватерниона - четырехкомпонентного вектора. Элементами кватерниона являются параметры Родрига-Гамильтона . При этом в качестве промежуточного кинематического параметра, как правило, осуществляется вычисление составляющих вектора Эйлера.

Алгоритмы вычисления кватерниона

Искомый кватернион , определяющий ориентацию измерительного блока относительно географического сопровождающего трехгранника , может быть найден по теореме сложения преобразований или в виде “кватернионного” произведения:

(7.1)

где верхние и нижние индексы кватернионов соответствуют системам координат относительно которых они определяют ориентацию, обозначает сопряженный кватернион, а знак () - оператор “умножения” кватернионов.

Компоненты кватерниона могут быть вычислены интегрированием кинематического уравнения:

. (7.2)

Элементы кватерниона вычисляются как

(7.3)

или по значениям выработанных в БИИМ координат места в соответствии со следующими соотношениями

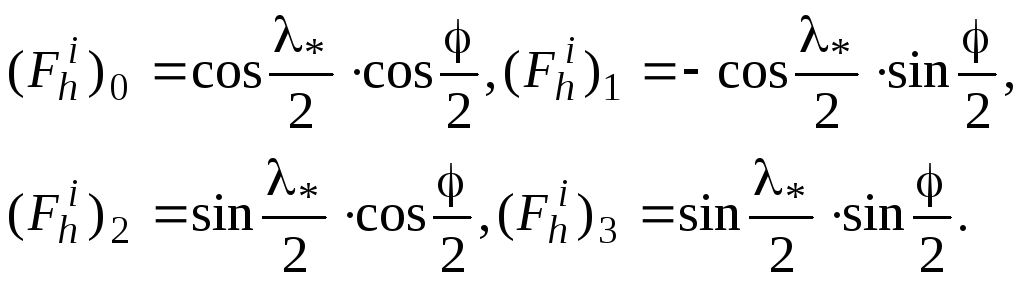(7.3а)

Для вычисления кватернионов , используются дискретные алгоритмы, представляющие собой приближенные решения уравнений (7.2), (7.3) на шаге интегрирования.

Однако наиболее развиты и исследованы дискретные алгоритмы интегрирования кинематического уравнения вращательного движения объекта для составляющих вектора Эйлера.

Приведем дискретный алгоритм решения задачи ориентации

(учитывая при этом, что в качестве промежуточного кинематического параметра осуществляется вычисление на шаге интегрирования составляющих вектора Эйлера)

Согласно соотношениям

, или

,

где - приращение кватернионов на шаге dT,

для дискретного алгоритма имеем

; (7.4)

%Формирование вектора Эйлера (вектора ориентации) по .

В общем случае, когда на такте вычислений вектор изменяет свою величину и направление в инерциальном пространстве, производная вектора ориентации связана с вектором угловой скорости вращения связанной с измерительным блоком системы координат соотношением:

. (7.5)

где - модуль вектора (значение угла поворота).

Разложением коэффициента при третьем слагаемом (7.5) в степенной ряд до первого порядка относительно величины можно показать, что

т. е. вектор на такте вычислений может быть определен как

В настоящее время, как правило, пренебрегают третьим членом в уравнении (7.5), а под интегралом выражают через интеграл от

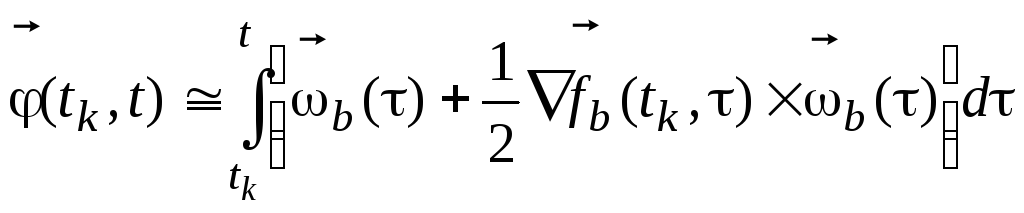, (7.6)

где , ( - такт опроса гироскопов).

Дискретные алгоритмы интегрирования кинематических уравнений типа (7.5) могут быть построены для любого вида первичной информации об угловой скорости . Традиционные методики синтеза дискретных алгоритмов базируются на полиномиальном представлении обоих сомножителей в (7.6) на такте интегрирования.

Учитывая функциональную связь этих сомножителей в данном случае, для построения дискретного алгоритма фактически используется разложение в ряд только вектора . Искомый интеграл представляется через коэффициенты полиномиальной модели , которые выражаются в свою очередь через выходные сигналы гироскопов . В современных БИИМ на лазерных гироскопах и ВОГ с обратной связью первичная информация получается в виде угловых квазикоординат (проекций приращений угла поворота на связанные оси). Значения составляющих вектора «считывается» при опросе датчиков с тактом в определенные моменты времени . При этом частота опроса гироскопов выбирается кратной частоте решения задачи. Количество коэффициентов полиномиальной модели , которые могут быть определены, равно количеству выходных сигналов гироскопов, доступных на интервале интегрирования.

Особенность аппроксимации функций , интерполяционными полиномами в виде ряда по степеням состоит в том, что интерполяция выполняется внутри шага, т.е. на интервале по получении последнего значения .

Для получения дискретного алгоритма решения уравнения (7.6) представим вектор Эйлера в виде разложения в ряд Тейлора относительно точки

, (7.7)

и аппроксимируем изменчивость квазикоординат на интервале времени временным полиномом, например, для высокодинамичных объектов полиномом третьего порядка вида (квадратичная модель для вектора ) [1,2]:

(7.8)

где - постоянные на рассматриваемом интервале времени векторы.

Далее, полагая без потери общности, что , и дифференцируя (7.8) по времени, получим следующие соотношения для момента времени :

(7.9)

Дифференцирование уравнения (7.6) по времени и учет соотношений (7.9), а также, что , дает для момента времени :

(7.10)

Подставляя (7.10) в уравнение (7.7), получим

. (7.11)

Для нахождения постоянных на интервале интегрирования векторов весь интервал разобьем на три равных части и будем считать, что имеются значения квазикоординат в моменты времени , которые можно обозначить через ,, соответственно, причем ++.

Подставляя эти значения в (7.8), имеем три уравнения вида

(7.12)

которые позволяют найти значения векторов на шаге . После подстановки найденных значений векторов в уравнение (7.11) окончательно получим известный алгоритм Р.Миллера [1] для определения приращения вектора Эйлера на шаге через значения квазикоординат ,,, являющихся соответствующими интегралами выходных сигналов ДУС в виде

(7.13)

где , а .

При этом локальная погрешность вычисления вектора ориентации характеризуется следующим выражением

.

Отметим, что использованный выше метод позволяет получить алгоритмы более низких порядков. Так, если предположить, что квазикоординаты, т.е. интегралы от вектора угловой скорости изменяются в соответствии с квадратичным законом на интервале интегрирования (линейная модель для вектора ), то в уравнении (7.8) вектор , а вместо уравнения (7.11) получим

(7.14)

Далее, если обозначить , - соответствующие векторы квазикоординат в середине и конце интервала интегрирования, причем +, то можно вычислить новые значения для постоянных векторов и, подставляя их в уравнение (7.14), получить алгоритм второго порядка или так называемый алгоритм предварительной обработки информации Джордана

(7.15)

Если использовать вектор квазикоординат, полученный на целом интервале интегрирования, и вектор квазикоординат на предыдущем интервале интегрирования, то результирующий вектор Эйлера будет иметь вид [1]

. (7.16)

Наконец, предположение о том, что вектор квазикоординат на интервале интегрирования является линейной функцией (что эквивалентно предположению, что угловая скорость постоянна по величине и направлению) приводит к следующему решению

(7.17)

Рассмотрим решение кинематического уравнения (7.5) для вектора Эйлера, приведенное в [3]. Решение этого уравнения ищется на ограниченном шаге интегрирования методом малого параметра. Считая и величинами первого порядка малости, представим решение в виде

. (7.18)

Уравнения для получаются подстановкой (7.18) в исходное уравнение (7.5) и приравниванием членов одинакового порядка малости:

;

;

;

. (7.19)

Далее необходимо выполнить интегрирование полученных соотношений. Положим без уменьшения общности . Тогда в момент имеем

,

,

.

Или окончательно получим

, (7.20)

где

;

;

.

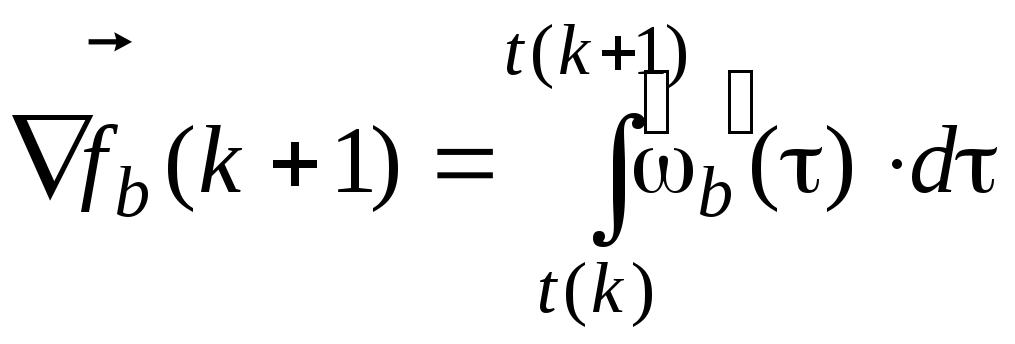Удерживая в решении (7.20) только первый член, получаем численный метод, который принято называть методом средней скорости. Удерживая первый и второй члены, получаем метод 3-го порядка, первый, второй и третий члены - метод 4-го порядка.

В работе [2] предложен дискретный алгоритм для пошагового интегрирования кинематического уравнения (7.5) для вектора Эйлера, основанный на использовании первичной информации о квазикоординатах, представляющих собой кратные интегралы от угловой скорости на шаге опроса датчиков.

При использовании первичной информации о квазикоординатах в виде первого и второго интегралов от угловой скорости

,

(7.21)

данный алгоритм 4-го порядка относительно имеет следующий вид:

. (7.22)

Основным достоинством алгоритма (7.22) в отличие от традиционных, является то, что он обладает одинаковой точностью вычислений как в условиях конического, так и произвольного углового движения объекта.

Приведем рекуррентный алгоритм задачи ориентации

при использовании дискретного алгоритма 4-го порядка

Fb=dfb+(1/12)*DFb*d2fb+(1/24)*DFb*d3fb [3]

для вычисления вектора Эйлера Fb на интервале интегрирования dT по квазикоординатам dfb=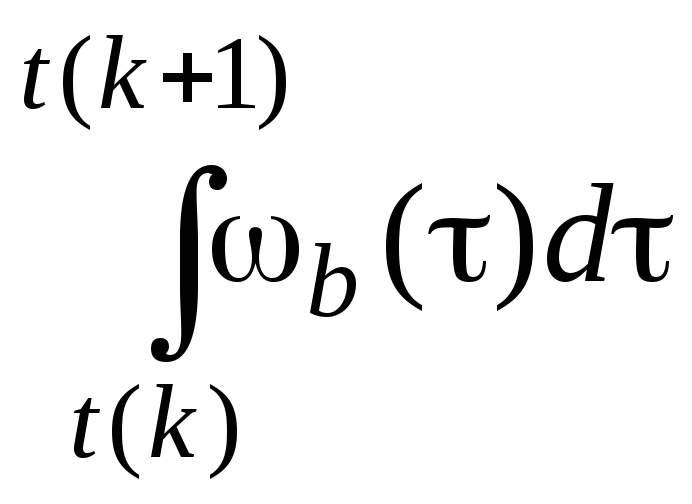 (приращениям угла поворота на шаге dT).

%Итак:

[dfxb_;dfyb_;dfzb_]=dfb_; - % исходные измерения (значения квазикоординат в осях чувствительности ДУС);

dfb(k+1)=(1 – (DMgo+FKDMg(k)))*dfb_(k+1) -

- (DGo+FKCDr(k))*dT+

+ [ 0 Tet_gxz (-1)*Tet_gxy;

(-1)*Tet_gyz 0 Tet_gyx;

Tet_gzy (-1)*Tet_gzx 0 ]*dfb_(k+1);

где DMgo –априорные оценки погрешностей масштабных коэффициентов ДУС с учетом температурных поправок; DGo – паспортные значения дрейфов; Tet_gij - паспортные значения неортогональностей измерительных осей (малые углы, характеризующие погрешности выставки измерительных осей ДУС относительно трехгранника , причем индекс указывает ось чувствительности, а индекс - ось, вокруг которой ось чувствительности повернута; FKCDr, FKDMg – текущие оценки из ФК;

[dfxb;dfyb;dfzb]=dfb(k+1);

DFb=[ 0 (-1)*dfzb dfyb;

dfzb 0 (-1)*dfxb;

(-1)*dfyb dfxb 0 ];

d2fb(k+1)=dfb(k+1) - dfb(k);

d3fb(k+1)=d2fb(k+1) – d2fb(k);

Fb=dfb+(1/12)*DFb*d2fb+(1/24)*DFb*d3fb;

[Fx;Fy;Fz]=Fb;

%Формирование кватерниона HH(i,b)

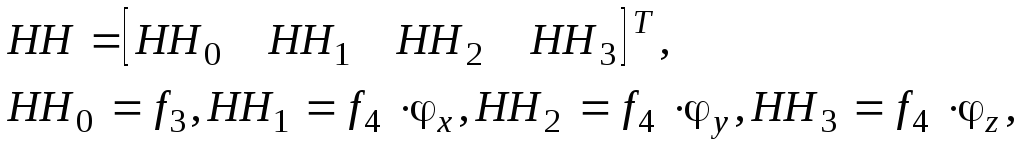
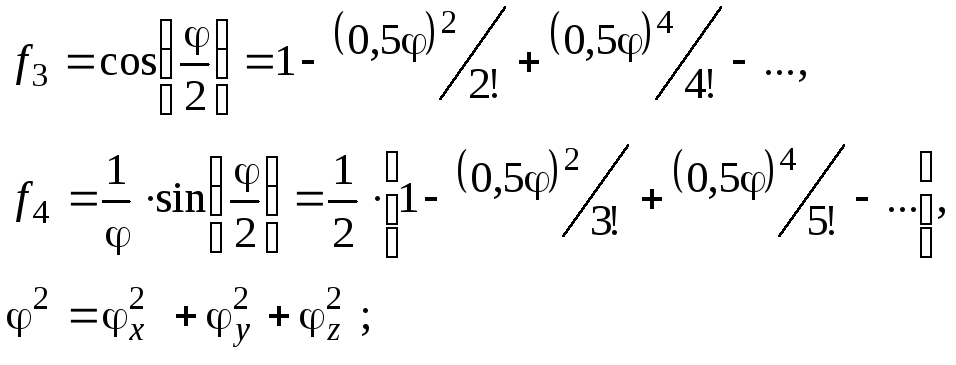
здесь .

Или

F2=(Fx^2+Fy^2+Fz^2)/4;

F3=(6-F2)/12+(F2^2)/240;

HH=[1-F2/2+(F2^2)/24;

F3*Fx;

F3*Fy;

F3*Fz];

%Формирование вектора Эйлера Fh по Om(h)_(k).

% Fh(k+1)=dfh+(1/12)*DFh*d2fh+(1/24)*DFh*d3fh;

[OmE_;OmN_;OmH_]=Omh_(k);

OmE=OmE_ - (1/Tz)*beta;

OmN=OmN_ - (1/Tz)*gamma;

OmH=OmH_ - (1/Tz)*alpha;

Omh(k)=[OmE;OmN;OmH];

dfh(k+1)=Omh(k)*dT;

[dfE;dfN;dfH]=dfh;

DFh=[ 0 (-1)*dfH dfN;

dfH 0 (-1)*dfE;

(-1)*dfN dfE 0 ];

d2fh(k+1)=dfh(k+1) - dfh(k);

d3fh(k+1)=d2fh(k+1) – d2fh(k);

Fh=dfh+(1/12)*DFh*d2fh+(1/24)*DFh*d3fh;

[FE;FN;FH]=Fh;

%Формирование кватерниона FF(h,i)

F4=(FE^2+FN^2+FH^2)/4;

F5=(6-F4)/12+(F4^2)/240;

FF=[1-F4/2+(F4^2)/24;

(-1)*F5*FE;

(-1)*F5*FN;

(-1)*F5*FH];

[FFO;FFE;FFN;FFH]=FF;

%Формирование кватерниона Lhb(k+1)

MFF=[FFO (-1)*FFE (-1)*FFN (-1)*FFH;

FFE… FFO (-1)*FFH FFN;

FFN FFH FFO (-1)*FFE;

FFH (-1)*FFN FFE FFO];

FFL(k+1)=MFF(k+1)*L(k);

[FFLO;FFL1;FFL2;FFL3]=FFL;

MFFL=[FFLO (-1)*FFL1 (-1)*FFL2 (-1)*FFL3;

FFL1… FFLO (-1)*FFL3 FFL2;

FFL2 FFL3 FFLO (-1)*FFL1;

FFL3 (-1)*FFL2 FFL1 FFLO];

L_(k+1)=MFFL(k+1)*HH(k+1);

[L1_;L2_;L3_;L4_]=L_(k+1);

mL_^2=L1_^2+L2_^2+L3_^2+L4_^2;

L(k+1)=L_(k+1)+(1/2)*(1-mL_^2)*L_(k+1);

%Формирование матрицы Cbh(k+1)

[L1;L2;L3;L4]=L(k+1);

c11=L1^2+L2^2 - L3^2 - L4^2;

c12=2*(L2*L3 – L1*L4);

c13=2*(L2*L4+L1*L3);

c21=2*(L2*L3+L1*L4);

c22=L1^2+L3^2 – L2^2 - L4^2;

c23=2*(L3*L4 – L1*L2);

c31=2*(L2*L4 – L1*L3);

c32=2*(L3*L4+L1*L2);

c33=L1^2+L4^2 – L2^2 – L3^2;

Cbh=[c11 c12 c13;

c21 c22 c23;

c31 c32 c33]; (7.23)

Значения углов вычисляются из значений элементов матрицы

,

(где - матрица направляющих косинусов, определяющая ориентацию связанной с ИБ системы координат относительно связанной с корпусом объекта системы координат )

по формулам (6.22)…(6.25) (см. Л6).

О вычислительных дрейфах в БИИМ на ДУС

Методические погрешности алгоритмов ориентации традиционно оценивают в условиях заданного тестового движения основания.

Известно, что наибольшие вычислительные погрешности определения параметров ориентации в БИИМ на ДУС возникают при так называемом коническом движении объекта, при котором они характеризуются вычислительным дрейфом, содержащим постоянную составляющую вдоль оси, которая описывает конус. Т.е. локальные (на шаге интегрирования) вычислительные погрешности являются константами, не зависящими от такта решения задачи.

Вычислительный дрейф, возникающий при реализации в вычислителе БИИМ дискретных алгоритмов выработки параметров ориентации, является одной из основных особенностей БИИМ, построенных на ДУС. Поясним природу такого дрейфа и дадим его качественные и количественные оценки.

Пусть взаимное положение опорного (неподвижного) трехгранника и связанного (подвижного) трехгранника определяется поворотом вокруг линии , лежащей в плоскостях и , на угол (рис.7.1). Если линия вращается с угловой скоростью вокруг оси , то ось будет описывать коническую поверхность, причем осью этого конуса будет ось , половина угла при вершине будет , а оси и будут участвовать в колебательных движениях вокруг осей и соответственно.

Рис.7.1. Коническое движение

Модуль вектора поворота, описывающего вращение, в результате которого опорные оси совмещаются со связанными, равен , а направлен этот вектор вдоль оси . Если выбран произвольный начальный момент времени, причем направлена вдоль оси , то вектор Эйлера имеет составляющие .

Поэтому кватернион , составленный из параметров Родрига-Гамильтона и определяющий ориентацию подвижного трехгранника относительно опорного имеет вид

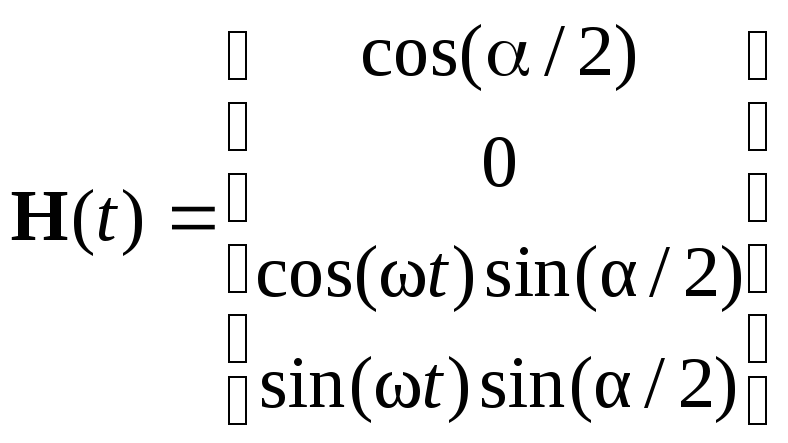. (7.24)

Пусть кватернион представляет собой вращательное движение тела из положения в момент времени , в положение в момент . Тогда

, (7.25)

где () – оператор «умножения» кватернионов. Из (7.25) непосредственно следует, что ,т.е.

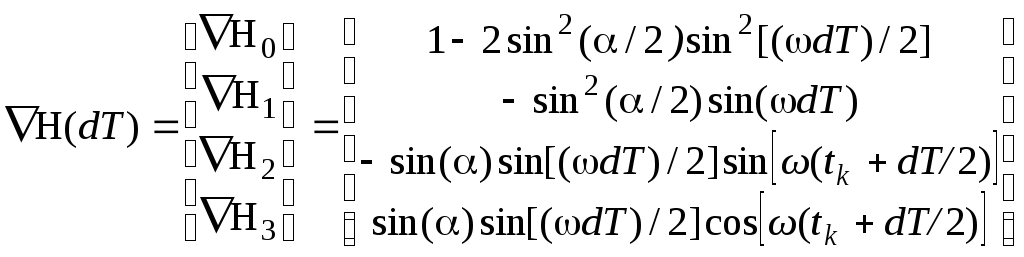. (7.26)

Составляющие вектора угловой скорости вращения подвижного трехгранника на свои оси могут быть найдены из дифференциального уравнения, которое описывает поведение кватерниона и имеет вид

. (7.27)

или

Из (7.27) имеем и

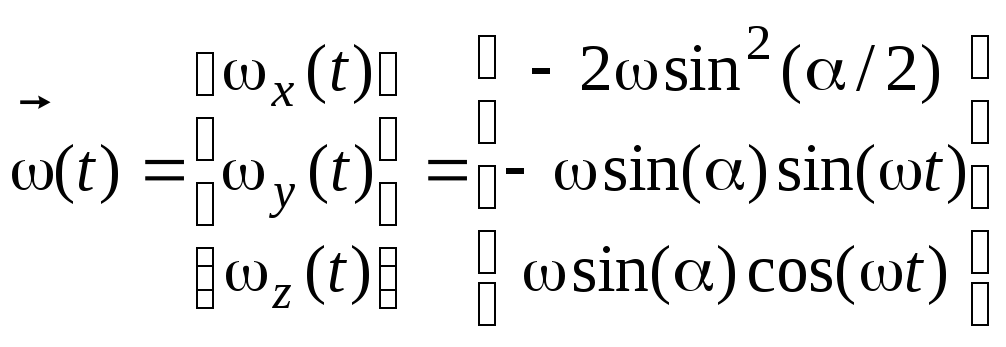. (7.28)

Наконец, интегрируя (7.28) в интервале времени от момента до , получим значения квазикоординат в виде

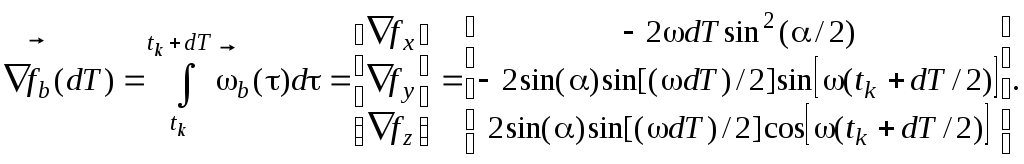(7.29)

Соотношение (7.29) позволяет рассчитать вектор Эйлера для случаев, рассмотренных выше на интервале времени от до :

1) по формуле (7.13) при использовании трех интегралов от угловой скорости;

2) по формулам (7.15) и (7.16) при использовании двух интегралов от угловой скорости;

3) по формуле (7.17) при использовании одного интеграла от угловой скорости.

Также оно дает возможность получить для этих случаев значение так называемого вычислительного дрейфа на шаге интегрирования как разность точного и вычисленного по этим формулам значения компонент вектора . Так, для конусного движения тела с малым углом при вершине конуса в работе [1] приведены следующие значения для вычислительного дрейфа при определении вектора :

• по формуле (7.13)

, (7.30)

• по формуле (7.15)

, (7.31)

• по формуле (7.16)

, (7.32)

• по формуле (7.17)

. (7.33)

Значения вычислительного дрейфа в условиях углового движения основания, типичного для объектов ракетной техники, приведены в табл. 7.1

Табл. 7.1

Условия расчета	Вычислительный дрейф (град/ч) при определении вектора по формуле
	(7.13)	(7.15)	(7.16)	(7.17)
=10, = 1 рад/с, dT= 510-3 c	0	410-9	610-8	710-3
=10, = 1 рад/с, dT= 510-2 c	310-14	610-8	110-6	510-2
=10, = 0,8 рад/с, dT= 510-3 c	0	110-9	210-8	610-3
=10, = 0,8 рад/с, dT= 510-2 c	610-15	210-8	310-7	310-2
=1,0, = 10 рад/с, dT= 510-3 c	510-11	410-6	610-5	110-1

Алгоритмы, выведенные с использованием общей методики, могут быть оптимизированы под коническое движение путем специальной «настройки» коэффициентов алгоритма без изменения его структуры.

Известно несколько методик оптимизации алгоритмов ориентации. Исходная была предложена Р.Миллером в 1983г. Она предполагает получение аналитического выражения для погрешности алгоритма в виде ряда по степеням ( - круговая частота конического движения) с последующим определением считающихся неизвестными коэффициентов из условия «зануления» высших членов ряда [1].

Следует также отметить известное положение о том, что в условиях конического движения оптимизированные алгоритмы ориентации на 2 порядка точнее соответствующих неоптимизированных алгоритмов. В тоже время алгоритмы, оптимизированные под коническое движение, в условиях произвольного углового движения обладают более низкой точностью, уступая соответствующим неоптимизированным алгоритмам. Т.е. на практике это означает, что при использовании оптимизированных алгоритмов уровень методических вычислительных погрешностей может существенно возрастать в процессе интенсивного маневрирования подвижного объекта.

Наиболее эффективным средством повышения точности алгоритмов ориентации является увеличение частоты опроса гироскопов.