Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тамбовский Государственный Университет им. Г.Р. Державина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математическое моделирование / belova

.pdf

Скачиваний:

Добавлен:

20.03.2016

Размер:

633.17 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 98 9 > Следующая >>>

Метод граничных элементов для решения уравнений в частных
производных	71

Фундаментальным решением этого уравнения называется решение урав• нения вида

∂2u	+	∂2u	+ δ(ξ − x) (η − y) = 0.	(4.193)
∂x2		∂y2

Надо найти решение уравнения Лапласа в двумерной области, имею• щее сингулярность в точке (ξ, η). Это решение должно быть симметрично относительно точки (ξ, η), поэтому мы введем полярную систему координат с центром в точке сингулярности, тогда

r = q

(ξ − x)2 + (η − y)2

(4.194)

Оператор Лапласа запишется в виде

1 ∂

∂ω

1 ∂2ω

ω =

(4.195)

∂r

∂θ2

Для r > 0 δ(ξ − x, η − y) = 0; учитывая симметрию задачи, уравнение можно записать в виде

Учитывая симметрию задачи, уравнение можно записать в виде

1 ∂	r	∂ω	= 0.	(4.196)

r ∂r		∂r

Это уравнение можно решить при помощи обычного интегрирования, решение будет иметь вид:

ω = A log r + B

(4.197)

Эта функция сингулярна в точке r = 0. Для нахождения A и B вос• пользуемся свойствами дельта-функции.

Z	Z
r2ωdD = −	δdD = −1.	(4.198)

Здесь D — любая область, содержащая точку r = 0. Для оценки ин• тересующих нас интегралов мы рассмотрим простую область — круг с центром в точке r = 0 и радиусом > 0 (см. рис. 24).

При помощи теоремы Грина–Гаусса оценим интеграл

Z r2ωdD = Z	∂n dS =
	∂ω

D∂D

72	Детерминированное моделирование

Рис. 24.

= Z	∂r dS =	2π = 2πA.	(4.199)
	∂ω	A

∂D

Мы преобразовали интеграл по площади в интеграл по границе; т. к. область D — круг, то нормаль n направлена по радиусу. Отсюда получаем:


A	= −		1	,	(4.200)
			2π
ω = −	1	log r + B.			(4.201)

	2π

B принимает произвольные значения, но обычно полагается равным нулю; таким образом, фундаментальное решение для уравнения Лапласа для двумерной области имеет вид:

ω = −	1	log r =	1	1
				log		,	(4.202)
	2π		2π		r

причем

Метод граничных элементов для решения уравнений в частных

производных		73
r = q
r = q	(ξ − x)2 + (η − y)2	(4.203)

Аналогичным образом находится фундаментальное решение для трех•

мерного уравнения Лапласа, оно имеет вид:
ω =	1	(4.204)
	4πr

Метод граничных элементов для двумерной задачи

Рассмотрим применение метода граничных элементов для решения урав• нения Лапласа в двумерной области. Сначала, также как в методе ко• нечных элементов, запишем интегральное уравнение и применим теорему Грина–Гаусса:

0 = ΩZ	r2u.ωdΩ =∂ZΩ	∂nωd −	ΩZ	ru.rωdΩ.	(4.205)
		∂u

Затем применим теорему Грина–Гаусса еще раз ко второму интегралу в правой части

0 =∂ZΩ		∂nωd − ΩZ ru.rωdΩ =
		∂u
=∂ZΩ	∂nωd −∂ZΩ u		∂n d +	ΩZ	ur2ωdΩ.	(4.206)
	∂u		∂ω

В методе конечных элементов в качестве весовой функции выбиралась одна из базисных функций, которые использовались для аппроксимации решения (решение искалось в виде разложения по базисным функциям). В методе граничных элементов в качестве весовой функции используется фундаментальное решение уравнения Лапласа, полученное выше.


	1
	ω = −			log r,	(4.207)
			2π
	r = q
		(ξ − x)2 + (η − y)2
Используя свойства дельта-функции, получим:
Z	Z
	ur2ωdΩ = − uδ(ξ − x) (η − y)dΩ = −u(ξ, η),				(4.208)

ΩΩ

74	Детерминированное моделирование

где

(ξ, η) Ω

Здесь вместо интеграла по области получили значение функции в точке, и уравнение принимает вид:

Z	Z
ur2ωdΩ = −	uδ(ξ − x) (η − y)dΩ = 0.	(4.209)

ΩΩ

Таким образом, интегральное уравнение записывается в виде:

u(ξ, η) +∂ZΩ u ∂n d =∂ZΩ		∂nωd ,	(4.210)
	∂ω	∂u

где

(ξ, η) Ω

Это уравнение содержит только интегралы по границе. Если точка (ξ, η) находится вне Ω, то

Z	Z
ur2ωdΩ = −	uδ(ξ − x) (η − y)dΩ = 0.	(4.211)

ΩΩ

Если точка (ξ, η) лежит на границе области, то первый член предыду• щего уравнения заменяется выражением:

u(ξ, η)

Пусть P — точка с координатами (ξ, η) в области Ω. Чтобы оценить интеграл

ur2ωdΩ,

добавим в область Ω окружность радиусом вокруг точки P (точнее ее часть, выходящую за пределы области Ω) (см. рис. 25) и увеличенную область назовем Ω0, а ее границу 0.

0 = −

(4.212)

Теперь точка P находится внутри области 0 и мы можем написать

Метод граничных элементов для решения уравнений в частных
производных	75

Рис. 25.

u(P) +	Z	u ∂n d =		Z	∂nωd	(4.213)
			∂ω		∂u
	−			−

Нам надо рассмотреть предел этого выражения при → 0. Рассмотрим входящие в выражение интегралы

Z u ∂n d = Z		u∂n		−2π log r d =
	∂ω		∂	1


= Z	u∂r		−2π log r d = −2π Z						r d =
		∂			1			1	u
	= −2π Z
	= −2π Z					ud → −2π u(P)π ,				(4.214)
			1	1		1	1

следовательно

→0 Z u ∂n d =		→0	−2π		π = −	2
	∂ω			1 u(P)		u(P)
lim		lim					(4.215)

Аналогично

→0 Z	ω ∂nd =		→0	−2π ∂n (P)π log =
lim		∂u	lim	1	∂u	0	(4.216)

76	Детерминированное моделирование

Теперь осталось рассмотреть интегралы по − Если подынтегральные выражения достаточно «хорошие» (в противном случае надо рассматри• вать главные значения интегралов), то

→0

∂nωd

∂nωd = Z

lim

−

∂u

lim

∂ω

ud =

∂ω

(4.217)

∂n

→0

∂n

−

∂ω

∂u

u(P) + Z

d =

u(P) + Z

ωd ,

∂n

∂ω

∂u

u(P) + Z

d = Z

ωd

(4.218)

∂n

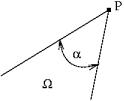
Полученное выражение справедливо, если граничная точка P «глад• кая» (в этой точке существует единственная производная); если точка P яв• ляется вершиной угла α, то коэффициент 1/2 заменяется α/2π (см. рис. 26)

Рис. 26.

Таким образом, мы получаем интегральное уравнение

c(P)u(P) + Z	u ∂n d = Z		∂nωd ,	(4.219)
		∂ω	∂u

где

Метод граничных элементов для решения уравнений в частных

производных						77
	1
	1				r = q(ξ − x)2 + (η − y)2,
ω = −			log r,
ω = −		2π	log r,
c(P) =	1/2,			P	и гладкая в т. P	(4.220)
	1,			P	Ω
	α/2π,			P	и не гладкая в т. P

Для трехмерной задачи уравнение получается такое же, но справедливы

следующие соотношения:
		1
ω =			,	r = q(ξ − x)2 + (η − y)2 + (γ − z)2,

	4πr
c(P) =		1/2,		P	и гладкая в т. P		(4.221)
		1,		P		Ω

α/4π, P и не гладкая в т. P

Вполученное нами уравнение входят значения u и ∂∂nu на границе и зна• чение u в точке P. Если значения u и ∂∂nu на границе известны, то значения u в точке P внутри области Ω могут быть найдены. Полученное уравнение

используется для нахождения значений u и ∂∂nu на поверхности, а затем, ес• ли необходимо, используется для нахождения решения в точках области.

Процедура численного решения интегрального уравнения мето• дом граничных элементов

Сначала область разбивается на граничные элементы.

Рис. 27.

78 Детерминированное моделирование

На рис. 27 (a) изображена сетка граничных элементов, а на рис. 27 (b)

— сетка конечных элементов. Используя разбиение границы на элементы

N	N				N
jS	N				N
( =	j), получим:
=1	c(P)u(P) + j=1	Z	u ∂n d = j=1			Z	∂nωd	(4.222)
	c(P)u(P) + j=1	Z	u ∂n d = j=1			Z	∂nωd	(4.222)
	X j			∂ω	X j		∂u
	X j				X j

На каждом элементе j введем стандартные базисные функции конеч•

ных элементов
X	∂uj		X
uj = ϕαujα,	qj ≡		= ϕαqjα,	(4.223)
uj = ϕαujα,	qj ≡	∂n	= ϕαqjα,	(4.223)
α			α

где uj, qj — значения u и q на граничном элементе j, где ujα, qjα — значения u и q в узле α элемента j. Базисные функции для u и q могут быть стандартными одномерными базисными функциями конечных элемен• тов (если мы решаем двумерную задачу, то мы должны интерполировать функции при помощи одномерных элементов). Обычно базисные функции для u и q берутся одинаковыми, но это не обязательно. Использование разложения по базисным функциям приводит к соотношению:

N	ujα Z		N	qjα Z	ϕαωd (4.224)
c(P)u(P) + j=1 α		ϕα ∂n d = j=1 α
X X		∂ω	X X
	j			j

Уравнение справедливо для любой точки P на границе . Пусть P сов• падает с i–тым узлом введенной сетки, тогда уравнение для i–того узла имеет вид:

N	ujα Z	ϕα ∂ni	N	qjα Z	ϕαωid	(4.225)
ciui + j=1 α			d = j=1 α
X X		∂ω	X X
	j			j

Здесь ωi — фундаментальное решение с сингулярностью в узле i. По• лученное уравнение можно записать в виде:

Xj	X	XX
ciui +	ujαaijα =	qjαbijα,	(4.226)
=1	α	j=1 α

где

Метод граничных элементов для решения уравнений в частных

производных					79
aijα = Z	ϕα ∂n d , bijα = Z			ϕαωid	(4.227)
	∂ωi
j			j
Затем соберем эти уравнения в матричную систему
		Au = Bq			(4.228)

Векторы u и q — векторы значений в узлах величин u и q. Если у нас L узлов, то получим L уравнений и L неизвестных. Необходимо преобра• зовать систему к следующему виду

Cx = f,

(4.229)

где x — вектор неизвестных. Систему можно решить стандартными методами линейной алгебры. Матрицы A и B (и, следовательно, C) пол• ностью определенные и несимметричные (в методе конечных элементов матрица жесткости симметрична и разрежена).

Решение в точке области P ищется следующим образом:

N	X	N
Xj	X	X X
u(P) =		qjαbPjα −	ujαaPjα	(4.230)
=1	α	j=1	α

Сравнение методов конечных и граничных элементов

1. КЭ: Требуется строить сетку во всей области задачи

ГЭ: Требуется строить сетку только на границе области Это одно из основных преимуществ метода граничных элементов.

2.КЭ: Решение ищется сразу во всей области

ГЭ: Сначала ищется решение на границе; решение во всей об• ласти, если это необходимо, ищется потом

Существует большое количество задач, для решения которых доста• точно найти только решение на границе, а решение во всей области не требуется.

3. КЭ: Значения производных на границе (потоков) находятся с меньшей точностью

ГЭ: Точность нахождения u и q — одинакова

4.КЭ: Используется аппроксимация самого дифференциального

уравнения

80	Детерминированное моделирование

ГЭ: Используется аппроксимация только граничных условий.

Вметоде граничных элементов используются теорема Грина–Гаусса и фундаментальные решения, аппроксимация самого уравнения внут• ри исследуемой области не проводится, аппроксимация используется только на границе.

5.КЭ: Матрица в получившейся алгебраической системе — раз•

режена и симметрична.

ГЭ: Матрица в получившейся алгебраической системе полно• стью заполнена и несимметрична.

Выбор наиболее подходящего метода частично зависит от соотноше• ния размера области и ее границы. Так, для задач, решающихся в бесконечных или полубесконечных областях, метод граничных эле• ментов предпочтительней.

6. КЭ: Интегралы, получающиеся в методе конечных элементов легко вычислить.

ГЭ: В методе граничных элементов возникают трудности при вычислении интегралов.

7.КЭ: Применим для широкого класса задач. Успешно решает

многие нелинейные задачи

ГЭ: Не всегда справляется даже с линейными задачами. Существует достаточно много задач, для которых не удается найти фундаментальных решений.

8.КЭ: Относительно легок в применении.

ГЭ: Применять гораздо труднее.

<<< < Предыдущая 1 2 3 4 5 6 78 / 98 9 > Следующая >>>

Соседние файлы в папке Математическое моделирование

#
20.03.201610.15 Mб77Arz_(2010)_Mathematical_&_Computer_Modelling.pdf
#
20.03.20167.31 Mб56Arz_Zen_(2010)_Artificial_Intellegence.pdf
#
20.03.2016633.17 Кб35belova.pdf