Математическое моделирование / belova

4.Детерминированное моделирование

Вэтом разделе рассматривается компьютерное моделирование с ис• пользованием детерминированных моделей. Рассматривается моделирова• ние различных процессов и явлений, для описания которых можно исполь• зовать алгебраические уравнения и системы, дифференциальные уравне• ния, уравнения в частных производных. В этом случае процесс моделиро• вания состоит в решении при помощи компьютера соответствующих урав• нений и систем. Как уже упоминалось, в данном пособии мы не будем по• дробно разбирать уже изученные вами способы решения алгебраических уравнений и систем, решение обыкновенных дифференциальных уравне• ний, а сконцентрируемся на решении на компьютере уравнений в частных производных.

4.1 Классификация дифференциальных уравнений в частных производных. Граничные и начальные условия

Дифференциальное уравнение в частных производных (ДУЧП):

Здесь U — зависимая переменная (функция), xi — независимые пе• ременные. Существенно то, что неизвестная функция U(xi) зависит более чем от одной переменной.

Порядком уравнения называется порядок старшей частной производ• ной.

Квазилинейное уравнение — уравнение, линейное относительно всех старших производных от неизвестной функции.

Линейное уравнение — уравнение, линейное относительно функции и всех ее частных производных.

Целью предлагаемого курса является решение квазилинейных ДУЧП второго порядка, содержащих две независимые переменные. При необхо• димости методы их решения могут быть обобщены на случай большего количества переменных. Под квазилинейностью будет пониматься линей• ность по всем частным производным. Общий вид такого уравнения:

Выделяют три типа ДУ второго порядка:

Эллиптические: AC − B2 > 0. Например, уравнение Пуассона

Гиперболические: AC − B2 < 0. Например, волновое уравнение

Параболические: AC − B2 = 0. Например, уравнение теплопровод• ности

Уравнение может принадлежать к нескольким типам в зависимости от

при y > 0 эллиптического типа, при y < 0 — гиперболического, а линия y = 0 называется линией параболичности.

Квазилинейное ДУЧП второго порядка:

A(x, y, U) ∂∂2xU2 + 2B(. . .) ∂∂x2∂Uy + C(. . .) ∂∂2yU2 + +D(. . .) ∂∂Ux + E(. . .) ∂∂Uy + f(x, y, U) = 0

Для однозначности решения подобного уравнения необходимо наложе• ние дополнительных условий. Эти условия бывают двух типов:

Начальные условия (НУ) — условия, определяющие значения иско• мой функции (и, возможно, некоторых ее производных) при одном значении независимой переменной (например, в начальный момент времени, т.е. при t = 0).

Если в уравнении присутствует только первая производная по времени (как в уравнении теплопроводности), то достаточно задать одно началь• ное условие, например, распределение температуры в начальный момент. Если же в уравнении присутствует вторая производная по времени (вол• новое уравнение), то необходимы два НУ, например, положение струны в начальный момент и скорость движения ее точек.

Граничные условия (ГУ) — условия, определяющие значения иско• мой функции (и, возможно, некоторых ее производных) на границе про• странственной области, внутри которой ищется решение (при различных значениях независимых переменных).

ГУ бывает трех типов:

Задаются значения функции на границе — задача Дирихле;

Задаются значения производной функции по нормали к границе — задача Неймана;

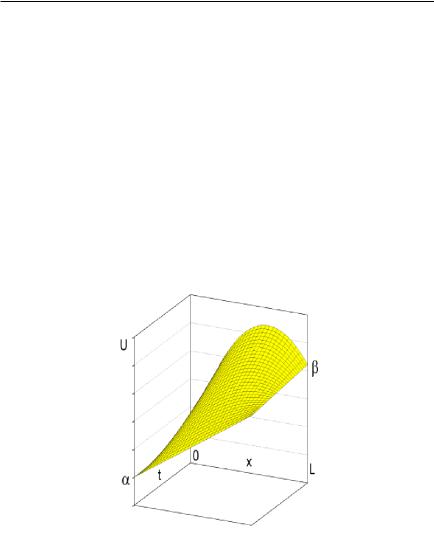
Геометрическая интерпретация задачи

Если независимых переменных всего две (например, x и t), то искомое решение можно изобразить в виде поверхности в трех измерениях U(x, t). (См. рис. 1). Граничные условия — линии в плоскостях x = 0 и x = L. Начальные условия — кривая в плоскости t = 0.

Рис. 1.

Основная идея метода конечных разностей[5] На область изменения независимых переменных накладывается сетка,

и решение ищется не в виде непрерывной функции U(x, t), а в виде дис• кретного, конечного множества чисел Uin, представляющих (заменяющих)

Рис. 2.

функцию U(x, t) на дискретном, конечном множестве значений независи• мых переменных, т.е. в узлах наложенной сетки. Мы ищем конечный дис• кретный набор чисел Uin над соответствующими узлами сетки.

Простейшей сеткой является равномерная прямоугольная сетка. Такая сетка образуется при пересечении линий x = xi = i · h, i = 0, 1, . . . , N и t = tn = n · τ, n = 0, 1, . . . (См. рис. 2). h — шаг сетки по координате, τ

— по времени.

Сходимость Множество Uin называют численным решением ДУ, если выполняется условие сходимости:

Двойными вертикальными линиями отмечена норма отклонения числен• ного (дискретного) решения от истинного решения. Норму отклонения над дискретным пространством узлов v можно ввести, например, так:

Чтобы посторить алгоритм численного решения ДУ, все производные в исходном ДУ должны быть заменены отношениями конечных разностей (отсюда название метода). Данная процедура называется аппроксимация поизводных.

Используя в дополнение к выбранному i–тому узлу наложенной сетки (i +1)–ый, получаем формулу правой аппроксимации первой производной:

Для оценки погрешности аппроксимации производной по этой формуле значения функции в соседних узлах необходимо представить в виде ряда Тейлора:

Погрешность O(h).

Формула правой аппроксимации первого порядка точности. Ана• логичная формула для аппроксимации производной по времени называется аппроксимацией вперед по времени.

Используя в дополнение к выбранному i–тому узлу наложенной сетки (i − 1)–ый, получаем формулу левой аппроксимации первой производной:

Для оценки погрешности аппроксимации производной по этой формуле значения функции в соседних узлах необходимо представить в виде ряда Тейлора:

Погрешность O(h).

Формула левой аппроксимации первого порядка точности. Ана• логичная формула для аппроксимации производной по времени называется аппроксимацией назад по времени.

Используя в дополнение к выбранному i–тому узлу наложенной сетки (i − 1)–ый и (i + 1)–ый, получаем формулу левой аппроксимации первой производной:

получаем формулу центральной аппроксимации первой производной:

Для оценки погрешности аппроксимации производной по этой формуле значения функции в соседних узлах необходимо представить в виде рядов Тейлора. Подставляя эти ряды, получим:

Погрешность O(h2).

Формула центральной аппроксимации первого порядка точно• сти. Аналогично строится формула центральной аппроксимации для про• изводной по времени.

Используя в дополнение к выбранному i–тому узлу наложенной сетки (i − 1)–ый и (i + 1)–ый, получаем формулу левой аппроксимации первой производной:

получаем формулу центральной аппроксимации второй производной:

Для оценки погрешности аппроксимации производной по этой формуле значения функции в соседних узлах необходимо представить в виде рядов Тейлора. Подставляя эти ряды, получим:

Погрешность O(h2).

Формула центральной аппроксимации второго порядка точно• сти.

Вместо двух соседних точек можно взять, например, две последующие точки. Вы тоже без труда решите систему и получите аппроксимационную формулу для второй производной. Однако погрешность аппроксимации в этом случае будет уже пропорциональна шагу h в первой степени, т.е. вы получите аппроксимационную формулу первого порядка точности. По этой причине всегда предпочтительнее использовать симметричные точки для построения формул аппроксимации. Хотя иногда по самым разным причинам полезным может оказаться и несимметричный выбор точек, на• пример, когда вы находитесь на краю сетки. Несимметричные разностные аппроксимации приходится строить также для аппроксимации ГУ 2–го и 3–го рода.

Для повышения точности аппроксимации производной необходимо ис• пользовать большее количество соседних точек.

Так, например, для второй производной помимо (i−1)–ого и (i+1)–ого узлов (стандартная формула центральной аппроксимации) можно исполь• зовать еще и (i − 2)–ой и (i + 2)–ой узлы:

Решая данную систему относительно коэффициента b, получаем более точную формулу центральной аппроксимации второй производной:

Для оценки погрешности аппроксимации производной по этой формуле значения функции в соседних узлах необходимо представить в виде рядов

применительно к определенному узлу наложенной сетки (i, j) все произ• водные заменяются разностными аналогами. Например,

В результате получается система линейных алгебраических уравнений, отделяющая значения искомой функции во всех узлах наложенной сетки.

Для наглядности строят трафарет(stencil) разностной схемы: на сет• ке отмечают узлы, задействованные в разностном аналоге исходного ДУ, примененного к (i, j)–му узлу, и подписывают численный множитель, с ко• торым значение исходной функции, соответствующее данному узлу, входит в разностную схему.

Рис. 3.

На рисунке 3 изображен трафарет разностной схемы, содержащей че• тыре узла. Три узла принадлежат слою j, и один — (j+1)–му слою. Это — двухслойная разностная схема (относительно переменной y). Бывают так• же трехслойные и более многослойные разностные схемы.

Если трафарет содержит одно неизвестное значение функции U (на рисунке 3 это — Uij+1), то разностная схема называется явной. Система алгебраических уравнений при этом распадается на отдельные уравнения, каждое из которых явным образом определяет значение искомой функции в одном из узлов наложенной сетки.

Если трафарет содержит более одного неизвестных значений функции U, то разностная схема называется неявной. Система алгебраических урав• нений при этом не распадается на отдельные уравнения.

4.2 Методы конечных разностей для решения уравнений в частных производных

Решение уравнения Пуассона методом конечных разностей

Рассмотрим в качестве примера решение уравнения Пуассона методом конечных разностей [6].

Здесь ρ(x, y) — плотность заряда в среде.

Рассмотрим решение уравнения (4.26) конечно-разностным методом. Мы представляем функцию u(x, y) значениями в узлах прямоугольной сет• ки

где δ — шаг сетки (одинаковый и по x, и по y). Вторые производные можно заменить следующими выражениями

Чтобы записать систему линейных уравнений в матричной форме, пе• ренумеруем точки двумерной сетки одномерной последовательностью

Оно справедливо для внутренних точек области j = 1, 2, . . . , J − 1; l = 1, 2, . . . , L − 1

Граничные точки области, в которых заданы функции или производные, приведены ниже

Всю эту информацию (о значениях на границе) перенесем в правую

a(x, y) ∂∂x2u2 + b(x, y) ∂∂xu + c(x, y) ∂∂y2u2 + d(x, y) ∂∂yu +

(4.34)

+e(x, y) ∂∂x2∂uy + f(x, y)u = g(x, y)

Использование разностной схемы для этого уравнения приводит к ал• гебраической системе с матрицей аналогичной описанной выше.

Существуют три различных подхода к решению уравнения (4.33): мето• ды релаксации, «быстрые методы» [6] (методы Фурье) и прямые матричные методы. Методы релаксации явно используют структуру разреженной мат• рицы A. Матрица делится на две части

Где E легко инвертируется, а F — то что осталось, тогда:

При использовании метода релаксации сначала выбирается начальное приближение, а затем итеративно вычисляется следующее

Матрица, обратная к матрице E, легко находится, так что итерации быстрые, подробнее метод релаксации рассмотрим позже.

Так называемые быстрые методы (методы Фурье) применимы только для специального класса уравнений: с постоянными коэффициентами, или, в более общем случае, к уравнениям с разделяющимися переменными. Кро• ме того, границы области должны совпадать с линиями сетки. Заметим однако, что существуют многосеточные методы релаксации, которые могут быть быстрее «быстрых» методов.

При помощи матричных методов прямо решают уравнение