
Математическое моделирование / belova
.pdf
Метод конечных элементов для решения уравнения в частных |
|
производных |
61 |
3.Аппроксимация конечными элементами. Разделим область 0 < x < 1 на три элемента равной длины и заменим u(x) внутри каждого эле• мента при помощи конечно-элементной аппроксимации
u(ξ) = ϕ1 (ξ)u1 + ϕ2 (ξ)u2 |
= ϕn (ξ)un, |
(4.156) |
|
x(ξ) = ϕ1 (ξ)x1 + ϕ2 (ξ)x2 = ϕn (ξ)xn |
|||
|
|||
При использовании линейных базисных функций ϕ1 (ξ) = 1 − ξ, ϕ2 (ξ) = ξ. Далее используем аппроксимацию Галеркина ω = ϕm.
Интеграл по рассматриваемой области можно представить в виде сум• мы интегралов по каждому конечному элементу:
1 |
1 |
2 |
1 |
3 |
3 |
Z0 |
· dx = Z0 |
· dx + Z1 |
· dx + Z2 |
· dx |
(4.157) |
|
|
3 |
3 |
|
|
Перейдем в интегралах от интегрирования по x к интегралам по ξ:
|
|
|
|
x2 |
1 |
|
|
|
|
|
Z |
Z |
|
|
|
|
|
· dx = |
·J dξ |
(4.158) |
|
|
|
|
x1 |
0 |
|
J = dx |
|
, J — якобиан перехода от x координат к ξ координатам. |
||||
|
dξ |
|
|
по элементам. Интегралы в левой части уравнения име• |
||
4. Интегралы |
||||||
|
|
|
|
|
|
|
ют вид: |
|
|
|
|
|
|
1
Z0 |
du dω |
|
(4.159) |
kdx dx |
J dξ |
Здесь u = ϕnun, ω = ϕm и уравнение принимает вид:
1 |
kddξm dx dξn dx + ϕmϕn J dξ |
(4.160) |
|
un Z0 |
|||
|
|
ϕ dξ dϕ dξ |
|
Заметим, что x(ξ) = ϕnXn, x = 13 ξ, J = ddxξ = 13 .
Матрица, на которую умножается un называется матрицей жесткости:
Emn = |
1 |
kddξm |
dx dξn |
dx + ϕmϕn J dξ = |
(4.161) |
01 |
|||||
|
R |
ϕ |
dξ dϕ |
dξ |
|
|
|
|
|
|
= R kddϕξm 3ddϕξn 3 + ϕmϕn) 13 dξ
0

62 |
Детерминированное моделирование |
Чтобы найти матрицу, подставим базисные функции и их производные ϕ1 (ξ) = 1 − ξ ddϕξ1 = −1, ϕ2 (ξ) = ξ ddϕξ2 = 1. Тогда получим
|
1 |
9k |
|
|
2 |
|
|
dξ = |
|
E11 |
= 3 0 |
dξ1 |
|
+ (ϕ1) |
|
||||
|
R1 |
|
dϕ |
|
|
2 |
(4.162) |
||
|
1 |
|
|
|
|
|
|
||
|
= 31 R0 |
|
9k(−1)2 + (1 − ξ)2 dξ = 31 9k + 31 |
||||||
Аналогично,
E12 = E21 = 31 |
|
−9k + 61 |
, |
|
|
|
|||||||||
|
E22 |
= 1 |
|
|
1 |
|
, |
|
|
|
|
|
|||
|
|
|
|
9k + |
9k + |
|
|
(4.163) |
|||||||
Emn = 1 |
1 |
|
9k +3 |
1 |
|
13 |
|
1 |
|
||||||
3 |
|
9k + 1 |
3 |
1 |
9k + 1 |
6 |
! |
||||||||
|
|
|
|
3 |
|
|
− |
|
|
|
|
||||
3 |
− |
|
6 |
|
3 |
|
|
|
3 |
|
|
||||
5. Ансамблирование
Рис. 18.

Метод конечных элементов для решения уравнения в частных
производных |
|
|
|
|
|
|
63 |
|
28 |
− |
53 |
0 |
0 |
U1 |
|
9 |
18 |
|
−1853 |
289 + 289 |
−1853 |
|||
|
|
|
|
|
|
|
|
0 |
|
53 |
28 |
+ 28 |
|
|
|
− |
18 |
9 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
53 |
|
|
− |
18 |
||||
|
|
|
|
|
||
|
|
|
|
0U2
|
18 |
U3 |
|
(4.164) |
||
− |
|
|
|
|
|
|
|
53 |
|
|
|
|
|
28 |
|
U |
4 |
|
|
|
9 |
|
|
|
|
||
|
|
|
|
|
|
|
Решение двумерной и трехмерной стационарной задачи теплопроводности методом конечных элементов
Трехмерное стационарное уравнение теплопроводности можно записать в виде:
−∂x |
kx ∂x |
− |
∂y |
ky ∂y |
− |
∂z |
kz ∂z |
= 0 |
(4.165) |
||||
|
∂ |
|
∂u |
|
∂ |
|
∂u |
|
∂ |
|
∂u |
|
|
Здесь kx, ky, kz — коэффициенты теплопроводности вдоль осей x, y, z. В случае постоянных коэффициентов теплопроводности уравнение запи• сывается в виде −r·(kru) = 0. Если же коэффициенты теплопроводности одинаковы по всем направлениям, то уравнение принимает вид: kr2u = 0. Мы должны решит уравнене в области Ω с границей (рис. 19).
Рис. 19.
Интегральное уравнение соответствующее этому уравнению можно за• писать следующим образом[7]:
Z
−r · (kru)ω dΩ = 0 |
(4.166) |
Ω
При помощи формулы Грина–Гаусса (аналог формулы интегрирования по частям):
64 |
|
|
Детерминированное моделирование |
|||||
|
ΩZ |
(fr · rg + rf · rg) dΩ = Z |
f ∂n d |
(4.167) |
||||
|
|
|
|
|
∂ g |
|
||
Уравнение можно переписать в виде |
|
|
|
|
|
|||
ΩZ |
−r · (kru)ω dΩ = ΩZ |
kru · rω dΩ − Z |
k∂nω d |
(4.168) |
||||
|
|
|
|
|
|
∂u |
|
|
В отсутствие правой части (нет источников тепла) уравнение имеет вид
Z |
kru · rω dΩ = Z |
k∂nω d |
(4.169) |
|
|
|
|
∂u |
|
Выражение под знаком интеграла в левой части можно представить в виде
ru · rω = |
∂u |
· |
∂ω |
= |
|
∂u ∂ξi |
· |
∂ω ∂ξj |
(4.170) |
||||
|
|
|
|
|
|
|
|
|
|||||
∂xk |
∂xk |
∂ξi ∂xk |
∂ξj ∂xk |
||||||||||
u и ω представляются в виде u = ϕnun, ω = ϕm. Здесь предполагается суммирование по одинаковым индексам.
Производные переменных «математического» пространства (0 < ξ < 1) по «физическим» переменным x и y определяются следующим образом:
|
∂ξ |
∂ξ |
|
|
|
|
|
∂ |
|
|
|
|
∂ |
− |
1 |
|
|
|
|
|
|
|
|||
∂x1 |
∂y1 |
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||
= |
∂ξ1 |
|
|
∂ξ2 |
|
|
= |
|
|
|
|
|
|||||||||||||
|
∂x2 |
∂y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.171) |
||||
|
∂ξ1 |
|
|
|
∂ξ2 |
|
∂y |
|
|
∂x |
|||||||||||||||
|
∂ξ |
∂ξ |
|
|
|
|
|
∂y |
|
|
|
|
∂y |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
= 1/ |
∂ξx |
∂ξ |
|
|
∂ξx |
|
∂ξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
∂ |
∂y |
− |
|
∂ |
|
∂y |
· |
|
|
∂ξ2 |
−∂ξ2 |
|
||||||||||
|
|
1 |
|
|
2 |
2 |
|
|
1 |
|
|
∂y |
|
∂x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ξ1 |
|
∂ξ1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
||
Представим область, в которой мы ищем решение, в виде совокупности элементов
I |
|
i[ |
(4.172) |
Ω = Ωi |
|
=1 |
|
Вкаждом элементе u можно представить в виде u = ϕnun = ϕ1u1 +
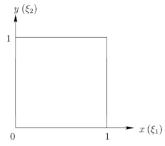
+ϕ2u2 +· · ·+ϕN uN . Отобразим каждый элемент на плоскость (ξ1, ξ2), как представлено на рисунке 20.

Метод конечных элементов для решения уравнения в частных |
|
производных |
65 |
Рис. 20.
Для каждого элемента базисные функции и их производные имеют вид:
ϕ1 = (1 − ξ1) (1 − ξ2) |
∂ϕ1 |
= − (1 − ξ2) , |
∂ϕ1 |
= − (1 − ξ1) |
|
∂ξ1 |
∂ξ2 |
||||
ϕ2 = ξ1 (1 − ξ2) |
|
∂ϕ2 |
= 1 − ξ2, |
∂ϕ2 |
= −ξ1 |
∂ξ1 |
∂ξ2 |
||||
ϕ3 = (1 − ξ1) ξ2 |
|
∂ϕ3 |
= −ξ2, |
∂ϕ3 |
= 1 − ξ1 |
∂ξ1 |
∂ξ2 |
||||
ϕ4 = ξ1ξ2 |
|
∂ϕ4 |
= ξ2, |
∂ϕ4 |
= ξ1 |
∂ξ1 |
∂ξ2 |
||||
(4.173)
Интегральное уравнение в случае двумерной задачи имеет вид:
ΩZ |
k ∂x ∂x |
+ ∂y ∂y |
dΩ = Z |
k∂nω d |
(4.174) |
|||
|
|
∂u ∂ω |
|
∂u ∂ω |
|
|
∂u |
|
Используя представление решения в виде разложения по базисным функциям и базисную функцию в качестве весовой функции, получим
P |
|
R |
|
|
|
|
un |
∂ϕn ∂ϕm |
+ |
∂ϕn ∂ϕm |
|||
∂u |
∂y |
(4.175) |
||||
i |
|
Ω |
|
|
|
|
R
= k∂n ϕn d Emnun = Fm
Emn — матрица жесткости, а Fm — вектор нагрузки m = 1, . . . , 4 и = = 1, . . . , 4.
66 |
Детерминированное моделирование |
Рис. 21.
Рассмотрим распределение тепла в единичном квадрате (см. рисунок 21). В этом случае элемент E11 имеет вид:
E11 |
1 |
1 |
|
(4.176) |
= k Z Z (1 − y)2 + (1 − x)2 dxdy = 3k |
||||
|
|
2 |
|
|
00
Аналогично вычисляются остальные элементы матрицы жесткости. Заметим, что если элемент не является единичным квадратом, нам надо
переходить от координат (x, y) к координатам (ξ1, ξ2). В этом случае надо в интеграл добавить якобиан перехода, т. е. использовать соотношение:
∂ϕn |
= |
∂ϕn ∂ξ1 |
+ |
∂ϕn ∂ξ2 |
= |
∂ϕn ∂ξi |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
∂x |
|
∂ξ1 ∂x |
∂ξ2 ∂x |
|
∂ξi ∂x |
|||||||||
|
|
|
|
|
||||||||||
Для единичного квадрата матричное уравнение имеет вид:
|
|
|
2 |
− |
1 |
− |
1 |
− |
1 |
|
|
|
|
|
|
1 |
2 |
1 |
1 |
|
|
||||||
|
|
|
3 |
|
6 |
|
6 |
|
3 |
u1 |
|
|
|
k |
−6 |
|
3 |
−3 |
−6 |
u2 |
= RHS (Right Hand Side) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
2 |
|
1 |
u |
3 |
|
|
|
|
− |
6 |
− |
3 |
|
3 |
− |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
2 |
u |
4 |
|
|
|
|
− |
3 |
− |
6 |
− |
6 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(4.177)
(4.178)
Матрица жесткости симметрична. Обычно область, для которой ищется решение, состоит не из одного квадратного элемента, поэтому на следую• щем шаге надо получить матрицу жесткости для всей области. В качестве

Метод конечных элементов для решения уравнения в частных |
|
производных |
67 |
примера рассмотрим область, состоящую из четырех единичных квадрат• ных элементов и девяти узлов. Получим следующую глобальную матрицу жесткости A:
− |
6 |
3 |
|
1 3 |
|
−26 |
− 3 |
|
|
− 6 |
−1 |
6 |
|
|
− 1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
2 |
− 6 |
2 |
|
|
1 |
− |
6 |
|
|
|
1− 3 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||
− |
6 |
|
1− |
3 |
|
1 |
|
1 |
3 + 3 |
1 |
2 |
−2 |
6 |
−2 |
6 |
2 |
|
1 |
|
1 |
− |
6 |
|
1− |
3 |
|
1 |
|
1 |
||||
|
1 |
|
6 |
|
3 |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||
A = |
|
3 |
|
6 |
|
6 |
3 |
6 |
2 |
6 |
3 |
+ 3 |
|
|
3 |
+ |
3 |
|
6 |
|
6 |
|
3 |
|
6 |
1 |
|
6 |
|
3 |
|
||
|
|
|
|
|
+ 3 |
|
|
6 |
|
|
|
|
|||||||||||||||||||||
|
|
1 |
|
− 1 |
|
|
|
|
2 |
|
|
|
1− |
|
1 |
|
|
− |
|
|
1 |
|
|
|
|
|
|
|
|||||
− − −1 |
|
− 1 |
− − |
|
|
|
1 |
|
|
1 |
|
−2 |
|
−2 |
− − −1 |
|
− 1 |
||||||||||||||||
|
|
|
|
− |
3 |
|
|
− |
6 |
|
1 |
|
|
− |
6 |
−1 |
6 |
|
3 |
+ 3 |
2 |
|
|
− |
3 |
|
|
− |
6 |
|
|||
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
1− |
3 |
1 |
|
|
|
|
1 |
3 |
1 |
2 |
− |
6 |
2 |
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
− |
3 |
|
|
− |
6 |
−1 |
6 |
|
|
− |
3 |
− |
6 |
3 |
|
1 |
3 |
|
−2 |
6 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
− |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 3 |
|
|
|
− |
6 |
|
|
|
6 |
|
|
3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u1
u2
u3
u4
A · u5 |
= RHS |
(4.179) |
|
|
u6 |
|
|
u7 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
u8 u9
Рис. 22.
68 |
|
|
|
|
|
|
|
|
|
|
|
Детерминированное моделирование |
||||||||||
Выполнив необходимые арифметические действия, получим: |
|
|||||||||||||||||||||
|
2 |
|
|
1 |
−26 |
|
1 |
|
1 |
− |
1 |
|
|
|
|
|
|
|
|
|
|
|
−6 |
31 |
−3 |
−1 |
|
|
|
|
|
|
|
|
|||||||||||
|
31 |
−46 |
|
1 |
− |
6 |
− |
3 |
|
1 |
|
|
|
|
|
|
u1 |
|
|
|||
|
|
1 |
1 |
|
|
|
|
|
|
|
u2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
||||
|
1 |
−1 |
|
|
4 |
|
−1 |
− |
|
|
1 |
|
1 |
|
|
u |
4 |
|
||||
|
|
6 |
|
3 |
3 |
|
3 |
|
|
3 |
|
6 |
|
6 |
|
3 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
3 |
|
|
|
|
|
|
|
u3 |
|
|
|||
− |
1 |
− |
1 |
|
1 |
|
1 |
−8 |
|
|
1 |
− |
1 |
− |
1 |
|
1 |
u |
5 |
= RHS |
||
|
− |
3 |
− |
3 |
− |
3 |
− |
3 |
3 |
|
−4 |
3 |
− |
3 |
− |
3 |
− |
3 |
|
|
|
|
|
|
1 |
1 |
|
|
1 |
|
|
1 |
1 |
u |
6 |
|
|
||||||||
|
|
|
− |
3 |
− |
6 |
|
|
− |
3 |
3 |
|
|
|
− |
3 |
− |
6 |
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
2 |
|
1 |
|
u |
7 |
|
|
|||||
|
|
|
|
|
|
|
− |
6 |
− |
3 |
|
1 |
3 |
1 |
−4 |
6 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
u |
|
|
|
||||||
|
|
|
|
|
|
|
− |
3 |
− |
3 |
− |
3 |
− |
6 |
3 |
|
−2 |
6 |
|
8 |
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
1 |
|
u |
9 |
|
|
|||||
|
|
|
|
|
|
|
|
|
− |
3 |
− |
6 |
|
|
− |
6 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(4.180) Далее надо наложить граничные условия и решать алгебраическую си• стему. Наложение граничных условий уменьшает количество неизвестных и уравнений. В нашем примере будем считать, что задана температура на левой и правой границах пластины, а через верхний и нижний края нет потока тепла. Учитывая, что температура в узлах, лежащих на вертикаль• ных границах, известна, нам надо найти ее только в узлах 2, 5, 8. Правая часть в узлах 2 и 8 равна нулю, т. к. через них поток тепла равен нулю.
Напомним, что правая часть имеет вид:
Z |
∂nω d |
(4.181) |
|
∂u |
|
В узле 5 правая часть также равна нулю, т. к. это внутренний узел. Для получения решения надо решить три линейных уравнения.
4.4 Метод граничных элементов для решения уравнений в частных производных
Дельта-функция Дирака
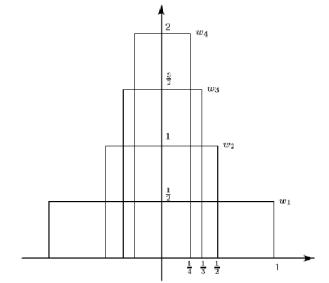
Прежде, чем познакомиться с методом граничных элементов, надо опре• делить фундаментальное решение. Фундаментальное решение тесно связа• но с дельта–функцией Дирака. Рассмотрим последовательность распреде• лений силы, приложенной к большой пластине
ωn (x) = ( |
n , |
x |
< 1 |
(4.182) |
0, |
|x| |
> 1 |
||
|
2 |
|
n |
|
|
|
| | |
n |
|
Метод граничных элементов для решения уравнений в частных
производных |
|
69 |
Каждое такое распределение удовлетворяет условию |
|
|
∞ |
|
|
Z |
ωn (x)dx = 1. |
(4.183) |
−∞
Суммарная сила, приложенная к пластине, равна 1. При увеличении n область, в которой сила отлична от нуля, уменьшается. Нестрого дельта• функцию можно определить следующим образом:
δ(x) = lim ωn (x), |
(4.184) |
n→∞ |
|
(см. рис. 23)
Рис. 23.
Свойства дельта-функции
∞
Z
δ(x)dx = 1, |
(4.185) |
−∞
70 |
Детерминированное моделирование |
|
∞ |
|
|
Z |
δ(x)h(x)dx = h(0). |
(4.186) |
−∞
Это можно показать следующим образом:
∞
R
δ(x)h(x)dx
−∞
= limn→∞
= limn→∞ |
∞ |
|
|
|
ωn (x)h(x)dx = |
|
|||
|
1 |
−∞ |
|
(4.187) |
|
n |
R |
|
|
n |
h(x)dx = lim n h(ξ) 2 |
= h(0). |
||
−Rn |
|
n→∞ 2 n |
|
|
2 |
1 |
|
|
|
|
|
|
|
|
Кроме приведенных выше, дельта-функция еще обладает следующими свойствами:
∞ |
|
|
|
|
|
|
|
Z |
δ(ξ − x)h(x)dx = h(ξ), |
(4.188) |
|||||
−∞ |
|
|
|
|
|
|
|
|
δ(ξ |
) = |
H |
0 |
(ξ |
) |
(4.189) |
|
|
− x |
|
|
− t |
|
|
Дельта-функция — производная функции Хэвисайда
0 ξ < t
H(ξ − t) = (4.190) 1 ξ > t
Двумерная дельта-функция вводится следующим образом
δ(ξ − x, η − y) = δ(ξ − x)δ(η − y) |
(4.191) |
Фундаментальное решение
Построим фундаментальное решение для двумерного уравнения Лапла• са. Это решение называется также функция Грина. Рассмотрим двумерное уравнение Лапласа [7]:
∂2u |
+ |
|
∂2u |
= 0 |
(4.192) |
|
∂x2 |
∂y2 |
|||||
|
|
|
||||
в области
Ω <2.
