Математическое моделирование / belova

t or n

FTCS

(a)x or j

Рис. 4.

Аналогично определяется

δy2unj,l .

Далее надо решить систему линейных уравнений. Система уже не яв• ляется трехдиагональной, как в одномерном случае, но является сильно разреженной. Ее можно решать, используя специальную технику примени• мую для разреженных матриц.

Существует другой способ обобщения одномерного метода Кранка–Ни- колсона на двумерную задачу. При этом также используется схема второ• го порядка точности по времени и пространству и безусловно стабильная, однако в этом случае получаются алгебраические уравнения, которые ре• шаются проще.

При этом каждый шаг по времени делится на два шага длиной t/2 и во время одного шага изменяется одна независимая переменная, например x, а во время другого — переменная y.

При этом на каждом шаге надо решать трехдиагональную систему.

Методы Фурье для решения граничных задач

Методы Фурье применимы лишь к уравнениям с постоянными коэффи• циентами. Кроме того, границы области моделирования должны совпадать с линиями координатной сетки.

Рассмотрим применение метода Фурье к решению уравнения вида:

Будем использовать следующую разностную схему:

Дискретное обратное преобразование Фурье для x и y имеет вид:

m=0 n=0

Правую часть уравнения также можно разложить в ряд Фурье:

m=0 n=0

Если мы подставим эти выражения в разностное уравнение, то получим:

Стратегия решения разностного уравнения методом Фурье состоит в следующем:

Методы конечных разностей для решения уравнений в частных

m=0 n=0

2.Вычисляем коэффициенты разложения umn из уравнения (4.98)

3.Вычисляем uij из обратного преобразования Фурье (4.96)

Изложенная выше процедура справедлива для периодических гранич• ных условий

Рассмотрим сначала граничные условия Дирихле u = 0 на прямоуголь• ной области, тогда разложение Фурье примет вид:

Вычислим коэффициенты Фурье правой части

При помощи обратного преобразования Фурье вычисляем решение. Если граничные условия неоднородны, то находится решение однород•

ного уравнения, удовлетворяющее граничным условиям. При этом гранич• ное условие также раскладывается в ряд Фурье, а затем решение уравне• ния с неоднородными граничными условиями представляется в виде суммы решений уравнения с однородными граничными условиями и решения од• нородного уравнения с неоднородными граничными условиями.

В случае граничных условий Неймана решение ищется в виде разложе• ния по косинусам:

После одного уровня CR–метода мы уменьшили число уравнений в два раза, т.к. результирующие уравнения имеют тот же вид, что исходные, мы можем повторить операцию. Если для простоты мы выберем число точек сетки равным степени двойки, то в конце концов получим:

Здесь u0 и uJ перенесены в правую часть, т.к. это известные значения искомой функции на границе. Полученное уравнение может быть решено при помощи стандартного трехдиагонального алгоритма. Два уравнения, которые надо было решить на предыдущем шаге (f − 1), содержали два неизвестных: uJ/4 и u3J/4. Уравнение для uJ/4 содержит u0 и uJ/2 уже из• вестные, и, следовательно, тоже может быть решено с использованием алгоритма для трехдиагональной матрицы. Таким образом, нам надо ре• шить J − 1 трехдиагональную систему. На практике уравнения несколько преобразовывают, чтобы избежать численных нестабильностей.

Комбинация метода Фурье и CR–метода, называемая методом FACR, также применяется для решения рассмотренных уравнений. На r–шаге CR–метода используют Фурье–разложение по y и получают трехдиаго• нальную систему в x–направлении для каждой y–Фурье моды.

4.3 Метод конечных элементов для решения уравнения в частных производных

Метод конечных элементов (МКЭ) — численный метод решения уравнений в частных производных, применяемый в первую очередь в при• кладной механике [4,7],широко используется для решения задач механики деформируемого твёрдого тела, теплоообмена, гидродинамики и электро• магнитных полей. С точки зрения вычислительной математики, идея мето• да конечных элементов заключается в том, что минимизация функционала вариационной задачи осуществляется на совокупности функций, каждая из которых определена на своей подобласти. С точки зрения численного ана• лиза системы МКЭ можно рассматривать как одну из конкретных ветвей диакоптики — общего метода исследования систем путём их расчленения. Возникновение метода конечных элементов связано с решением задач кос• мических исследований в 1950-е годы (идея МКЭ была разработана со• ветскими учёными ещё в 1936 году, но из-за неразвитости вычислительной техники метод не получил развитие). Этот метод возник из строительной

механики и теории упругости, а уже затем было получено его математиче• ское обоснование. Существенный толчок в своём развитии МКЭ получил в 1963 году после того, как было доказано то, что его можно рассматривать, как один из вариантов распространённого в строительной механике метода Рэлея–Ритца, который путём минимизации потенциальной энергии сводит задачу к системе линейных уравнений равновесия. После того, как была установлена связь МКЭ с процедурой минимизации, он стал применяться к задачам, описываемым уравнениями Лапласа или Пуассона. Область при• менения МКЭ значительно расширилась, когда было установлено (в 1968 году), что уравнения, определяющие элементы в задачах, могут быть легко получены с помощью вариантов метода взвешенных невязок, таких как ме• тод Галёркина или метод наименьших квадратов. Это сыграло важную роль в теоретическом обосновании МКЭ, так как позволило применять его при решении многих типов дифференциальных уравнений. Таким образом, ме• тод конечных элементов превратился в общий метод численного решения дифференциальных уравнений или систем дифференциальных уравнений.

С развитием вычислительных средств возможности метода постоянно расширяются, также расширяется и класс решаемых задач. Практически все современные расчёты на прочность проводят, используя метод конеч• ных элементов.

Метод конечных элементов (МКЭ) является проекционным методом, предназначенным для решения задач, для которых модель объекта зада• ется системой дифференциальных уравнений в частных производных с за• данными краевыми условиями [8].

Здесь L — дифференциальный оператор (например, оператор Лапла• са), V — фазовая переменная — неизвестная функция, которую следует найти, P — величина, не зависящая от V .

V( ) = V — граничное условие первого рода (Дирихле), то есть на границе задано значение фазовой переменной.

Будем искать решение с помощью функции, имеющей следующий вид:

m=1

Здесь V — приближенное решение, F — функция, удовлетворяющая граничным условиям, Nm — пробные функции, которые на границе обла• сти должны быть равны нулю, Am — неизвестные коэффициенты, которые необходимо отыскать из условия наилучшего удовлетворения дифференци• альному оператору, M — количество пробных функций. Если подставить

V в исходный дифференциальный оператор, то получим невязку, прини• мающую в различных точках области разное значение.

Необходимо сформулировать условие, позволяющее минимизировать эту невязку по всей области. Одним из вариантов такого условия может быть следующее уравнение:

Z

S

Здесь Wn — некоторые весовые функции, в зависимости от выбора которых различают варианты метода взвешенных невязок, S — область пространства, в которой ищется решение. При выборе дельта–функций в качестве весовых функций будем иметь метод, который получил назва• ние метод поточечной коллокации, для кусочно–постоянных функций

— метод коллокации по подобластям, но наиболее распространенным является метод Галеркина, в котором в качестве весовых функций вы• бираются пробные функции N. В этом случае, если количество пробных функций равно количеству весовых функций, после раскрытия определен• ных интегралов приходим к замкнутой системе алгебраических уравнений относительно коэффициентов A.

где коэффициенты матрицы K и вектора Q вычисляются по формулам:

ZZ

После нахождения коэффициентов A и их подстановки, получаем ре• шение исходной задачи. Недостатки метода взвешенных невязок очевидны: поскольку решение ищется сразу по всей области, то количество пробных и весовых функций должно быть значительным для обеспечения прием• лемой точности, но при этом возникают трудности при вычислении коэф• фициентов Kij и Qi, особенно при решении плоских и объемных задач, когда потребуется вычисление двойных и тройных интегралов по обла• стям с криволинейными границами. Поэтому на практике этот метод не использовался, пока не был изобретен метод конечных элементов (МКЭ). Идея метода взвешенных невязок заключается в следующем: можно вос• пользоваться простыми пробными и весовыми функциями, но не во всей

области S, а в ее отдельных подобластях (конечных элементах), обеспечи• вая точность решения задачи использованием большого числа конечных элементов (КЭ). При этом КЭ могут быть простой формы, и вычисление интегралов по ним не должно вызывать особых затруднений.

Математически переход от метода взвешенных невязок к МКЭ осу• ществляется с использованием специальных пробных функций, которые также называются глобальными базисными функциями, обладающими сле• дующими свойствами:

1.В узле аппроксимации функции имеют значение, равное единице

2.Функции отличны от нуля только в КЭ, содержащих этот узел ап• проксимации, во всей остальной области они равны нулю

Базисные функции конечных элементов

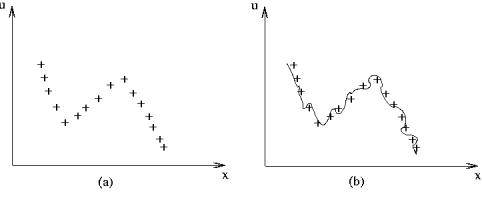
Пусть имеется полученное экспериментально одномерное распределе• ние температуры вдоль балки (x — координата точки, в которой измерена температура) (рис. 5, случай (a)), и мы хотим найти математическую функ• цию, описывающую это распределение.

Рис. 5.

Можно попытаться описать эту зависимость при помощи полинома и найти коэффициенты полинома при помощи метода наименьших квадратов. Полином высокой степени достаточно точно описывает набор эксперимен• тальных данных, но при этом возникают нежелательные осцилляции (см. рис. 5, случай (б)), полином же низкой степени, плохо описывает кривую.

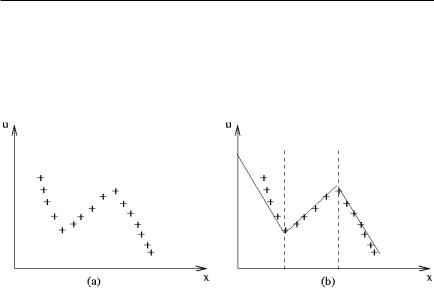
Попробуем решить задачу, разбив балку на области (элементы), и описать каждую область при помощи полинома невысокой степени. Введем пара• метр s, который характеризующий расстояние от точки до края балки, и при помощи метода наименьших квадратов найдем для каждого элемента (области) линейный полином, описывающий каждую область наилучшим образом (рис. 6).

Рис. 6.

Линейные базисные функции

Как видно из рисунка, линейные полиномы хорошо описывают тем• пературное поле в каждой области, но получившаяся аппроксимация не является непрерывной, на границах областей решения надо «сшивать».

Это можно сделать следующим образом. Пусть u1 и u2 — значения тем• пературы u в узлах, тогда линейную функцию между этими двумя узлами можно записать в виде

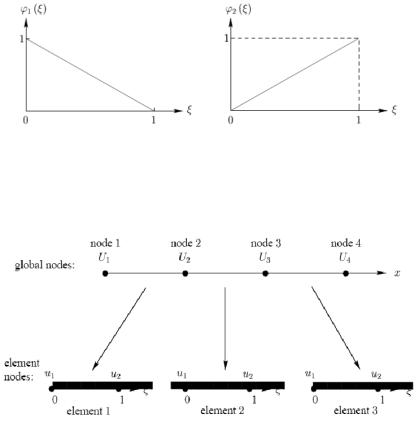
Линейные базисные функции имеют вид, указанный на рис. 7.

Рис. 7.

На рисунке 8 приведена связь между глобальными узлами и узлами элемента

Рис. 8.

Первый элемент интерполируется выражением

u(ξ) = ϕ1 (ξ)u1 + ϕ2 (ξ)u2