
ДискретнаяМатематика / Student Solutions Manual / chapter 6
.pdf
6.6 Exercises
1.Find a graph with 12 edges having six vertices of degree three and the remaining vertices of degree less than three.
1.
3 2
3
3
3
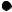 2
2
2
3
3
3.(a) Construct a graph with six vertices and degree sequence 1, 1, 2, 2, 3, 3.
(b)Construct a graph with six vertices and degree sequence 1, 1, 3, 3, 3,
3.
(c)Can you nd at least two graphs with each of these degree sequences? 3. (a)
3. (b)
3. (c)
1-1-2-2-3-3 1-1-3-3-3-3

5.Determine all possible degree sequences for graphs with ve vertices containing no isolated vertex and six edges.
5. 1, 2, 2, 3, 4; 2, 2, 2, 2, 4; 2, 2, 2, 3, 3; 1, 2, 3, 3, 3
7.Let d1; d2; : : : ; dn be a nondecreasing sequence of non-negative integers
Pn representing the degrees of the vertices of some graph. Prove that i=1 di
is even. Is the converse to this result true?
7.The rst question is answered by Theorem 3. The second question is answered in the negative by the sequence 2, 2.
9.For n = 2; 3; 4; 5, determine a relationship between the number of edges and the number of vertices in an n-regular graph with p vertices, where p = 1; 2; 3; : : :. Construct all 3-regular graphs on four and six vertices.
9.For n = 2: 2E = 2V or V = E. For n = 3: V = (2/3)E or V = 0
(mod 2) and E = 0 (mod 3). For n = 4: E = 2V . For n = 5: V = (2=5)E or E = 0 (mod 5) and V = 0 (mod 2).

11.Draw a graph with 16 vertices labeled with the elements of f0; 1g f0; 1g f0; 1g f0; 1g and edges that correspond to the edges in Q4.
11.
0000 |
0010 |
|
|
|
|
|
1000 |
1010 |
0100 |
0110 |
|
0001 |
0011 |
|
0101 |
1100 |
1110 |
|
1001 |
1011 |
|
0111 |
|
1101
1111
13. Prove that Qn is bipartite for n = 2; 3; 4; : : : :
13. Let n0 = 1: Let T = fn 2 N : Qn is bipartiteg.
(Base step) For n = 1, the result is clear since the two vertices form a bipartition with each set containing one of the vertices. Therefore, 1 2 T .
(Inductive step) Choose n such that n n0 and n 2 T : Prove n+1 2 T . All the vertices in Qn with leading vertex 0 form a Qn, which is bipartite by the inductive hypothesis. Similarly, the vertices with rst entry 1 form a Qn which is also bipartite by the inductive assumption. Let V1; V2 be a bipartition of the vertices with leading entry 0. Let V3; V4 be a bipartition of the vertices with leading entry 1. If 00 0 2 V1 and 100 0 2 V3, then V1 [ V4 and V2 [ V3 form a bipartition of
15.Construct C5; K3;3; and K2;4:
15.
K 5 |
K 3, 3 |
K 2, 4
17. For the graph
|
1 |
6 |
2 |
5 |
3 |
4
do the following:
(a)Find subgraphs without isolated vertices that are n regular for n = 2; 3; 4; 5:
(b)Find one path for each of the lengths three, four, ve, and six.
(c)Find one cycle of each of the sizes three, four, ve, and six.
(d)Find one trail for each of the lengths 6, 8, 10, and 12.
(e)Find the induced subgraphs determined by the sets of vertices: f1, 3, 4g, f2, 3, 5, 6g, f2, 4, 6g, and f1, 3, 4, 5, 6g.
The solutions for parts (a), (b), (c), and (e) should be drawings of graphs with the vertices labeled as in the gure. For part (d), list the vertices as they occur in the trail.

17. (a)
1 |
|
1 |
|
1 |
|
|
1 |
6 |
2 |
6 |
2 |
6 |
2 |
6 |
2 |
5 |
3 |
5 |
3 |
5 |
3 |
5 |
3 |
4 |
|
4 |
|
4 |
|
|
4 |
17. (b)
1 |
|
|
1 |
|
1 |
|
6 |
2 |
6 |
2 |
6 |
2 |
none exist for n = 6 |
5 |
3 |
5 |
3 |
5 |
3 |
|
4 |
|
|
4 |
|
4 |
|
17. (c)
|
1 |
|
1 |
1 |
|
|
1 |
6 |
2 |
6 |
2 |
6 |
2 |
6 |
2 |
5 |
3 |
5 |
3 |
5 |
3 |
5 |
3 |
|
4 |
|
4 |
4 |
|
|
4 |
|
|
|
|
1 |
|
|
1 |
17. (d)
|
4 |
|
4 |
|
|
1 |
|
1 |
|
|
|
|
start |
|
6 |
2 |
6 |
2 |
6 |
5 |
3 |
5 |
3 |
5 |
4 |
|
4 |
1 |
|
1 |
start |
|
start |
|
|
|
2 |
6 |
2 |
end |
end |
|
3 |
5 |
3 |
|
end |
|
|
|
end |
|
|
4 |
4 |
4 |
4 |
17. (e)
1 |
|
|
1 |
|
|
1 |
|
6 |
2 |
6 |
2 |
6 |
|
3 |
5 |
3 |
|
3 |
5 |
3 |
4 |
|
|
4 |
|
|
4 |
|
|
|
|
|
|
19.Show that 1; 2; 2; 3; 4 is graphical but that 1; 3; 3; 3 is not. Prove the theo-
rem of Havel-Hakimi that for n 1, the sequence d1; d2; : : : ; dn is graphical if and only if d1; d2; : : : ; dn dn dn dn+1 1; : : : ; dn 1 1 is graphical.
19. 1, 2, 2, 3, 4 is graphical if and only if 0, 1, 1, 2 is graphical if and only if 0, 0, 0 is graphical. Starting with three isolated vertices a graph can be built that has the required degree sequence. For 1, 3, 3, 3 you are lead to 0, 2, 2 which cannot be graphical.
Suppose d1; d2; : : : ; dn dn 1; dn dn 1; : : : ; dn 1 1 is graphical. This means that there is a graph G with n 1 vertices with d1; d2; : : : ; dn dn
1; dn dn 1; : : : ; dn 1 1 as its degree sequence. The vertices of G can be labeled v1; v2; v3; : : : ; vn 1 so,
di |
1 n dn i n 1 |
deg(vi) = di |
1 i n dn 1 |
A new graph H can be constructed by adding a new vertex vn to G and joining vn to the dn vertices where n dn i n 1. Then, deg(vi) = di: for every vertex vi of H. Therefore, the degree sequence is graphical.
Now, assume d1; d2; : : : ; dn is graphical. Therefore, there are one or more graphs with n vertices with this degree sequence. Among all these graphs,
let G be one of them such that V = fv1; v2; : : : ; vng where deg(vi) = di for 1 i n; and the sum of the degrees of the vertices adjacent to vn
is maximum. We claim that in G, the vertex vn must be adjacent to dn vertices having degrees dn dn ; : : : ; dn:
Suppose to the contrary, that vn is not adjacent to vertices having degrees dn dn ; : : : ; dn: Then there must exist two vertices vj and vk with dj > dk such that vn is adjacent to vk but not vj : Since deg(vj ) > deg(vk ); there must be some vertex vm such that vm is adjacent to vj , but not to vk : Removing the edges (vn; vk ) and (vj ; vm) and adding edges (v1; vj ) and (vk ; vm) produces a graph G1 that also has degree sequence as given. However, in G1 the sum of the degrees of the vertices adjacent to v1 is larger than that in G. This contradicts the property of G. If we remove the vertex vn from G and the edges incident to vn, we obtain a graph H whose degree sequence is d1; d2; : : : ; dn dn 1; dn dn 1; : : : ; dn 1 1:
21.Let G = (V; E) be a bipartite graph with vertex partition V = A [ B. Prove that if j A j 6= j B j; then G is not Hamiltonian.
21. The vertices on a path in G alternately belong to A and B. If x1; x2; : : : ; xn; x1 is a closed path that goes through each vertex once, then x1; x3; x5; : : : must belong to one of the sets, say A: Since (xn; x1) is an edge, n must be even and x2; x4; x6; : : : ; xn all belong to B: Therefore jAj = jBj:

23.Find a Hamiltonian cycle in the following graphs:
23. G1: 1 - 7 - 8 - 9 - 10 - 6 - 5 - 4 - 3 - 2 - 1
|
|
1 |
|
|
|
7 |
|
5 |
6 |
8 |
2 |
|
|
|
10 9
4 |
3 |
G1
|
|
1 |
|
|
|
7 |
|
10 |
|
14 |
2 |
|
|
|
|
|
|
|
9 |
|
11 |
|
3 |
6 |
8 |
|
|
|
|
|
|
|
|
||
|
13 |
12 |
|
|
|
|
|
|
|
||
|
5 |
G2 |
|
4 |
|
|
|
|
|
||
|
|
|
|
|
G2 : 1 - 2 - 14 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 13 - 12 - 11 - 10 - 1
25.Complete the proof of Example 5 in Section 6.3.1.
25. Suppose a Hamiltonian cycle in (a) contains the edges (1, 2) and (2, 4). Edges (2, 5) and (2, 3) can be removed since 2 is already incident to two edges. We then must complete a Hamiltonian cycle in
1 |
2 |
3 |
|||
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
6 |
5 |
4 |
|
|
which is clearly impossible.
Suppose a Hamiltonian cycle in (a) contains the edges (2, 5) and (2, 3). Edges (1, 2) and (2, 4) can be removed since 2 is already incident to two edges. We then must complete a Hamiltonian cycle in
1 |
2 |
3 |
||
|
|
|||
|
|
|
|
|
6 |
5 |
4 |
|
|
which is clearly impossible.

Suppose a Hamiltonian cycle in (a) contains the edges (2, 5) and (2, 4). Edges (1, 2) and (2, 3) can be removed since 2 is already incident to two edges. We then must complete a Hamiltonian cycle in
1 |
2 |
3 |
|
6 |
5 |
4 |
|
|
which is clearly impossible.
27.Show that the function F (a) = 3; F (b) = 1; F (c) = 4; and F (d) = 2 is an isomorphism between the graphs G and H as shown.
|
|
1 |
2 |
|
a |
b |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
3
d c
4
H
G
27. Clearly, F is a bijection between the vertex sets of the two graphs. It remains to show that edges are mapped to edges in a 1-1 and onto fashion.
F ((a; b)) = (3; 1)
F ((b; c)) = (1; 4)
F ((c; d)) = (4; 2)
F ((d; a)) = (2; 3)
F ((b; d)) = (2; 1)
It is clear that this is a bijection between the two edge sets.
29.Let G = (V; E) and H = (V1; E1) be isomorphic graphs. Prove the degrees of the vertices of G are exactly the degrees of the vertices of H. Show that j V j = j V1 j and j E j = j E1 j alone do not imply that G and H are isomorphic.
29. Since G and H are isomorphic, there exists an isomorphism : V (G1) ! V (G2): Let u be any vertex of G, and suppose deg(u) = n: Suppose further that the image of u in G2 is v. We prove that deg(v) = n:
Since deg(u) = n; the graph G contains vertices u1; u2; : : : ; un which are adjacent to u, while every other vertex of G is not adjacent to u. Let(ui) = vi for i = 1; 2; : : : ; n: Then v is adjacent to each of the vertices v1; v2; : : : ; vn; since is an isomorphism. Furthermore, these are the only vertices adjacent to v, since u is adjacent to x in G if and only if v is adjacent to (x) in H. Thus, deg(v) = n:

31. Prove that G and H as shown are not isomorphic:
4
a |
b |
5 |
3 |
f |
c |
|
6 |
|
|
1 |
2 e |
d |
G |
|
H |
31. The vertices of degree three span nonisomorphic subgraphs in the two graphs. Alternatively, the only vertices of degree two in the rst graph (3 and 4) are connected. The only vertices of degree 2 in the second graph (a and b) are not connected.
33. Prove that no pair of G1, G2, and G3 as shown are isomorphic:
G1 |
G 2 |
G 3 |
33. G1 and the other two graphs have nonisomorphic subgraphs spanned by the vertices of degree three. Therefore, G1 is not isomorphic to either G2 or G3. For G2 and G3 the vertices of degree two span nonisomorphic subgraphs so G2 is not isomorphic to G3.
35.For each graph shown in Exercise 16, construct both an adjacency matrix and an adjacency list representation.
Note. For all problems dealing with adjacency lists, assume that for each vertex the adjacencies are in increasing order.
35.
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
0 |
1 |
0 |
1 |
1 |
|
|
2 |
1 |
0 |
1 |
1 |
0 |
|
|
3 |
0 |
1 |
0 |
1 |
1 |
|
|
4 |
1 |
1 |
1 |
0 |
1 |
|
|
5 |
1 |
0 |
1 |
1 |
0 |
|
|
|
a |
b |
c |
d |
|
e |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
a |
0 |
1 |
1 |
0 |
1 |
|
|
b |
1 |
0 |
0 |
1 |
1 |
|
|
c |
1 |
0 |
0 |
1 |
0 |
|
|
d |
0 |
1 |
1 |
0 |
1 |
|
|
e |
1 |
1 |
0 |
1 |
0 |
|
|
|
u |
v |
w |
x |
|
|
|
|
|
|
|
||||
u |
0 |
0 |
0 |
1 |
|
|
|
v |
0 |
0 |
0 |
1 |
|
|
|
w |
0 |
0 |
0 |
1 |
|
|
|
x |
1 1 1 0 |
|
|
|
|||
Vertices |
|
|
List of |
|
|||
|
|
|
Adjacencies |
||||
1 |
|
|
2 |
5 |
4 |
|
|
2 |
|
|
1 |
3 |
4 |
|
|
3 |
|
|
2 |
5 |
4 |
|
|
4 |
|
|
1 |
2 |
3 |
5 |
|
51 3 4
Vertices |
|
List of |
|
|
Adjacencies |
||
|
|
|
|
a |
b |
c |
e |
b |
a |
e |
d |
c |
a |
d |
|
d |
c |
b |
e |
ea b d
Vertices |
List of |
|
Adjacencies |
ux
vx
wx
x |
u |
w |
v |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
37. Prove that if G = (V; E) is isomorphic to G, then j V j 0, 1 (mod 4). |
|
|||||||||
|
Let q = jEj |
|
|
|
|
|
|
|
|
|
37. |
and |
|
= jEj. q = |
|
, therefore 2q = p(p 1)=2 |
or |
||||
q |
q |
|||||||||
q = p(p 1)=4. |
Since q is an integer, p must either be of the form 4k or |
|||||||||
4k + 1 for some positive integer k.
