
ДискретнаяМатематика / Student Solutions Manual / chapter 1
.pdf1.2 Exercises
1.Let X be the set of all students at a university. Let A be the set of students who are rst-year students, B the set of students who are second-year students, C the set of students who are in a discrete mathematics course, D the set of students who are international relations majors, E the set of students who went to a concert on Monday night, and F the set of students who studied until 2 A.M. on Tuesday. Express in set theoretic notation the following sets of students:
(a)All second-year students in the discrete mathematics course.
Sample Solution. fx 2 X : x 2 B and x 2 Cg:
(b)All rst-year students who studied until 2 AM on Tuesday.
(c)All students who are international relations majors and went to the concert on Monday night.
(d)All students who studied until 2 AM on Tuesday, are second-year students, and are not international relations majors.
(e)All rstand second-year students who did not go to the concert on Monday night but are international relations majors.
(f)All students who are rst-year international relations majors or who studied until 2 AM on Tuesday.
(g)All students who are rstor second-year students who went to a concert on Monday night.
(h)All rst-year students who are international relations majors or went to a concert on Monday night.
1. (a) fx : x 2 X and x 2 B and x 2 Cg
1. (b) fx : x 2 X and x 2 A and x 2 F g
1. (c) fx : x 2 X and x 2 D and x 2 Eg
1. (d) fx : x 2 X and x 2 F and x 2 B and x 62Dg
1. (e) fx : x 2 X and (x 2 A or x 2 B) and x 62E and x 2 Dg
1. (f) fx 2 X : (x 2 A and x 2 D) or x 2 F g
1. (g) fx 2 X : (x 2 A or x 2 B) and x 2 Eg
1.(h) fx 2 X : x 2 A and (x 2 D or x 2 E)g
3.Write three descriptions of the elements of the set f2, 5, 8, 11, 14g.
3.f2; 5; 8; 11; 14g; fn 2 N : n = 3k 1 for some k 2 N such that 1 k 5g; or fn 2 Z; n = 3k + 2 for some k 2 Z such that 1 < k < 5g.
5.Which of the following pairs of sets are equal? For each pair that is unequal, nd an element that is in one but is not in the other.
(a)f0, 1, 2g and f0, 0, 1, 2, 2, 1g
(b)f0, 1, 3, f1, 2gg and f0, 1, 2, f2, 3gg
(c)ff1, 3, 5g, f2, 4, 6g, f5, 5, 1, 3gg and ff3, 5, 1g, f6, 4, 4, 4, 2g, f2, 4, 4, 2, 6gg
(d)ff5, 3, 5, 1, 5g, f2, 4, 6g, f5, 1, 3, 3gg and ff1, 3, 5, 1g, f6, 4, 2g, f6, 6, 4, 4, 6gg
(e); and fx 2 N : x > 1 and x2 = xg
(f); and f;g
5. (a) equal
5. (b) not equal; 3 is an element of the rst but not the second; 2 is an element of the second but not the rst.
5. |
(c) equal |
5. |
(d) not equal; f6,4g is an element of the second but not the rst. |
5. |
(e) equal |
5. |
(f) not equal; ; is an element of the second but not the rst. |
7. Let A = fn : n 2 N and n = 2k + 1 for some k 2 Ng; B = fn : n 2
Nand n = 4k +1 for some k 2 Ng; and C = fm 2 N : m = 2k 1 and k 2
Nand k 1g: Prove the following:
(a)35 2 A
(b)35 2 C
(c)35 62B
(d)A = C
(e)B A
(f)B C
(g)B A
(h)B C
7.(a) Solve 35 = 2k + 1 and verify k 0.
7.(b) Solve 35 = 2k 1 and verify k 1.
7.(c) Show that there is no solution for 35 = 4k + 1 with k 2 N.
7. (d) ( ) Let 2k0 + 1 2 A for some k0 2 N. Then 2k0 + 1 = 2(k0 + 1) 1. Since k0 2 N, we have k0 + 1 2 N f0g. Therefore, A C.
( ) Let 2k0 1 2 C for some k0 2 N f0g. Then 2k0 1 = 2(k0 1) + 1. Since k0 2 N f0g, we have k0 1 2 N. Therefore, C A.
Since A C and C A, we have proven that A = C.
7. (e) Let 4k0 + 1 2 B for some k0 2 N: 4k0 + 1 = 2(2k0) + 1. Since k0 2 N, we have 2k0 2 N: Therefore, B A.
7. (f) Let 4k0 + 1 2 B for some k0 2 N. 4k0 + 1 = 2(2k0 + 1) 1. Since k0 2 N, we have 2k0 + 1 2 N f0g. Therefore, B C.
7. (g) Use (e), (c), and (a).
7. (h) Use (f), (c), and (b).
9.Describe in words the di erence between ; and f;g.
9. The set ; has no elements. The set f;g is a one-element set { its element is ;.
1.4 Exercises
1.Let A = f1; 2; 3; : : : ; 10g; B = f2; 3; 6; 8g; and C = f3; 5; 4; 8; 2g: Find the following:
(a)B [ C
(b)B \ C
(c)B C
(d)A B
(e)A C
1. (a) f2, 3, 4, 5, 6, 8g
1. (b) f2, 3, 8g
1. (c) f6g
1. (d) f1, 4, 5, 7, 9, 10g
1.(e) f1, 6, 7, 9, 10g
3.Let A = f0; 3g and B = fx; y; zg: Find the following:
(a)A B
(b)A A B
(c)B A
(d)B A B
3. (a) f(0; x); (0; y); (0; z); (3; x); (3; y); (3; z)g
3.(b) f(0; 0; x); (0; 0; y); (0; 0; z); (0; 3; x); (0; 3; y); (0; 3; z); (3; 0; x); (3; 0; y); (3; 0; z); (3; 3; x); (3; 3; y); (3; 3; z)g
3.(c) f(x; 0); (x; 3); (y; 0); (y; 3); (z; 0); (z; 3)g
3.(d) f(x; 0; x); (x; 3; x); (y; 0; x); (y; 3; x); (z; 0; x); (z; 3; x); (x; 0; y); (x; 3; y); (y; 0; y); (y; 3; y); (z; 0; y); (z; 3; y); (x; 0; z); (x; 3; z); (y; 0; z); (y; 3; z); (z; 0; z); (z; 3; z)g
5.Prove Theorem 1(d).
5. We must prove (i) A [ (B [ C) (A [ B) [ C and (ii) (A [ B) [ C A [ (B [ C):
(i) Let x 2 A [ (B [ C): Then either x 2 A or x 2 B [ C: In the rst case x 2 A [ B (Theorem 1 (b)). Therefore, x 2 (A [ B) [ C by Theorem 1(b). In the second case, either x 2 B or x 2 C: When x 2 B, we have x 2 A [ B by Theorem 1 (b). Again by Theorem 1(b), x 2 (A [ B) [ C: When x 2 C; x 2 (A [ B) [ C by Theorem 1 (b). In any case, whenever x 2 A [ (B [ C); it follows that x 2 (A [ B) [ C:
Part (ii) is analogous and is left to the reader.
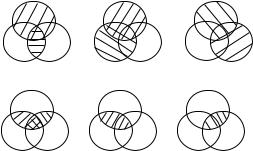
7.(a) Draw Venn diagrams to illustrate Theorems 3(a) and 3(b).
(b)Prove Theorem 3(a).
(c)Prove Theorem 3(b).
7. (a)
A
B
A U (B
A
U
A |
|
|
A |
= |
|
U |
|
|
|
|
|
C |
C |
|
|
B |
B |
C |
|
|
|
|
|
C) |
A U B |
|
A U C |
|
|
||
A |
|
|
A |
= |
U |
|
|
|
|
|
B C B C B C
A
U
(B U C)
A U B |
A U C |
7. (b) ( ) Show that
Suppose x 2 A\(B [C). It is necessary to show that x 2 (A\B)[(A\C).
A \ (B [ C) (A \ B) [ (A \ C)
Since x 2 A \ (B [ C), x 2 A and x 2 B [ C. From x 2 B [ C it follows that x 2 B or x 2 C.
Case I, x 2 B. Then, since x 2 A and x 2 B, x 2 A \ B. By Theorem 2 (b),
A \ B (A \ B) [ (A \ C):
Hence, x 2 (A \ B) [ (A \ C).
Case II, x 2 B. The proof that x 2 (A \ B) [ (A \ C) is analogous to
Case I.
( ) Show that
(A \ B) [ (A \ C) A \ (B [ C)
So, suppose x 2 (A \ B) [ (A \ C). It is necessary to show that x 2
A \ (B [ C).
Since x 2 (A \ B) [ (A \ C), x 2 (A \ B) or x 2 (A \ C).
Case I, x 2 (A \ B). Then x 2 A and x 2 B. Since x 2 B and B B [ C (Theorem 2(b)), x 2 B [ C. Hence x 2 A \ (B [ C).
Case II, x 2 (A \ C). Analogous to Case I.
7.(c) Analogous to (b).
9.Find three sets A, B, and C where A B [ C but A 6 B and A 6 C. 9. A = f2, 3, 4g. B = f1, 2, 3g. C = f3, 4, 5g.

11. Prove Theorem 7(c).
11. ()) Let A = B. If x 2 A, then x 62A: Since A = B, we conclude that x 62B: The proof in the other direction is analogous.
(() Let A = B: If x 2 A, then x 62A: But A = B so x 62B: But x 62B implies x 2 B: Therefore, A B: The proof in the other direction is analogous.
13. Let A = f1; 2; ff1; 2ggg:
(a) How many elements does A have? How many elements does P(A) have? How many elements does P(P(A)) have?
In parts (b)-(m) determine, whether each of the following is true, and if not, explain why not.
(b) 1 2 A (c) f1; 2g 2 A (d) ff1; 2gg 2 A (e) ; 2 A (f) 1 2 P(A) (g) f1; 2g 2 P(A) (h) ff1; 2gg 2 P(A) (i) ; 2 P(A) (j) 1 2 P(P(A)) (k) f1; 2g 2 P(P(A)) (l) ff1; 2gg 2 P(P(A)) (m) ; 2 P(P(A))
13. (a) 3, 8, 256
13. (b) T
13. (c) ff1; 2gg 2 A not f1, 2g
13. (d) ; A but ; 62A
13. (e) f1g 2 P(A) not 1
13. (f) T
13. (g) see (f)
13. (h) T
13. (i) T
13. (j) 1 2 A; f1g 2 P(A) and ff1gg 2 P(P(A))
13. (k) ff1; 2gg 2 P(P(A))
13. (l) T
13.(m) T
15.Which of the following statements are correct? Prove each correct statement. Disprove each incorrect statement by nding a counterexample.
(a) A and B are disjoint if and only if B and A are disjoint. (Read the statement carefully { the order in which the sets are listed might matter!)
(b) A [ B and C are disjoint if and only if both the following are true: (i) A and C are disjoint and (ii) B and C are disjoint.
(c) A \ B and C are disjoint if and only if both the following are true: (i) A and C are disjoint and (ii) B and C are disjoint.
(d) A [ B and C are disjoint if and only if one of the following is true: (i) A and C are disjoint or (ii) B and C are disjoint.
(e) A \ B and C are disjoint if and only if one of the following is true: (i) A and C are disjoint or (ii) B and C are disjoint.
(f) Let U be a universal set with A; B U: A and B are disjoint if and only if A and B are disjoint.

15. |
(a) True because intersection is commutative. |
15. |
(b) Since (A [ B) \ C = (A \ C) [ (B \ C); the conclusion follows. |
15. |
(c) A = f1; 2g; B = f3; 4g; C = f1; 3g |
15. |
(d) A = f1; 2g; B = f2; 3; 4g; C = f4g |
15. |
(e) (A \B) \C) = ;, but A \C = f1g and B \C = f3g are not empty. |
15.(f) U = f1; 2; 3gA = f1g; B = f2g
17.Given any four integers x1; x2; x3; and x4, none of which is even and none of which is a multiple of 5, prove that some consecutive product of these integers ends in the digit 1. A consecutive product is one term, two terms in a row, three terms in a row, or all four terms using the order in which the integers appear in the list x1; x2; x3; x4. (Hint. Use a proof by cases.)
17. We do a proof by contradiction. Suppose the statement is false. Then if any of the integers ends in the digit 1, the consecutive product consisting of just that one integer ends in the digit 1, as required. So from now on, suppose none of the integers ends in the digit 1.
Suppose an integer ends in the digit 3. Then no integer ends in the digit 7, because 3 7 ends in the digit 1. Thus each of the other integers ends in the digit 3 or 9. It is not possible that each of the four integers ends in the digit 3. It is also not possible that three integers end in the digit 3, since the remaining integer would have to end in 9, and 3 3 9 ends in 1. If two integers end in 3, then the remaining two must end in 9, which is not possible. If exactly one integer ends in 3, then the others must end in 9, which is not possible. Therefore, no integer ends in 3.
Now we know that each integer ends in 7 or 9. Suppose that an integer ends in 9. Then the others must end in 7, but this is impossible because 7 7 9 ends in 1. Thus all integers must end in 7, but this also is not possible.
Thus assuming that no consecutive product ends in 1 has lead to an impossible situation in every case. Therefore, the statement is true.
19. Prove by contradiction that |
p |
|
|
is not a rational number. |
|||||||
2 |
|||||||||||
|
p |
|
is a rational number. Without loss of |
||||||||
19. Suppose it is true that |
2 |
||||||||||
generality, we can assume there are integers m and n without common |
|||||||||||
factors such that |
|
|
|
p |
|
|
|
m |
|
||
|
|
|
|
2 |
= |
: |
|||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
n |
||
Then |
|
|
|
|
|
|
|
m2 |
|||
|
|
|
|
2 = |
|||||||
|
|
|
|
|
: |
||||||
|
|
|
|
n2 |
|||||||
Since m and n have no common factors, 2 must divide m. Therefore, m = 2 j for some integer j. This tells us that 2n2 = 4j2 and we can now
conclude that 2 divides n. Therefore, m and n have a common factor, p
which is a contradiction. We conclude that assumingpthat 2 is a rational number leads to a contradiction. Consequently, 2 is not a rational number.
21. Complete the proof of Example 12.
21. x _ y = y _ x: The operation x _ y is to nd the maximum of these two elements. The operation y _ x asks to nd the maximum of the same two elements. Therefore, x _ y = y _ x:
x _ (x ^ y) = x: The operation x ^ y nds the minimum of x and y. If the answer is x, you then nd x _ x which is x. If the answer is y, then x is less than y and the minimum of x and y is x.
x ^ (y ^ z) = (x ^ y) ^ z): The minfx, minfy; zgg is either x or minfy; zg. If x, then
minfminfx; yg; zg = x
as x y and x z: If minfy; zg is the minimum, then minfminfx; yg; zg = minfy; zg as y x.
x _(y _z) = (x _y) _z: maxfx, maxfy; zgg is either x or maxfy; zg. If x, then maxfmaxfx; yg; zg = maxfx; zg = x. If maxfy; zg is the maximum, then maxfmaxfx; yg; zg = maxfy; zg.
x_(x^y) = x: the minimum is minfx, maxfx; ygg is either x or maxfx; yg. If x, then the result holds. If maxfx; yg, then we still get x as x must be greater than y so maxfx; yg = x.
23.Let U be any set and let X = P(U ): Prove that X with the operations [ for meet and \ for join is a complemented lattice.
23. Use Example 13 with the interpretation of meet and join interchanged. For > use ; and for ? use X.
25.Prove that in a boolean algebra
a _ (b ^ c) = (a _ b) ^ c
if and only if
a _ (b ^ (a _ c)) = (a _ b) ^ (a _ c)
and
a ^ (b _ (a ^ c)) = (a ^ b) _ (a ^ c) This property of a boolean algebra is called modularity. 25. (()
(a _ b) ^ (a _ c) = ((a _ b) ^ a) _ ((a _ b) ^ c)
=(a _ (b ^ a)) _ (a _ (b ^ c))
=a _ ((b ^ a) _ (b ^ c))
=a _ (b ^ (a _ c))
The proof of
a ^ (b _ (a ^ c)) = (a ^ b) _ (a ^ c) follows by substituting ^ for _.
())
(a _ b) ^ c = (a ^ c) _ (b ^ c)
=c ^ (a _ (c ^ b))
=c ^ (a _ c) ^ (a _ b)
=(c ^ (a _ c)) ^ (a _ b)
=c _ (a ^ b)
27.Let U = f1, 2, 3, 4, 5, 6, 7, 8, 9, 10g be a universal set. Let A; B; C U such that A = f1, 3, 4, 8g, B = f2, 3, 4, 5, 9, 10g, and C = f3, 5, 7, 9, 10g. Use bit representations for A, B, and C together with U N ION; IN T ER; DIF F , and COM P to nd the bit representation for the following:
(a)A [ B
(b)A \ B \ C
(c)(A [ C) \ B
(d)(A B) [ C
(e)A \ (B (C \ B))
(f)A (B C)
(g)(A [ B) [ (C B)
27.(a) 1111100111
27. (b) 0010000000
27. (c) 0011100011
27. (d) 1010101111
27. (e) 0001000000
27. (f) 1010000100
27.(g) 1111101111
1.6Exercises
1.In a class of 35 students who are either biology majors or have blonde hair, there are 27 biology majors and 21 blondes. How many biology majors must be blonde?
1. Let A = fstudents who are biology majorsg. B = fstudents who are blondesg.
j A [ B j = j A j + j B j j A \ B j
35 = 27 + 21 j fbiology majors who are blondeg j j fbiology majors who are blondeg j = 13

3.A tennis camp has 39 players. There are 25 left handed players and 22 players have a two-handed back stroke. How many left-handed players have a two-handed back stroke if every player is represented in these two counts?
3. Let A = fleft handed playersg and B = fplayers with a two-handed back strokeg.
j A [ B j |
= j A j + j B j j A \ B j |
|
39 |
= |
25 + 22 j A \ B j |
jA \ Bj |
= |
25 + 22 39 |
=8
5.A marketing class did a survey of the number of fast food outlets near campus. The results of the survey showed the following:
|
Type of Food Sold |
No. of Outlets |
|
|
|
|
|
|
|
|
|
|
Hamburgers |
15 |
|
|
|
|
|
|
Tacos |
25 |
|
|
Pizza |
21 |
|
|
|
|
|
|
Hamburgers and tacos |
11 |
|
|
Hamburgers and pizza |
10 |
|
|
|
|
|
|
Tacos and pizza |
14 |
|
|
Hamburgers and tacos and pizza |
9 |
|
|
|
|
|
|
Served none of these items |
5 |
|
|
|
|
|
How many fast food outlets are there near campus?
5. Let A = fOutlets serving hamburgersg; B = fOutlets serving tacosg; and C = fOutlets serving pizzag. We will nd j A [ B [ C j and then add 5 since there are ve restaurants that do not t in any of these categories.
j A [ B [ C j = j A j + j B j + j C j j A \ B j j A \ C jj B \ C j + j A \ B \ C j
=15 + 25 + 21 11 10 14 + 9
=35
The nal answer is 40.

7.A marketing class did a sample survey to nd out how many of a class of 125 people owned CD's of the Beatles, Alabama, or Bob Marley. The results of the survey showed the following:
|
Recording Artist |
No. of Students Owning CD's |
|
|
|
|
|
|
Beatles |
65 |
|
|
|
|
|
|
Alabama |
46 |
|
|
|
|
|
|
Bob Marley |
29 |
|
|
Beatles & Alabama |
18 |
|
|
|
|
|
|
Beatles & Bob Marley |
21 |
|
|
Bob Marley & Alabama |
12 |
|
|
|
|
|
|
Beatles, Bob Marley, & Alabama |
9 |
|
|
|
|
|
How many of the students owned no CD featuring these performers?
7. Let A = fStudents who owned CD's featuring the Beatlesg; B = fStudents who owned CD's featuring Alabamag; and C = fStudents who
owned CD's featuring Bob Marleyg. We will rst nd j A [ B [ C j:
j A [ B [ C j = j A j + j B j + j C j
j A \ B j j A \ C j j B \ C j
+j A \ B \ C j
=65 + 46 + 29 18 21 12 + 9
=98
The answer we want is:
jA [ B [ Cj = Total no. of Students jA [ B [ Cj
=125 98
=27
9.How many integers between 1 and 250 are divisible by 3 or 5?
9.Let D3 = fIntegers in this range divisible by 3g; D5 = fIntegers in this range divisible by 5g; and D15 = fIntegers in this range divisible by 15g.
j D3 j = 83: j D5 j = 50: j D3 \ D5 j = j D15 j = 16: The answer we want is the number of distinct integers in this range that are divisible by either 3 or 5.
j D3 [ D5 j = j D3 j + j D5 j j D15 j = 117
