ДискретнаяМатематика / Student Solutions Manual / chapter 6

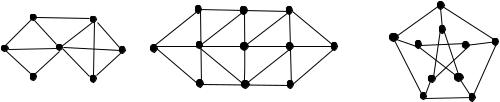
11.Prove that a graph G is connected if and only if G contains a spanning tree.

11. Consider a connected subgraph G0 of G that uses all the vertices of G and has as few edges as possible. G0 is acyclic and is a spanning tree else G0 has a cycle and the cycle involves some edge of G0. By Lemma 1 the graph G0 feg would be a connected subgraph with fewer edges. This contradiction shows that G0 is acyclic.

Lemma 1. Let G be a connected graph and (u; v) = e 2 C where C is a cycle, then G e is connected.

Proof. Let the cycle be x1 = u; x2 = v; : : : xn 1; xn = u. Let x; y be any vertices in G. There exists a trail trail from x to y: If u and v occur as consecutive vertices in the trail, replace uv by xnxn 1 : : : x2: This process gives a trail with one fewer occurrences of (u; v): Repeat until (u; v) is eliminated from any trail that is used to show that G is connected. Therefore, G e is connected.

13.For the following graphs:

(a)Find a MCST in each of the graphs G1, G2, and G3.

(b)Repeat part (a) for graph G1 if it must include (3, 5) and (1, 7) in the MCST.

(c)Repeat part (a) for graph G2 if it must include (3, 10), (6, 11), and (8, 9) in the MCST.

(d)Repeat part (a) for graph G3 if it must include (2, 9), (6, 8), and (4, 5) in the MCST.

13. (a) (i) (1, 2, 2), (6, 7, 2), (3, 5, 4), (4, 5, 2), (4, 6, 3), (7, 1, 3)

(ii)(1, 8, 3), (1, 2, 4), (2, 3, 3), (3, 10, 2), (3, 9, 2), (4, 11, 2), (4, 10, 2), (5, 6, 4)

(iii)(1, 2, 2), (1, 5, 3), (2, 3, 4), (2, 9, 3), (3, 8, 2), (4, 5, 3), (5, 6, 3), (7, 10, 4), (8, 10, 3), (7, 10, 1), (3, 6, 3)

13. (b) (1, 2, 2), (1, 7, 3), (6, 7, 2), (5, 6, 3), (3, 5, 4), (4, 5, 2)

13. (c) (1, 8, 3), (2, 3, 3), (3, 10, 2), (3, 9, 2), (4, 11, 2),( 4, 10, 2), (5, 6, 4), (6, 11, 3), (7, 10, 1), (8, 9, 4)

13. (d) (1, 2, 2), (2, 9, 3), (3, 8, 2), (4, 5, 3), (1, 5, 3), (5, 6, 3), (6, 8, 5), (8, 10, 3), (7, 10, 4)

15.A university has eight buildings that need to be connected so that each of the building's computer network is accessible to the networks in the other buildings. The distance between buildings is given in units of 1000 yards. The distances between buildings are given in the table that follows. These distance from building i to building j is the same as the distance from building j to building i.

Which pairs of buildings should be directly connected to connect all the buildings with a minimum total network length? What is the length of a minimum network? What are the di erent possible minimal networks?

15. (1, 4, 0.5), (7, 8, 0.5), (4, 5, 0.7), (6, 7, 0.6), (4, 8, 0.5), (3, 8, 1.0), (2, 3, 0.9) forms a MCST. The length of a minimum network is 4700 yards. The MCST is unique.

17.Find an algorithm for determining an MCST that is based on removing the maximum cost edge from a cycle at each step.

17.

CLASSICAL ALGORITHM:

Sort edges in order of decreasing cost. (Right now my image is that there are no duplicate costs; I suspect that won't cause any problems.)

For each edge (starting with most expensive) If the edge is part of a cycle then delete the edge from the graph.

ALTERNATE ALGORITHM:

While the graph has cycles pick a cycle, C. Find most expensive edge, E, in C. Delete E from graph.

Order edges in order of decreasing costs: e1; e2; :::; en:

Prove by induction on i that if ei 62M CST; then ei is deleted by the ALTERNATE ALGORITHM.

e1: trivial: If ei is in a cycle at all, then pick such a cycle, C. The rst time the alternate algorithm looks at C, it deletes e1. On the other hand, if e1 is not in any cycle, then neither algorithm deletes e1.

21.Write algorithm for the postorder traversal of any rooted tree. 21.

procedure P OST ORDER(node)

P OST ORDER(left child of node)

P OST ORDER(right child of node) list node

23.Draw a minimal depth decision tree that represents sorting four elements from a linearly ordered set. Only ve levels are required.

23.

a b c d

a : b

a c d

b

c : d

a d

b c

a : d

The branches of the decision tree can be constructed by interchanging letters in the branch shown.

25.A binary tree is said to be complete if all its leaves occur at the lowest level. For a complete binary tree of height h, determine the number of vertices at level i where 1 i h: Prove that the number of leaves is one more than the number of internal vertices.

1. (a) (D1) indeg(1) = 0; indeg(2) = 4; indeg(3) = 1; indeg(4) = 2; indeg(5) = 2; indeg(6) = 2

(D2) indeg(a) = 1; indeg(b) = 2; indeg(c) = 1; indeg(d) = 2; indeg(e) = 2; indeg(f) = 2

(D3) indeg(u) = 2; indeg(v) = 1; indeg(w) = 1; indeg(x) = 2; indeg(y) = 0

1. (b) (D1) outdeg(1) = 3; outdeg(2) = 0; outdeg(3) = 2; outdeg(4) = 3; outdeg(5) = 2; outdeg(6) = 1

(D2) outdeg(a) = 2; outdeg(b) = 1; outdeg(c) = 2; outdeg(d) = 2; outdeg(e) = 2; outdeg(f) = 1

(D3) outdeg(u) = 0; outdeg(v) = 2; outdeg(w) = 1; outdeg(x) = 1; outdeg(y) = 2

1. (c) (D1) none exists; (D2) c, f, d, e, a; (D3) none exists

1. (d) (D1) 1, 5, 3, 4, 6; (D2) d, b, e, f, d; (D3) none exists

1.(e) (D1) none exist; (D2) e, a, c, f, d, b, e; (D3) none exists

3.Prove that any directed acyclic graph contains at least one vertex with indegree of zero. Use this result to devise a di erent algorithm to do a topological sort.

3.Suppose not. Then pick a vertex x: Since indeg(x) 6= 0 there is a y1 such that (y1; x) is in the graph. Since indeg(y1) 6= 0 there is a y2 such that (y2; y1) is in the graph. Since G is acyclic, y2 6= x: Proceed in this way to construct an in nite directed path. Since the graph is nite, this is a contradiction.

For a topological sort, nd a vertex of indegree zero, list it, and then delete its edges from the graph. The resulting graph is still acyclic and so a new vertex of indegree zero can be found. List this vertex second, delete its edges from the graph. Proceed in this way until all the vertices have been listed.

5.Verify that the following graph D is a dag. Perform a topological sort on the vertices of the graph.

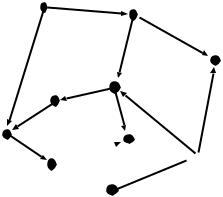
a

b

c

d f

e

D

5. Clearly, a is not in a directed cycle. Also j, e, and c are also not in a directed cycle. Now, since a is not in a directed cycle, b is not in a directed cycle. All that is left is a directed path d-i-h-g-f that cannot be extended. Therefore, since there are no directed cycles, D is a dag.

A topological sort: a-b-e-d-c-i-h-g-f-j

7.Prove that if a graph G contains an Eulerian circuit, then G is orientable.

7.For an Eulerian path, direct the edges in the direction of the path as you traverse the Eulerian circuit.

9.Prove that a connected undirected graph is orientable if and only if each edge is contained in a cycle.

9.Necessity clear. Su ciency: Choose any circuit C and orient its edges cyclically. If every edge of G is contained in C, proof complete. If not, choose any edge e which is not in C but which is adjacent to an edge of C. By hypothesis, e is contained in a circuit C0 whose edges we may direct cyclically (with the exception of those already directed). Proceed at each stage directing at least one new edge. At each stage G is strongly connected, so at the end it is.

11.Prove that if a directed graph is Eulerian, then it is strongly connected.

11. List the edges of an Eulerian circuit C. Pick any two vertices, x and y: Find an occurrence of x in C and an occurrence of y in C: Then,

C = A1xA2yA3

Now the directed trail xA2y can be re ned to become a directed path from x to y. Similarly, yA3A1x can be re ned to become a directed path form y to x:

13.Find a directed graph that is not Eulerian but for which the underlying graph is Eulerian.

13. (1, 2), (3, 2), (3, 4), (1, 4)

15.Challenge: A complete directed graph is a directed graph whose underlying graph is a complete graph. Show that the sum of the squares of the indegrees over all vertices is equal to the sum of the squares of the outdegrees over all vertices in any directed complete graph.

15.Start with a complete graph G on n nodes. Since G is complete, there

are

(a)n 1 edges incident with every node, and

(b)n(n 1)=2 edges (in all).

Form a directed graph by giving an orientation to each edge.

For each vertex, let indeg(v) be the indegree of v and outdeg(v) be the outdegree. So for each node v, since there are n 1 edges incident with it,

X

= n(n 1)2 n(n 1)2 + outdeg(v)2

v

X

=outdeg(v)2

v

De nition. A tournament Tn is a directed graph on n vertices such that each pair of vertices v; w is joined by one and only one of the directed edges (v; w) and (w; v): The score of a vertex of a tournament is its outdegree. The score sequence, or ranking, of a tournament is the sequence formed by arranging the scores of its vertices in non-decreasing order. A tournament is transitive if the existence of edges (a; b) and (b; c) imply the existence of the edge (a; c): The complement of a tournament is formed by reversing all the directions on each of the edges of a tournament.

17.Let D = (V; E) be a tournament. Prove that if a has maximum score, then for any vertex y, either there is an edge (a; y) or a vertex w and edges (a; w) and (w; y):

17. Let D = (V; E) be a tournament. Let a be the vertex of maximum

score. If there is an edge (a; y) for every y 2 D(G) fag, the conclusion follows. If there is a vertex y 2 V fag such that (a; y) 62E, then (y; a) 2 E: Let b1; b2; : : : ; bk be the vertices of D such that (a; bi) 2 E for i = 1; 2; : : : ; k: If y beats all the vertices that a beats, then score(y) > score(a) which is a contradiction. Therefore, there is a bi for some i 2 f1; 2; : : : ; kg such that (bi; y) 2 E: The conclusion now follows.

19.Prove that if D is a tournament, then it has a directed Hamiltonian path.

19. The proof is by induction on the number of vertices p in the tournament. Check all tournaments on 1, 2, 3, or 4 vertices and verify that each contains a Hamiltonian path. So assume that each tournament of order n where n 4 contains a Hamiltonian path and consider a tournament T of order n + 1:

Let v 2 V (T ): < V (T fvg) is a tournament of order n: By the induction hypothesis, < V (T ) fvg) contains a Hamiltonian path, say P : v1; v2; : : : ; vn: Now if (v; v1) is an edge of T , then T contains a Hamiltonian path v; v1; v2; : : : ; vn: If (vn; v) is an edge of T , then T contains a Hamiltonian path. So suppose (v1; v) is an edge of T: If all the vertices v1; v2; : : : ; vn are adjacent to v; then T contains a Hamiltonian path because (vn; v) is an edge of T: If not all the vertices v1; v2; : : : ; vn are adjacent to v; then there must be a vertex vi where 1 i n 1 such that (vi; v) and (v; vi+1 ) are edges of T: Then, v1; v2; : : : ; vi; v; vi+1; : : : ; vn is a Hamiltonian path.