
ДискретнаяМатематика / Student Solutions Manual / chapter 8
.pdf
8.2 Exercises
1.Suppose that is a sample space with a probability density function p and that E :
(a)Prove that 0 P (E) 1:
(b)What is the probability of the singleton event E = f!g?
(c)What is the probability of the event E = ?
1. (a) Since P (E) = !2E p(w) and since each p(!) 0, it follows that P (E) 0 and that P (E) !2 p(!) = 1.
1. (b) We have P (E) = !2E p(!) = p(!).
1.(c) We have P (E) = !2E p(!) = !2 p(!) = 1 .
3.Consider a sample space consisting of ve outcomes
f!1; !2; !3; !4; !5g
Which (if either) of the following functions p1 and p2 can be probability densities on ? Explain your answer.
|
! |
p1(!) |
p2(!) |
|
|
|
|
|
|
|
||
|
|
1=2 |
|
|
p |
|
|
|
|
|
|
|
|
!1 |
1=(3p |
7) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!2 |
1=4 |
2=(3p |
7) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!3 |
1=4 |
1=(3p |
7) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!4 |
1=2 |
2=(3 |
7) |
|
|
|
|
||||
|
|
|
p |
|
|
|
|
|
p |
|
|
|
|
!5 |
1=2 |
( 7 2)= 7 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Function p1(!) is not a probability density function because p1(!1) is negative. Function p2(!) is a probability density function: the value of p2 on each outcome is between 0 and 1, and the sum over all the outcomes of the value of p2 is 1.
5.A penny, a nickel, and a dime are shaken together and thrown. Someone proposes the sample space = f1; 5; 10g, explaining that the outcomes represent the values of the coins. Then, the person suggests the probability density function p(1) = p(5) = p(10) = 1=2, explaining that since the coins are fair, a uniform probability density is appropriate. Comment on several aspects of this situation. Do you agree with this model?
5. Since there are three outcomes in , a uniform probability density function assigns a value of 1/3, not 1/2, to each outcome. Note also that 1/2 + 1/2 + 1/2 does not sum to 1, so the function proposed is not a probability density function.
440
7. Given the sample space
= f0; 5; 10; 15; 20g
which of the following events are in the sample space?
(a)f5, 10g
(b)f0, 5, 10, 15, 20g
(c);
(d)0
(e)f0g
(f)f5g
7. All are events in except for (d), which is an outcome, not an event; the singleton event whose only outcome is 0 is given by (e).
9.For the two nickels and the dime in Exercise 8, there are eight possible combinations of heads and tails: tails on all coins; heads on nickel 1, tails on nickel 2, tails on the dime; and so on.
(a)Assuming that each of these eight combinations is equally likely, what probability density should be assigned to the sample space of Exercise 8? Specify the probability density by giving its value on each ! 2 :
(b)Invent a new sample space such that each of the situations in Exercise 8 can be described as an event, and specify a reasonable probability density for the new sample space.
(c)Describe each of the situations in Exercise 8 as an event in the new sample space from part (b).
(d)Calculate the probability of each of the events in part (c) using the new probability density.
9. (a) The probability of the outcome 0 is the probability that all coins land tails, which is 1/8. Hence, p(0) = 1/8.
The probability of the outcome 5 is the probability of nickel 1 landing heads and nickel 2 and the dime landing tails, plus the probability of nickel 2 landing heads and the other two coins landing tails. Hence, p(5) = 1/8 + 1/8 = 1/4.
The probability of the outcome 10 is the probability that both nickels land heads and the dime lands tails plus the probability that both nickels land tails and the dime lands heads. Hence, p(10) = 1/8 + 1/8 = 1/4.
The probability of the outcome 15 is the probability that nickel 1 lands tails and the other two coins land heads plus the probability that nickel 2 lands tails and the other two coins land heads. Hence, p(15) = 1/8 + 1/8 = 1/4.
442
The probability of the outcome 20 is the probability that all coins land heads. Hence, p(20) = 1/8.
9. (b) Let 1 consist of the eight ordered triples specifying heads or tails for nickel 1, nickel 2, and the dime, respectively:
!1 = (H; H; H), !2 = (H; H; T ), !3 = (H; T; H),
!4 = (T; H; H), !5 = (H; T; T ), !6 = (T; T; H), !7 = (T; H; T ), !8 = (T; T; T ).
Since the eight possibilities are equally likely to occur, the probability density function p(wi) has the value 1/8 on each outcome !i, for 1 i 8.
9. (c) The event \no heads" = f(T; T; T )g = !8. The event \all heads" = f(H; H; H)g = !1.
The event \exactly one head" =
f(H; T; T ); (T; H; T ); (T; T; H)g = f!5; !6; !7g
The event \exactly one nickel turns up heads" =
f(H; T; H); (H; T; T ); (T; H; H); (T; H; T )g = f!3; !4; !5; !7g
The event \dime turns up heads" =
f(H; H; H); (H; T; H); (T; H; H); (T; T; H)g = f!1; !3; !4; !6g
9. (d) The probability of \no heads" = 1/8. The probability of \all heads" = 1/8.
The probability of \exactly one head" = 3/8
The probability of \exactly one nickel turns up heads" = 4/8 = 1/2 The probability of \dime turns up heads" = 4/8 = 1/2
These probabilities are obtained by multiplying the number of outcomes in the event by the uniform density value 1/8
11.A small zoo records the proportions of visitors who prefer various animals as their favorites. Suppose that the elephants are preferred by 15%, the monkeys by 25%, the polar bears by 30%, the seals by 20%, and the boa constrictors by 10%. Suppose we are going to select a visitor at random and ask what animal that person prefers.
(a)Set up a sample space ; and de ne a probability density on it using the given data.
(b)Reformulate the descriptions of the following events as subsets of :
(i)The preferred animal has four legs.
(ii)The preferred animal has legs.
(iii)The preferred animal has either a trunk or ippers.
443
(c) Calculate the probability of each event in part (b). 11. (a) Let = f!1; !2; !3; !4; !5g, where
!1 is the outcome that a person prefers the elephants
!2 is the outcome that a person prefers the monkeys
!3 is the outcome that a person prefers the polar bears
!4 is the outcome that a person prefers the seals
!5 is the outcome that a person prefers the boa constrictors p(!1) = :15, p(!2) = :25, p(!3) = :30, p(!4) :20, p(!5) = :10 11. (b)
(i)E = \The animal has four legs" = f!1; !3g
(ii)E = \The animal has legs" = f!1; !2; !3g
(iii)E = \The animal has a trunk or ippers" = f!1; !4g
11. (c)
(i)P (E) = .15 + .30 = .45
(ii)P (E) =.15 + .25 + .30 = .70
(iii)P (E) = .15 + .20 = .35
(iv)P (E) = .10
13.Suppose that ve names are drawn from a hat at random and listed in the order in which they are drawn. A name on the list is \out of order" if its position is not the same as its position after the list has been alphabetized. Determine the probability of each of the following:
(a) Exactly two names are out of order.
(b) Exactly one name is out of order.
(c) At least two names are out of order.
13. (a) Let the sample space consist of all the 5! possible orders in which the ve names could be drawn. Assume each of these outcomes is equally likely, so each outcome has probability 1=(5!) = 1=120:
13 (b) Invent a new sample space such that each of the situations in Exercise 8 can be described as an event, and specify a reasonable probability density for the new sample space.
(i)There are C(5; 3) ways to choose the three names that are in the correct order. The remaining two names must be swapped (otherwise, all the names would be in correct order). Hence, specifying which three names are in correct order determines exactly one outcome in which the remaining two names are not in correct order. Thus, there are C(5; 3) = 10 outcomes of this type, each with probability 1/120. Thus, P (\exactly two names out of order") = 10/120 = 1/12.

445
(ii) Invent a new sample space such that each of the situations in Exercise 8 can be described as an event, and specify a reasonable probability density for the new sample space.
13. (c) The event E = \at least two names are out of order" is the complement of the event E = \at most one name is out of order", so P (E) = 1 - P (E 1 bad). Since it is impossible for exactly one name to be out of order, the event E 1 bad is the same as the event \no names are out of order", which consists of a single outcome. Hence, P (E 1 bad)
=1/120 and P (E) = 1 - 1/120 = 119/120.
15.Suppose A and B are events in a sample space such that P (A) = 1=4; P (B) = 5=8; and P (A [ B) = 3=4: What is P (A \ B)?
15.Since P (A [ B) = P (A) + P (B) - P (A \ B), we have 3/4 = 1/4 + 5/8 - P (A \ B), so rearranging terms gives P (A \ B) = 1/8.
17.Four cards are dealt at random from a deck. What is the probability that at least one of them is an ace? The answer may be given in terms of the binomial coe cient C(a; b):
17.Imagine that the cards are numbered 1 - 52. Let the sample space consist of all 4-element subsets of these numbers. Thus, there are C(52; 4) outcomes in , and since they are equally likely to occur, each has probability 1/C(52; 4).
The event E = \at least one of the four cards is an ace" is the complement
|
|
of the event E = \none of the four cards is an ace". Thus, P (E) = 1 - |
|
|
|
P (E). |
To determine P (E), note that the number of 4-element subsets |
containing no ace is C(48; 4), as all four cards must be chosen from the 48
cards that are not aces. Hence, P (E) = C(48; 4)=C(52; 4) and P (E) = 1
-C(48; 4)=C(52; 4).
19.The waiting room of a dentist's o ce contains a stack of 10 old magazines. During the course of a morning, four patients, who are waiting during nonoverlapping times, select a magazine at random to read. Calculate in two ways the probability that two or more patients select the same magazine.
19. Number the magazines 1 - 10, and let the sample space consist of ordered 4-tuples indicating the magazine choice of each patient. There are 410 outcomes in . The event that two or more patients select the same magazine is the event whose outcomes contain some number of numbers in the range 1-10 at least twice. This event is the disjoint union of the following events:
447
= \the same magazine is chosen by all four patients", whose probability is 1=(104);
Eexactly three same = \the same magazine is chosen by exactly three patients", whose probability is C(4; 3)(10)/104;
Etwo same = \the same magazine is chosen by two patients, and the other patients choose two other, di erent magazines". This event has probability C(4; 2)(10)(9)(8)/104 = 4320/104. Here C(4; 2) is the number of ways to pair two of the patients and then to follow this pair with the two other patients, say in alphabetical order. The pair of patients can choose a magazine in 10 ways, the rst single patient can choose from the remaining magazines in 9 ways, and the last second patient can choose from 8 magazines.
Let Etwo same twice = \two magazines are chosen; one is chosen by two patients and the other is chosen by the other two patients". The proba-
bility of this event is P (Etwo same twice) = C(4; 2)(10)(9). Here, C(4; 2) is the number of ways to arrange four patients into two pairs, where the
pairs are given in some order. For example, we regard the ordered list of pairs (1,2),(3,4) as the same as the ordered list of pairs (2,1),(3,4), but we regard the list (1,2),(3,4) as di erent from the list (3,4),(1,2), because which pair comes rst matters. However, the 2-tuple giving a pair is not regarded as an ordered 2-tuple. The number of ways that the rst pair on the list may be assigned a magazine is 10; since the second pair on the list must read a di erent magazine, there are 9 ways to assign the second magazine.
All together, then, the probability that two or more patients choose the same magazine is
( 1 + C(4; 3)(10) + 4320 + C(4; 2)(10)(9) )= 104
A di erent way to calculate this is as follows:
Let E be the event \no two patients select the same magazine", whose probability is (10)(9)(8)(7)/ 104. Then, the probability that two or more patients select the same magazine is 1 - P (E) = 1 - ( (10)(9)(8)(7)/ 104 ).
21.Suppose E1; E2; : : : ; En are events (not necessarily disjoint) in a sample space endowed with a probability density p. Find an expression for P ([1 i n Ei); and prove that the expression is valid. (Hint. Make an analogy to the Principle of Inclusion-Exclusion of Section 1.5, but add up probabilities instead of elements.)
21. Let E denote the event [1 i n Ei. Of course P (E) = !2E p(!). To compute P (E), we look for an expression involving sums and di erences of the P (Ei) such that when terms are collected, the multiplier for each p(!) such that ! 2 is 1, and the multiplier for any p(!) such that ! 2= is 0. To explore this approach, consider the following expression:
P (E1) + P (E2) + + P (En)
449
Imagine the expression written out in terms of sums of p(!)'s. Each ! 2 E that appears in exactly one of the Ei's contributes its p(!) exactly once to the sum. However, many p(!)'s appear with multipliers bigger than 1. For example, if ! belongs to exactly two of the E's, say E1 and E2, then its probability is added in two times, once in the expression for P (E1, and once more in the expression for P (E2). To correct this situation, consider the following modi ed expression:
P (E1) + P (E2) + + P (En)
P (E1 \ E2) P (E1 \ E3) P (E1 \ En) P (En 1 \ En)
Here we have subtracted from the previous expression the probability of each event of the form Ei \ Ej for distinct i and j. Now each ! 2 E that belongs to exactly two of the E's, say E1 and E2, contributes p(!) to the expression for E1, another p(!) to the expression for E2, but then has p(!) taken away by the expression P (E1 \ E2). Thus the multiplier for p(!) is 1, as desired.
Furthermore, any ! 2 E that belongs to exactly one of the Ei contributes p(!) exactly once, as before.
However, a problem still remains. Suppose some ! 2 belongs to exactly three of the Ei's. It contributes p(!) three times in the sum of the P (Ei), but then p(!) is subtracted three times by the terms of the form P (Ei \ Ej ). Thus its multiplier is 0.
Undaunted, we correct for this by adding in the probabilities of events of the form Ei \ Ej \ Ek for distinct i; j; k. It can be checked that this corrects the latest problem without disturbing the multipliers of outcomes in exactly one or exactly two of the Ei's. This gives a new expression
P (E1) + P (E2) + + P (En)
P (E1 \ E2) P (E1 \ E3) P (E1 \ En) P (En 1 \ En)
+P (E1 \ E2 \ E3 + + P (E1 \ E2 \ En) + + P (En 2 \ En 1 \ En)
Continuing this reasoning process, we eventually arrive at a correct expression for P (E):
P (E) = 1 i n P (Ei)
1 i<j n P (Ei \ Ej )
+ 1 i<j<k n P (Ei \ Ej \ Ek )
450
: : : + ( 1)n 1P (E1 \ E2 \ \ En)
The correctness of this expression can be established by checking that for 1 k n, any ! appearing in exactly k of the Ei's has multiplier 1; clearly any ! not belonging to E does not appear in any term and contributes nothing.
8.4 Exercises
1.Suppose S is a set with k elements. How many elements are in Sn; the cross product S S S of n copies of S?
1. kn
n |
m |
l |
3. Suppose Pi=1 ai = 2; |
Pj=1 bj = 3; and |
Pk=1 ck = 5: Evaluate |
nm l
XX X
ai( |
bj ck ): |
i=1 |
j=1 k=1 |
3.
nm l
XX X
ai( bj ck )
i=1 j=1 k=1
n m |
l |
X X |
X |
= ai( bj )( ck )
i=1 j=1 k=1 n m
X X
= 5 ai( bj )
i=1 j=1 n
X
= 5 3 ai
i=1
= 5 3 2 = 30
453
5.Suppose that people are equally likely to be born on each of the seven days of the week. In a group of n people, what is the probability that:
(a)Two or more of them were born on Saturday.
(b)Exactly two of them were born on Saturday.
(c)Two or more of them were born on the same day of the week.
5. (a) C(n; 2)(1=7)2(6=7)n 2 +C(n; 3)(1=7)3(6=7)n 3 + +C(n; n)(1=7)n
5. (b) C(n; 2)(1=7)2(6=7)n 2
5.(c) If n > 7; the probability is 1. If n = 7; then the problem is similar to the birthday problem, 1 (7 6 (7 n + 1))=7n:
7.A coin is tossed, a die is rolled, and a card is drawn at random from a deck. Assume that the toss, roll, and draw are fair.
(a) Describe this experiment as a cross product sample space.
(b) With the aid of a tree diagram, de ne a probability density on the cross product.
(c) Verify by direct computation that the probability density found in part
(b) is legitimate.
(d) Does it matter in what order the coin, the die, and the card are considered?
7.(a)
= fH, Tg f1; 2; 3; 4; 5; 6g
fAce Clubs, 2 Clubs, . . . , King Spadesg
An outcome has the form (x; y; z) where x 2 1, y 2 2, and z 2 3:
7. (b) Since the coin and the die are fair and the cards of the deck are equally likely, de ne p(x) = (1=2) (1=6) (1=52) for ! 2 1 2 3:
7. (c) 1 p(!) 0 for each ! 2 1 2 3:
X
p(!) = 1 1 1 = 1
!2 1 2 3
7.(d) The order in which the cross product is formed does not matter.
9.A coin that is twice as likely to show heads than it is tails is tossed three times.
(a)Describe this experiment as a Bernoulli process.
(b)Use a tree diagram to assign a probability density.
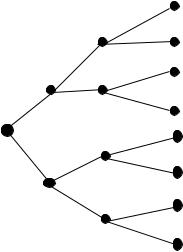
456
9. 1 = fH; T g:
9. (a) 1 1 1
9. (b)
H
H
T
H
H
T
T
H
H
T
T
H
T
T
Flip 1 Flip 2 |
Flip 3 |
8/27
4/27
4/27
2/27
4/27
2/27
2/27
1/27
11.A coin that is twice as likely to show heads than it is tails is tossed three times. Suppose we are only interested in the number of heads.
(a)Formulate this experiment in terms of a sample space with outcomes that give the number of heads.
(b)Assign a probability density function to this sample space.
(c)Describe the event \at least two heads" as a set of outcomes in this sample space.
(d)What is the probability of the event in part (c)?
