
ДискретнаяМатематика / Student Solutions Manual / chapter 8
.pdf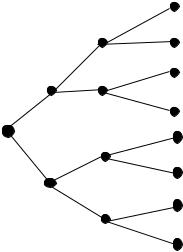
458
11.
H 8/27
H
4/27
T
H 4/27
H
T
T 2/27
H 4/27
H
T
2/27
T
H 2/27
T
T
1/27
Flip 1 |
Flip 2 |
Flip 3 |
|
|
11. (a) = f0; 1; 2; 3g
11.(b) p(0) = (1=3)3 p(1) = 3(2=3)(1=3)2
p(2) = 3(2=3)2(1=3) p(1) = 3(2=3)3(1=3)0
11. (c) E = f2; 3g
11.(d) p(E) = p(2) + p(3) = 3(2=3)2(1=3) + (1=3)3 = (4=9) + (1=27) = (13=27)
13.For the cross product sample space found in Exercise 8 (a), give the cross product formulation, and calculate the probability of each of the following events:
(a)An even number of spots shows on each of the die.
(b)The loaded die shows six spots.
(c)The fair die shows either ve or six spots, and the loaded die shows six spots.
13.Fair die has sample space 1 = f1; 2; 3; 4; 5; ; 6g with p1(i) = (1=6) for 1 i 6: The loaded die has sample space 2 = f1; 2; 3; 4; 5; 6g with p2(i) = (1=10) for 1 i 5 and p2(6) = (1=2):
13. (a) E = f(2, 2), (2, 4), (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6, 4), (6, 6)g. This is f2; 4; 6g f2; 4; 6g:
459
p((2; 2)) = (1=60) p((2; 4)) = (1=60) p((2; 6)) = (1=12) p((4; 2)) = (1=60) p((4; 4)) = (1=60) p((4; 6)) = (1=12) p((6; 2)) = (1=60) p((6; 4)) = (1=60) p((6; 6)) = (1=12)
p(E) = p((2; 2)) + p((2; 4)) + + p((6; 6)) = 7=20
13. (b) E = f(i; 6) : 1 i 6g: p((i; 6)) = (1=12) for 1 i 6: Therefore, P (E) = 6(1=12) = (1=2).
13.(c) E = f(5; 6); (6; 6)g. p(E) = p1(5)p2(6) + p1(6)p2(6) = (1=12) + (1=12) = (1=6)
15.Give two ways you could label the outcomes of an experiment that consists of ipping a dime three times. Determine a probability density function for each of the two ways.
15.Count the number of heads or label each ip separately and consider three tuples
17.Suppose the sex of a newborn child is viewed as an experiment with two equally likely outcomes. Assuming that each child represents an independent trial, what is the probability of a family with four children having two, three, or four girls? Suppose the probability of the child being a girl is 0.52; now what is the probability of two, three, or four boys?
17. 4 girls = 1/24 = 0.0625
2 girls: C(4; 2)(1=2)2(1=2)2
3girls: C(4; 3)(1=2)3(1=2) 2 boys: C(4; 2)(:52)2(:48)2
3boys:: C(4; 3)(:48)3(:52) 4 boys: C(4; 4)(:48)4
8.6 Exercises |
461 |
1.A sample space = f!1; !2; : : : ; !6g has the following probability density de ned on it:
p(!1) = 2=5 p(!4) = 1=10 p(!2) = 1=10 p(!5) = 1=10 p(!3) = 1=5 p(!6) = 1=10:
Which of the following pairs A; B of events are independent? Explain your answer.
(a)A = f!1; !2g and B = f!3; !5g
(b)A = f!1; !6g and B = f!2; !6g
(c)A = ; and B = f!3; !4; !5g
(d)A = f!1; !3g and B = f!3; !4; !5g
1. (a) P(A) = (2/5) + (1/10) = (1/2)
P(B) = (1/5) + (1/10) = (3/10)
P(A \ B) = P(;) = 0
P(A)P(B) = (1/2) (1/10) = (3/10)
Not independent
1. (b) P(A) = (2/5) + (1/10) = (1/2) P(B) = (1/10) + (1/10) = (1/5) P(A \ B) = P (!6) = (1/10)
P(A) P(B) = (1/10) Independent
1. (c) P(;) = 0
P(B) = (1/5) + (1/10) + (1/10) = (2/5)
P(A \ B) = P(;) = 0
P(;) P(B) = 0 (2/5) = 0
Independent
1. (d) P(A) = (2/5) + (1/5) = (3/5)
P(B) = (1/5) + (1/10) + (1/10) = (2/5)
P(A \ B) = P(!3) = (1/5)
P(A)P(B) = (3/5) (2/5) = (6/25)
Not independent
3.Suppose A and B are disjoint events in a sample space : Is it possible that A and B could be independent? Explain your answer.
3. If P (A) = 0 or P (B) = 0, then A and B are independent.

463
5.Suppose that E1; E2; : : : ; Ek are events in the same sample space and that some pair Ei; Ej of these events are disjoint.
(a)If all the events have positive probability, can the set fE1; E2; : : : ; Ek g be an independent set of events? Explain your answer.
(b)If one or more of the events has 0 probability, can the set fE1; E2; : : : ; Ek g be an independent set of events?
5. (a) Since P (E1 \E2 \ \Ek ) = P (;) = 0 and P (E1)P (E2) P (Ek ) > 0 since P (Ei) > 0 for 1 i k, the events cannot be independent.
5. (b) The events may be independent, but they need not be.
7.Suppose that is a sample space with a probability density function p, and suppose that A : Let P (A) denote the probability of A. Assume that P (A) > 0: De ne a function p1 on A as follows: For ! 2 A, p1(!) = p(!)=P (A).
(a) Show that if !1; !2 2 A and p(!1); p(!2) 6= 0; then
p(!1) = p1(!1) p(!2) p1(!2)
(b) Show that if B and C are nonempty subsets of A with elements that have positive probabilities, then
P (B) = P1(B)
P (C) P1(C)
(c) Show that p1 is a probability density function on 1 = A:
7. (a)
p1(!1) = p1(!2)
7. (b)
P1 |
(B) |
|
|
P!2B p(!) |
|||
= |
|
|
P (A) |
|
|||
P1(C) |
|
|
P p(! |
||||
|
|
|
!2C |
|
|||
P (A)
( pP((!A1)) ) |
= |
p(!1) |
|
|||||
|
p(!2 |
|
p(!2) |
|
|
|||
|
|
|
||||||
( |
P (A) |
) |
|
|
||||
= P!2C p(!) = |
P (C) |
|||||||
|
|
!2B p(!) |
P (B) |
|||||
P
7. (c) p1(!) = p(!) 0 since p(A) > 0 and p(!) 0: p1(!) 1 since
P (A)
p(!) p(A):
!2A p1 |
(!) = !2A |
P (A) |
= |
P (A) |
!2A p(!) = |
P (A) P (A) = 1 |
|||
X |
X |
|
p(!) |
|
1 |
|
X |
1 |
|
465
9.A television show features the following weekly game. A sports car is hidden behind one door, and a goat is hidden behind each of two other doors. The moderator of the show invites the contestant to pick a door at random. Then, by tradition, the moderator is obligated to open one of the two doors not chosen to reveal a goat (there are two goats, so there is always such a door to open). At this point, the contestant is given the opportunity to stand pat (do nothing) or to choose the remaining door. Suppose you are the contestant, and suppose you prefer the sports car over a goat as your prize. What do you do? (Hint: It may help to model this as a two stage dependent trials process, but it may not be obvious how to do this.)
(a)Suppose you decide to stand with your original choice. What are your chances of winning the car?
(b)Suppose you decide to switch to the remaining door. What are your chances of winning the car?
(c)Suppose you decide to ip a fair coin. If it comes up heads, you change your choice, otherwise, you stand pat. What are your chances of winning the car?
9. (a) 1/3
9. (b) 2/3
9. (c) 1/2
NOTE: The answer to the goat problem is 2/3 for the switching strategy, 1/3 for the do-nothing strategy, and 1/2 for the coin ip strategy.
Under the switch strategy, the only time you lose is if you originally chose the car. Then you switch to a goat. But you only picked the car originally 1 time in 3. So you only lose 1 time in 3 { hence, win 2 times in 3.
If you do nothing, your chance is 1 in 3. If you ip, you know you will be choosing between 1 goat and 1 car, so your chances are 1 in 2.
11.(a) Give an example that shows three pairwise independent events need not be an independent set of events.
(b) Give an example that shows three events can be independent without having the corresponding pairs of events be independent.
11. (a) Flip a fair coin three times. Let Ai;j be the event that the ith and jth ips show the same face. Let
= f(T; T; T ); (T; T; H); ; (H; H; H)g be the sample space of the experiment. Then
A1;2 = f(T; T; T ); (T; T; H); (H; H; T ); (H; H; H)g
A1;3 = f(T; T; T ); (T; H; T ); (H; T; H); (H; H; H)g
A2;3 = f(T; T; T ); (H; T; T ); (T; H; H); (T; T; T )g

467
Since j j = 8 and the coin is fair, the probability of each outcome is 18 . The probability of an event is given by the sum of the probabilities of the outcomes in the event. Thus,
1 P (A1;2) = P (A1;3) = P (A2;3) = 2 :
We now show that the events are pairwise independent.
1
P (A1;2 \ A1;3) = P (f(T; T; T ); (H; H; H)g) = 4 = P (A1;2)P (A1;3)
1
P (A1;2 \ A2;3) = P (f(T; T; T ); (H; H; H)g) = 4 = P (A1;2)P (A2;3)
1
P (A1;3 \ A2;3) = P (f(T; T; T ); (H; H; H)g) = 4 = P (A1;;3)P (A2;3):
Thus, the events are pairwise independent. However,
P (A1;2 \ A1;3 \ A2;3) = P (f(T; T; T ); (H; H; H)g)
= 1=4 6= 1=8
= P (A1;2)P (A1;3)P (A2;3)
Thus, the set of events is not independent.
11. (b) Flip a fair coin three times. Let A1;2 and A1;3 be de ned as in part (a). De ne a new event B as follows:
B = f(T; T; T ); (H; T; T ); (T; H; H); (T; T; H)g
Note that P (B) = 1=2.
P (A1;2 \ A1;3 \ B) = P (f(T; T; T )g) = 1=8 = P (A1;2)P (A1;3)P (B) Thus the set of events is independent. We now show that the events are
not pairwise independent. |
|
|
|
|
|
P (A1;3 \ B) = P (f(T; T; T )g) = |
1 |
6= |
1 |
= P (A1;3)P (B) |
|
|
|
|
|||
8 |
4 |
|
|||
Thus the set of events are not pairwise independent.
13.When a roulette wheel is spun once, there are 38 possible outcomes: 18 red, 18 black, and 2 green (if the outcome is green the house wins all bets). If a wheel is spun twice, all 38 38 outcomes are equally likely. If you are told that in two spins at least one resulted in a green outcome, what is the probability that both outcomes were green?
13. P (second green j rst green) + P ( rst green j second green) = ((2 2)=(38 38))=((1=38) + (1=38) (1=(38)2)) = 4=75
468
15.Only 1 in 1000 adults is a icted with a particular rare disease for which a diagnostic test has been developed. The test is such that when an individual actually has the disease, a positive result will occur 99% of the time, and an individual without the disease will show a positive test result only 2% of the time. If a randomly selected individual is tested and the result is positive, what is the probability that the individual has the disease? Draw a tree diagram for the problem.
15. Let A1 denote the event that the individual has the disease; let A2 denote the event that the individual does not have the disease; let B denote the event of a positive result.
P (A1) = :001; P (A2) = :999; P (BjA1) = :999; P (BjA2) = :02; P (B) = :00099 + :01998 = :02097; P (A1jB) = P (A1 \ B)=P (B) = :00099=:02097
=:047
17.We toss two fair dice and assume a uniform probability density function on the 36 ordered pairs in the sample space. What is the probability that the sum is 9, given that the rst die comes up 5?
17. Let F5 denote the event that the rst die comes up 5, and let S9 denote the event that the sum is 9.
P (S9jF5) = P (S9 \ F5)=P (F5)
But
S9 \ F5 = f(5; 4)g
and
F5 = f(5; 1); (5; 2); (5; 3); (5; 4); (5; 5; (5; 6)g
Hence, P (S9 \ F5) = 1=36 and P (F5) = 6=36. Thus P (S9jF5) = 1=6. Similarly, we may compute
P (F5jS9) = P (F5 \ S9)=P (S9)
and since
S9 = f(6; 3); (5; 4); (4; 5); (3; 6)g
we see that
P (S9) = 4=36 andP (F5jS9) = 1=4
470
8.8 Exercises
1.Consider a game based on the days of a 31-day month. A day is chosen at random{say, by spinning a spinner. The prize is a number of dollars equal to the sum of the digits in the date of the chosen day. For example, choosing the 31st of the month pays $3 + $1 = $4, as does choosing the fourth day of the month.
(a)Set up the underlying sample space and its probability density, the value of which at ! gives the reward associated with !..
(b)De ne a random variable X(!) on with value at ! that gives the reward associated with !:
(c)Set up a sample space X consisting of the elements in the range of X, and give the probability distribution pX on X arising from X:
(d)Determine P (X = 6):
(e)Determine P (2 X 4) = P (! : 2 X(!) 4):
(f)Determine P (X > 10) = P (! : X(!) > 10):
1. (a) Let = f01; 02; ; 31g be the sample space associated with the experiment. Since we are choosing a day at random we have a uniform probability density. In particular, p(!) = 1=31 for all ! 2 .
1. (b) We can think of an element in as the concatenation of two digits so that ! = ij for all ! 2 , for some i; j 2 f0; 1; ; 9g. Then X(!) = X(ij) = i + j for all ! 2 .
1. (c) X = f1; 2; ; 11g pX (1) = P (f01; 10g) = 2=31
pX (2) = P (f02; 20; 11g) = 3=31 pX (3) = P (f03; 30; 12; 21g) = 4=31 pX (4) = P (f04; 31; 13; 22g) = 4=31 pX (5) = P (f05; 14; 23g) = 3=31 pX (6) = P (f06; 15; 24g) = 3=31 pX (7) = P (f07; 16; 25g) = 3=31 pX (8) = P (f08; 17; 26g) = 3=31 pX (9) = P (f09; 18; 27g) = 3=31 pX (10) = P (f19; 28g) = 2=31
pX (11) = P (f29g) = 1=31
1. (d) P (X = 6) = pX (6) = 3=31
1. (e) P (2 x 4) = pX (2) + pX (3) + pX (4) = 11=31 1. (f) P (X > 10) = pX (11) = 1=31
471
3.Suppose we ip a fair coin four times. We are interested in counting the number of times the coin turns up heads.
(a)De ne a sample space and a probability density p on :
(b)De ne a random variable X on to count the number of heads.
(c)Describe the event (X = 3) as a subset of :

472
(d)Set up a sample space X and a probability distribution pX based on X: You may express your answer in terms of the binomial distribution.
(e)Which number (or numbers) of heads is most likely to occur?
3. (a) We use the usual sample space consisting of the 24 possible sequences of heads and tails. Let 1 denote heads and 0 denote tails. Then,
= f(x1; x2; x3; x4jxi 2 f0; 1gg
Since the coin is fair we have a uniform probability density p(!) = j1 j = 1=16 for all ! 2 .
3. (b) Let the random variable X be de ned on by setting X(!) equal to the number k of times heads occurs in the 4-tuple !.
X(!) = X(x1; x2; x3; x4) = x1 + x2 + x3 + x4
3. (c) The event (X = 3) is given by the set
f(1; 1; 1; 0); (1; 1; 0; 1); (1; 0; 1; 1); (0; 1; 1; 1)g
3. (d) The sample space X is the range of X and is given by f0; 1; 2; 3; 4g. It is important to recognize that the distribution pX of X is the Bernoulli distribution. Thus, pX (k) = C(n; k)pk (1 p)n k for k 2 X . Substituting n = 4 and p = 1=2 (since the coin is fair) into the equation and simplifying gives pX (k) = C(4; k)=16.
3. (e) To determine which number of heads is most likely we calculate pX (k) for each k 2 . pX (0) = 1=16, pX (1) = 1=4, pX (2) = 6=16, pX (3) = 1=4, pX (4) = 1=16. Thus, 2 is the most common number of heads.
5.What is the relationship between b(k; n; p) and b(n k; n; p) when p = 1=2? Does this relationship hold if p 6= 1=2?
5. If p is 1=2, then 1 p is also 1=2, so p = 1 p. Thus,
b(n k; n; p) = C(n; n k)pn k (1 p)n (n k)
= |
|
n! |
|
pn kpn (n k) |
||
(n k)!(n (n k))! |
||||||
|
|
|||||
|
= |
|
n! |
pn kpk |
||
|
|
(n k)!k! |
||||
|
|
|
|
|
||
= C(n; k)pk pn k
=C(n; k)pk (1 p)n k
=b(k; n; p)
