
ДискретнаяМатематика / Student Solutions Manual / chapter 6
.pdf
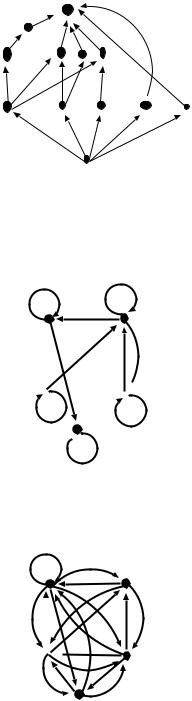
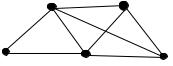
21. Show that the gure
1
7
2
6 
 3
3
5 |
4 |
|
can be used to schedule a \tournament" for seven players. The tournament has a directed edge (i; j) if and only if i beats j. (Hint: Rotate the edges but not the vertices.)
21. Schedule six rounds for the tournament with the games being between players i and j in round k as shown in the table.
Round 1 |
Round 2 |
Round 3 |
Round 4 |
Round 5 |
Round 6 |
|
||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
(2, 7) |
(1, 3) |
(2, 4) |
(3, 5) |
(4, 6) |
(5, |
7) |
|
|||||
(3, |
6) |
(4, |
7) |
(1, |
5) |
(2, |
6) |
(3, |
7) |
(1, |
4) |
|
(4, |
5) |
(5, |
6) |
(6, |
7) |
(1, |
7) |
(1, |
2) |
2, 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Each match will result in one edge being put in the tournament with edge (i; j) in the tournament if player i beats player j.
Representing a Relation. A digraph can be used to represent a relation. For a relation R on a set A de ne the digraph D = (V; E) as follows. Let V = A. There is an edge (i; j) 2 E if and only if (i; j) 2 R: The de nition of a digraph needs to be extended slightly to allow representation of elements of the form (x; x) 2 R: A loop in a digraph is an edge with both ends the same. We think of a loop as starting and ending at the same vertex. For example, we can represent the relation R on f1, 2, 3, 4, 5g with elements f(1, 1), (2, 3), (3, 4), (4, 1), (2, 5)g as
1
5 |
2 |
4 3
23.Represent by a digraph the partial order divides de ned on the integers 0 through 11.
23. |
|
0 |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
4 |
6 |
9 |
10 |
|
|
|
|
|
|
|
|
2 |
3 |
|
5 |
7 |
11 |
|
|
1
25.Let R be the relation on f1, 2, 3, 4, 5g with elements f(1, 1), (2, 1), (3,
2), (2, 3), (1, 4), (3, 5), (5, 2)g. Represent the re exive closure of R as a digraph.
25.
1 |
2 |
5 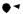

 3
3
 4
4
27. Let R be the relation on f1, 2, 3, 4g with elements f(1, 1), (2, 1), (3, 2), (2, 3), (1, 4)g. Represent the transitive closure R of R as a digraph.
27.
1 |
2 |
5 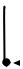
3
4
6.21 End of Chapter Materials
Starting to Review
1.A trail may contain
(a)Repeated occurrences of vertices and edges
(b)Repeated occurrences of vertices but no repeated occurrences of edges
(c)No repeated occurrences of vertices and no repeated occurrences of edges
(d)None of the above
1.b
3.Let D = (V; E) be a directed graph. An edge (a; b) 2 E:
(a) Contributes one to the indegree of a
(b) Contributes one to the outdegree of a
(c) Contributes one to the indegree of a and one to the outdegree of b
(d) All of the above
3.b
5.Construct a graph with degree sequence 1, 2, 2, 3, 4, 5, or prove that none exists.
5.None exists because there are an odd number of vertices with odd degree.
7.Find an MCST in G. Show all the steps of the algorithm you use.
a b 3
4 |
6 |
1 6
|
|
5 |
|
e |
5 |
7 |
c |
d |
7.
STEP 1: (a, d) 1
STEP 2: (a, b) 3
STEP 3: (a, e) 4
STEP 4: (a, c) 6

9. Find an Eulerian circuit in G. Show all steps of the process.
2 |
3 |
|
|
10 |
|
1 |
7 |
8 |
4 |
|
9 |
||
|
|
|
6 |
5 |
|
G
9.
2 |
3 |
|
|
10 |
|
1 |
7 |
8 |
4 |
|
9 |
||
|
|
|
|
6 |
|
5 |
|
|
|
|
|
|
2 |
|
3 |
2 |
3 |
|
|
|
||
|
|
|
|
|
|
|
10 |
|
|
|
|
10 |
|
1 |
|
7 |
8 |
4 |
1 |
7 |
8 |
4 |
|
|
9 |
|
|
|
9 |
||
|
|
|
|
|
|
|
||
|
6 |
5 |
|
|
|
6 |
5 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1-2-3-4-5-6-1 |
|
|
|
|
2-6-3-10-8-9-7-10-9-5-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Spliced Euler Circuit |
|
|
|
|
|
|
|
|
1-2-6-3-10-8-9-7-10-9-5-2-3-4-5-6-1 |
|
|
|
|
||
Review Questions
1. Let G = (V; E) be a graph for which deg(v) r with r 2 for every v 2 V: Prove that G contains a cycle of length at least r + 1: Use this result to show that if everyone at a party knows at least n others, then it is possible to seat n + 1 of the guests at a circular table so that everyone know the persons seated on their left and their right.
1. Let u and v be the ends of a longest path P in g. If P has length greater than or equal to k, the result follows. If not, then the ends of P are only adjacent to vertices of P else there would be a longer path. Since deg(v)k, there must be k vertices to which u is adjacent. In P there are only k 1 vertices. Therefore, there is a vertex x 2 V such that (x; u) 2 E: The path xP is longer than P . This is a contradiction.
CYCLE: Take P to be a longest path in G. The length of P is at least k by above. At least one adjacency x of u { an end vertex { must be at least k length from u. Then u x u is a cycle of length at least k + 1:

3. Prove that G and H are isomorphic.
1
7
6
9
10 |
2 |
|
|
a |
b |
|
8 |
d |
|
c |
||
e |
||
3 |
|
|
f |
g |
5 |
4 |
j |
i |
h |
|
||||
|
G |
|
H |
|
3.
F : V (G) ! V (H)
2! a
1! b
7! e
9! d
8! c
5! f
4! g
6! j
10 ! i
3! h
5.Construct the Df s and Bf s trees for the following graph shown starting at vertex 1. Assume the adjacency lists are formed by listing the adjacencies of each vertex in increasing order.
1
2
9
12
10 |
8
11
3
13 
14 |
15 |
4 |
|
7
5
6
5.
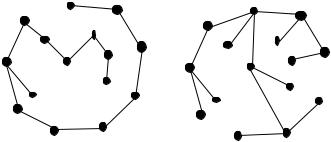
|
|
|
List of |
|
|
|
|
Vertices |
|
Adjacencies |
|
|
|
||
1 |
|
2 |
9 |
10 |
11 |
|
|
2 |
|
1 |
3 |
12 |
|
|
|
3 |
|
2 |
4 |
13 |
|
|
|
4 |
|
3 |
5 |
14 |
|
|
|
5 |
|
4 |
6 |
7 |
8 |
11 |
15 |
6 |
|
6 |
7 |
|
|
|
|
7 |
|
5 |
6 |
8 |
15 |
|
|
8 |
|
5 |
7 |
9 |
10 |
15 |
|
9 |
|
1 |
8 |
10 |
|
|
|
10 |
|
1 |
8 |
9 |
11 |
|
|
11 |
|
1 |
5 |
10 |
12 |
14 |
|
12 |
|
2 |
11 |
13 |
|
|
|
13 |
|
3 |
12 |
14 |
|
|
|
14 |
|
4 |
11 |
13 |
|
|
|
15 |
|
5 |
7 |
8 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
||
|
|
2 |
2 |
|
|
|
|
||
9 |
|
9 |
|
|
|
|
|
||
12 |
|
12 |
|
|
|
|
|
||
10 |
|
3 |
3 |
|
13 |
10 |
|||
|
13 |
|||
8 |
|
|||
|
|
|||
11 |
|
8 |
|
|
|
|
11 |
|
|
|
14 |
|
14 |
|
|
|
|
||
15 |
|
4 |
4 |
|
|
15 |
|||
|
|
|||
|
|
|
||
7 |
|
7 |
|
|
|
|
|
||
6 |
|
5 |
5 |
|
|
6 |
|||
|
|
|
||
dfs starting at 1 |
|
bfs starting at 1 |
|
|
|
|
|
7.Prove by induction that the sequence 1; 1; 2; 2; 3; 3; : : : ; n 1; n 1; n; n is graphical for all n such that n 1:
7. Prove this by induction. Let n0 = 1. Let T = fn 2 N : there exists a graph with degree sequence 1, 1, 2, 2, 3, 3, . . . ; n 1; n 1; n; ng
(Base step) For n = 1 the graph with two vertices and one edge works. Therefore, 1 2 T : For n = 2 the path with three edges works. Therefore, 2 2 T :
(Inductive step) Let n be chosen such that n > n0 + 1 so that n is not a base case and assume for all k such that n0 + m0 k < n that k 2 T : Now prove that n 2 T :
Since n0 + 1 n 2 < n by the induction hypothesis, there is a graph with degree sequence 1,1,2, 2, . . . , n 2; n 2: Let G = (V; E) be one such graph. Partition V into two sets V1 and V2 (since this is a partition V1 \ V2 = ;) such that both V1 and V2 contain n 2 vertices where the degrees of the vertices in each of the elements of the partition are 1, 2,
. . . , n 2. De ne a graph H such that H(V ) = V1 [ V2 [ fd1; d2; d3; d4g: De ne E(H) = E(G) [ f(d1; vi) : vi 2 V1 for 1 i n 2g [ f(d2; wi) : wi 2 V2 for 1 i n 2g [ f(d3; d1); (d4; d2); (d1; d2)g: H has degree sequence 1; 1; 2; 2; : : : ; n 1; n 1; n; n: Therefore, n 2 T :
By the Strong Form of Mathematical Induction, T = N f0g.
9.Prove that a graph is connected if and only if every two-part partition of the vertices of the graph has an edge with ends in both parts of the partition.
9.()) Let G = (V; E) be a graph. Suppose G is connected and V = V1[V2 is a 2-part partition. Let x 2 V1 and y 2 V2: G has a path from x to y. The rst edge on this path that has only one vertex in V1 must have its other vertex in V2.
(() Suppose every two-part partition of V has an edge with ends in both parts of the partition and that G is not connected. Then, there are vertices x; y 2 V such that there is no path from x to y . Let X = fz 2 V : z is connected to x by a pathg and let Y = V X = fw 2 V : w is not connected to x by a pathg. By hypothesis, there is an edge (u; v) with u 2 X and v 2 Y: But by de nition of X, there is a path from x to v and adding the edge (u; v) gives a path from x to u. But this is a contradiction since v 2 Y if there is no path from x to v. Thus, G must be connected.
11.Prove that if a tree has a vertex of degree p, then it has at least p vertices of degree one.
11. Let v be a vertex of degree p in a tree. Let its adjacencies be v1; v2; : : : ; vp. Each of these p vertices are distinct and there are no paths in the tree between any pair of these vertices. Either these vertices are leaves and have degree 1 or there is a path from each of these vertices to a leaf. These leaves are the p vertices of degree 1.
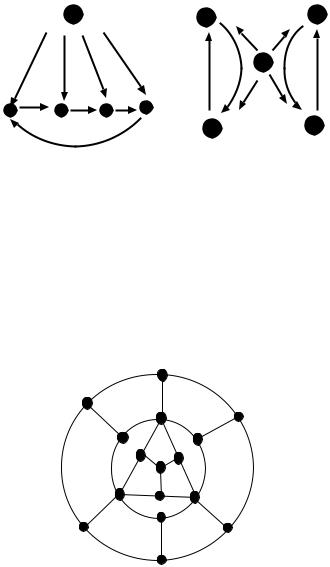
13. Prove that D1 and D2 are not isomorphic.
1 |
B |
D |
|
|
C |
2 |
5 |
|
|
3 |
4 |
|
E |
|
|
A |
|
D |
D |
|
2 |
||
1 |
||
|
13. Vertex 1 must be mapped to vertex C. (1, 2) must be mapped to an edge going out of C. The four edges out of C will all lead to the same result so suppose (1, 2) is mapped to (C, A). Now, (2, 3) must be mapped to (A, B) since (A, B) is the only edge out of A. The edge (3, 4) now cannot be mapped to anything that has B as head. Therefore, the graphs are not isomorphic.
15. Prove that G contains no Hamiltonian cycle.
G
15. Label the top most vertex with an A. Label its neighbors with B. Repeat this process until all the vertices are labeled. Any Hamiltonian cycle must go alternately through an A vertex and then a B vertex. There are too many A vertices for this to result in a Hamiltonian cycle.
Using Discrete Mathematics in Computer Science
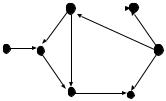
1.A vertex in a directed graph that has an indegree of zero is called a transmitter. Identity the transmitters in D. Devise a strategy for spreading a rumor so that all the nodes of the graph, which can be thought of as people on the ends of telephone lines, know the rumor.
c |
d |
|
|
|
|
b
a
e
g |
f |
D
1.a and e are transmitters. Tell each transmitter the message and have them transmit it to each of their adjacencies. When a vertex gets the message, for the rst time, it checks all its adjacencies to see if any have not received the message and transmits it on. If a vertex has already received the message and is told the message again, there is no need to transmit to any adjacency. Each vertex must only keep track of whether or not it has received the message to know whether to transmit it when it is told the message by another vertex.
3.A printer has one printing machine and one binding machine. Let pi and bi denote the printing time and binding time for book i, respectively. For any two books i and j either bi pj or bj pi: Show that it is possible to specify an order in which the books are printed (and then bound) so that once the rst book is printed the binding machine will be kept busy until all the books are bound. As an example, nd a schedule for four books with printing time and binding time given as an ordered pair. (The rst coordinate is the printing time and the second coordinate is the binding time.) D = f(2, 3), (3, 5), (4, 1), (3, 3)g.
3.De ne an edge from i to j if bi pj ; where 1 i; j 4 and i 6= j. The directed Hamiltonian path in this directed graph gives the answer.
5.A bank plans to use special data lines to connect each of its branch o ces with the main o ce. The data line from a branch o ce need not be connected directly to the main o ce. A branch o ce may be connected indirectly to the main o ce by connecting to another branch o ce that is connected (directly or indirectly) to the main o ce. Every branch must be connected to the main o ce by some route. The distances between pairs of o ces are as follows:

|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
X |
160 |
270 |
75 |
70 |
190 |
|
|
2 |
160 |
X |
310 |
80 |
210 |
50 |
|
|
3 |
270 |
310 |
X |
175 |
120 |
215 |
|
|
4 |
75 |
80 |
175 |
X |
150 |
240 |
|
|
5 |
70 |
210 |
120 |
150 |
X |
100 |
|
|
6 |
190 |
50 |
215 |
240 |
100 |
X |
|
|
|
|
|
|
|
|
|
|
Determine which pairs of o ces should be connected by data lines so as to connect every branch o ce (directly or indirectly) to the main o ce with a minimum total cost. Repeat the procedure if there must be a data link between branches 2 and 5. Repeat the procedure if branches 1 and 4 cannot be connected by a data line.
5. (1,5,70), (1,4,75), (2,6,50), (2,4,80), (3,5,120) is a MCST. It is unique.
(1,4,75), (1,5,7), (2,6,50), (2,5,210), (3,5,120) is a MCST subject to the constraint.
(1,5,70), (2,6,50), (6,5,100), (3,5,120), (2,4,80) is a MCST subject to the constraint.
7.Use Fleury's algorithm to nd a Eulerian circuit in each of the following graphs given by the following adjacency list representation::
|
|
|
|
|
|
|
|
|
|
|
|
Adjacency Lists |
|
|
||
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
4 |
6 |
|
|
|
|
|
Adjacency Lists |
|
2 |
|
1 |
10 |
3 |
5 |
|
|
|||||
1 |
|
2 |
3 |
4 |
5 |
6 |
7 |
3 |
|
1 |
2 |
4 |
5 |
|
|
|
2 |
|
3 |
4 |
5 |
6 |
7 |
1 |
4 |
|
1 |
3 |
6 |
7 |
5 |
8 |
|
3 |
|
4 |
5 |
6 |
7 |
1 |
2 |
5 |
|
2 |
3 |
4 |
9 |
10 |
8 |
|
4 |
|
5 |
6 |
7 |
1 |
2 |
3 |
6 |
|
1 |
4 |
7 |
11 |
|
|
|
5 |
|
6 |
7 |
1 |
2 |
3 |
4 |
7 |
|
4 |
6 |
8 |
11 |
|
|
|
6 |
|
7 |
1 |
2 |
3 |
4 |
5 |
8 |
|
4 |
5 |
7 |
9 |
|
|
|
7 |
|
1 |
2 |
3 |
4 |
5 |
6 |
9 |
|
5 |
8 |
10 |
11 |
|
|
|
|
|
|
|
|
|
|
|
10 |
|
2 |
5 |
9 |
11 |
|
|
|
|
|
|
|
|
|
|
|
11 |
|
6 |
7 |
9 |
10 |
|
|
|
Fleury's Algorithm is as follows:
(a)Choose an arbitrary vertex v and set W = v.
(b)Suppose that the trail Wi = v ; v1 ; : : : ; vi has been chosen. Then, choose edge ei+1 from E fe1; e2; : : : ; eig in such a way that
(i)ei+1 is incident to vi
(ii)Unless there is no alternative, the removal of the edge
ei+1 does not disconnect the graph remaining after isolated vertices are removed.
