1. Основные типы и виды дифференциальных уравнений в частных производных.

Ранее рассматривались обыкновенные дифференциальные уравнения. Их решения зависят лишь от одной переменной: ,и т. д. Во многих практических задачах искомые функции зависят от нескольких переменных, и описывающие такие задачи уравнения могут содержать частные производные искомых функций. Они называютсяуравнениями с частными производными.

К решению дифференциальных уравнений с частными производными приводят, например, многие задачи механики сплошных сред. Здесь в качестве искомых функций обычно служат плотность, температура, напряжение и др., аргументами которых являются координаты рассматриваемой точки пространства, а также время.

Полная математическая постановка задачи наряду с дифференциальными уравнениями содержит также некоторые дополнительные условия. Если решение ищется в ограниченной области, то задаются условия на ее границе, называемые граничными (краевыми) условиями. Такие задачи называются краевыми задачами для уравнений с частными производными.

Если одной из независимых переменных в рассматриваемой задаче является время t, то задаются некоторые условия (например, значения искомых параметров) в начальный момент, называемые начальными условиями. Задача, которая состоит в решении уравнения при заданных начальных условиях, называется задачей Коши для уравнения с частными производными. При этом задача решается в неограниченном пространстве и граничные условия не задаются.

Задачи, при формулировке которых ставятся граничные и начальные условия, называются нестационарными (или смешанными) краевыми задачами. Получающиеся при этом решения меняются с течением времени.

Таким образом, математические модели физических и иных процессов описываются с помощью дифференциальных уравнений в частных производных. Аргументами функций этих уравнений являются пространственные координаты и время.

Уравнения первого порядка.Уравнения первого порядка называются также уравнениями переноса. Это объясняется тем, что такие уравнения описывают процессы переноса частиц в средах, распространения возмущений и т. п.

Его решение представляет интерес не только с практической точки зрения; в еще большей степени это уравнение полезно при разработке и исследовании разностных схем.

Будем считать, что искомая функция зависит от времении одной пространственной переменной х. Тогда линейное уравнение переноса может быть записано в виде

.

Здесь ‑ скорость переноса.

Уравнения второго порядка.Линейным уравнением в частных производных второго порядка называется соотношение между функциейилии ее частными производными вида.

(1)

Если переменная функция зависит оти, то уравнение может быть записано следующим образом:

(2)

В случае если , то уравнения 1-2 называются однородными, иначе ‑ неоднородными.

Если , то уравнение (2) относится к классу эллиптических уравнений;

если , то ‑ это гиперболическое уравнение;

если ‑ параболическое уравнение.

Когда не имеет постоянного знака, получается уравнение смешанного типа.

К классическим эллиптическим уравнениям относятся:

- уравнение Лапласа , которое используется для описания магнитных и стационарных тепловых полей;

- уравнение Пуассона , которое применяется в электростатике, теории упругости и других науках;

- уравнение Гельмголъца , описывающее установившиеся колебательные процессы.

Оператор Лапласа:

в одномерном случае ;

в двумерном случае ;

в трехмерном случае .

Среди гиперболических уравнений можно выделить:

Волновые уравнения:

одномерное , которое описывает вынужденные колебания струны;

двумерное , которое описывает колебания мембраны.

Телеграфное уравнение , которое описывает изменение потенциалав линиях электропередачи. Здесь- коэффициент самоиндукции, емкость, сопротивление, характеристика потерь на единицу длины линии.

К классическим параболическим уравнениям относится уравнение теплопроводности .

Для нахождения единственного решения дифференциального уравнения в частных производных необходимо задать начальные и граничные условия. Начальными условиями принято называть условия, заданные в начальный момент времени . Граничные условия задаются при различных значениях пространственных переменных. Для эллиптических уравнений задаются только граничные условия, которые можно разделить на три класса:

- условие Дирихле - в этом случае на границе области Г, в которой ищется решение, задана некая непрерывная функция. В одномерном случае это условие принимает вид:игде- интервал, на котором ищется решение одномерной задачи;

- условие Неймана - в этом случае на границе области Г задана производная по направлениювнешней нормали;

- смешанное условие .

Для параболических уравнений, кроме граничных условий, необходимо определить одно начальное, которое может быть таким: .

В случае гиперболических уравнений начальные условия могут быть следующими и.

Решение ряда дифференциальных уравнений в частных производных может быть получено аналитически. Одним из наиболее часто используемых методов является метод разделения переменных (метод Фурье). Рассмотрим этот метод подробнее.

О методах решения дифференциальных уравнений в частных производных.

Решение простейших задач для уравнений с частными производными в ряде случаев может быть проведено аналитическими методами, рассматриваемыми в соответствующих разделах математики. Это относится в основном к некоторым уравнениям первого порядка, а также к уравнениям второго порядка с постоянными коэффициентами. Аналитические методы полезны не только тем, что дают возможность получать общие решения, которые могут быть использованы многократно. Они имеют также огромное значение для построения численных методов. Проверка разностных схем на известных решениях простейших уравнений позволяет оценить эти схемы, выяснить их сильные и слабые стороны.

Среди численных методовшироко распространенными являются разностные методы. Они основаны на введении некоторой разностной сетки в рассматриваемой области. Значения производных, начальные и граничные условия выражаются через значения функций в узлах сетки, в результате чего получается система алгебраических уравнений, называемая разностной схемой. Решая эту систему уравнений, можно найти в узлах сетки значения сеточных функций, которые приближенно считаются равными значениям искомых функций.

Приведенные уравнения называются уравнениями математической физики. К их решению сводятся многие прикладные задачи. Прежде чем переходить к обсуждению численных методов решения указанных уравнений, рассмотрим основные вопросы построения разностных схем.

2. Введение в сеточные методы, понятия сетка, шаблон, слой.

О построении разностных схем. Как уже отмечалось, построение разностных схем решения уравнений с частными производными основано на введении сетки в рассматриваемом пространстве. Узлы сетки являются расчетными точками.

Пример простейшей прямоугольной области G(x, у)с границей Г в двумерном случае показан на рис 1,а. Стороны прямоугольника,делятся на элементарные отрезки точками, и, . Через эти точки проводятся два семейства координатных прямых,образующих сетку с прямоугольной ячейкой. Любой узел этой сетки, номер которого (), определяется координатами ().

аб

Рис. 1. Прямоугольная сетка (а), элемент трехмерной сетки (б)

Узлы сетки, лежащие на границе Г области G, называются граничными узлами. Все остальные узлы ‑ внутренними.

Аналогично вводятся сетки для многомерных областей. На рис. 1,бпоказан элемент сетки в виде прямоугольного параллелепипеда для трехмерной области.

Шаблон– комбинация используемых узлов

Поскольку начальные и граничные условия при постановке задач формулируются на границе расчетной области, то их можно считать заданными в граничных узлах сетки. Иногда граничные точки области не являются узлами сетки, что имеет место для областей сложной формы. Тогда либо вводят дополнительные узлы на пересечении координатных линий с границей, либо границу приближенно заменяют ломаной, проходящей через близкие к границе узлы. На эту ломаную переносятся граничные условия.

Рис. 2.

В ряде случаев сложные криволинейные области с помощью перехода к новым независимым переменным удается свести к простейшему виду. Например, четырехугольную область G, изображенную на рис. 2, можно привести к единичному квадратуG'путем введения новых переменных £, ц вместо #, у с помощью соотношений

К новым переменным нужно преобразовать уравнения, а также начальные и граничные условия. В области G'можно ввести прямоугольную сетку, при этом в областиGей будет соответствовать сетка с неравномерно расположенными узлами и криволинейными ячейками,

В дальнейшем при построении разностных схем мы для простоты будем использовать прямоугольные сетки (или с ячейками в виде прямоугольных параллелепипедов в трехмерном случае), а уравнения будем записывать в декартовых координатах (). На практике приходится решать задачи в различных криволинейных системах координат: полярной, цилиндрической, сферической н др. Например, если расчетную область удобно задать в полярных координатах (), то в ней сетка вводится с шагамиисоответственно по радиус-вектору и полярному углу.

Иногда и в простой расчетной области вводят неравномерную сетку. В частности, в ряде случаев необходимо проводить сгущение узлов для более точного расчета в некоторых частях рассматриваемой области. При этом области сгущения узлов либо известны заранее, либо определяются в процессе решения задачи (например, в зависимости от градиентов искомых функций).

Для построения разностной схемы, как и в случае обыкновенных дифференциальных уравнений, частные производные в уравнении заменяются конечно-разностными соотношениями по некоторому шаблону (см. гл. 3, § 1). При этом точные значения искомой функции Uзаменяются значениями сеточной функции и в узлах разностной сетки.

В качестве примера построим некоторые разностные схемы для решения уравнения теплопроводности при заданных начальных и граничных условиях. Запишем смешанную краевую задачу в виде

,(6)

где ‑ начальное распределение температурыU(приt= 0);‑ распределение температуры на концах рассматриваемого отрезка (х= 0, 1) в любой момент времениt. Заметим, что начальные и граничные условия должны быть согласованы, т. е.,.

Введем равномерную прямоугольную сетку с помощью координатных линий , и, ,и‑ соответственно шаги сетки по направлениямхиt. Значения функции в узлах сетки обозначим. Эти значения заменим соответствующими значениями сеточной функциикоторые удовлетворяют разностной схеме.

Заменяя в исходном уравнении (6) частные производные искомой функции с помощью отношений конечных разностей, получаем разностную схему

(7)

В записи этой схемы для каждого узла использован шаблон, изображенный на рис. 2, а.

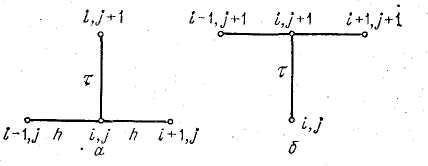
рис. 3

Для одного и того же уравнения можно построить различные разностные схемы. В частности, если воспользоваться шаблоном, изображенным на рис. 2, б, то вместо (7) получим разностную схему

(8)

И в том и другом случае получается система алгебраических уравнений для определения значений сеточной функции во внутренних узлах. Значения в граничных узлах находятся из граничных условий

(9)

Совокупность узлов при t= const, т. е. при фиксированном значении, называетсяслоем. Схема (7) позволяет последовательно находить значения,на-м слое через соответствующие значенияна-м слое. Такие схемы называютсяявными.

Для начала счета при j= 1 необходимо решение на начальном слое. Оно определяется начальным условием

(10)

В отличие от явной схемы каждое разностное уравнение (8) содержит на каждом новом слое значения неизвестных в трех точках, поэтому нельзя сразу определить эти значения через известное решение на предыдущем слое. Такие схемы называются неявными. При этом разностная схема (8) состоит из линейных трехточечных уравнений, т. е. каждое уравнение содержит неизвестную функцию в трех точках данного слоя. Такие системы линейных уравнений с трехдиагональной матрицей могут быть решены методом прогонкb, в результате чего будут найдены значения сеточной функции в узлах.

Заметим, что в рассмотренном примере мы получаем двухслойные схемы, когда в каждое разностное уравнение входят значения функции из двух слоев ‑ нижнего, на котором решение уже найдено, и верхнего, в узлах которого решение ищется.

С помощью рассматриваемого способа построения разностных схем, когда входящие в уравнение отдельные частные производные заменяются конечно-разностными соотношениями для сеточной функции (или сеточными выражениями), могут быть созданы многослойные схемы, а также схемы высоких порядков точности.

Уравнение Лапласа.Многие стационарные физические задачи (исследования потенциальных течений жидкости, определение формы нагруженной мембраны, задачи теплопроводности и диффузии в стационарных случаях и др.) сводятся к решению уравненияПуассонавида

1

Если , то это уравнение называется уравнениемЛапласа. Для простоты будем рассматривать двумерное уравнение Лапласа

2

Решение этого уравнения будем искать для некоторой ограниченной области Gизменения независимых переменныхх, у. Границей областиGявляется замкнутая линияL. Для полной формулировки краевой задачи кроме уравнения Лапласа нужно задать граничное условие на границеL. Примем его в виде

3

Задача, состоящая в решении уравнения Лапласа (или Пуассона) при заданных значениях искомой функции на границе расчетной области, называется задачей Дирихле.

Одним из способов решения стационарных эллиптических задач, в том числе и краевой задачи, является их сведение к решению некоторой фиктивной нестационарной задачи (гиперболической или параболической), найденное решение которой при достаточно больших значениях tблизко к решению исходной задачи. Такой способ решения называетсяметодом установления.

Поскольку решение U (х, у)нашего уравнения (2) не зависит от времени, то можно в это уравнение добавить равный нулю (при точном решении) член. Тогда уравнение (2) примет вид

4

Это ‑ известное нам уравнение теплопроводности, для которого уже строились разностные схемы. Остается только задать начальное условие. Его можно принять практически в произвольном виде, согласованном с граничными условиями. Положим

5

Граничное условие (3) при этом остается стационарным, т. е. не зависящим от времени.

Процесс численного решения уравнения (4) с условиями (3), (5) состоит в переходе при от произвольного значения (5) к искомому стационарному решению. Счет ведется до выхода решения на стационарный режим. Естественно, ограничиваются решением при некотором достаточно большом, если искомые значения на двух последовательных слоях совпадают с заданной степенью точности.

Метод установления фактически представляет итерационный процесс решения задачи, причем на каждой итерации значения искомой функции получаются путем численного решения некоторой вспомогательной задачи.

Для решения задачи Дирихле можно также построить разностную схему путем аппроксимации уравнения (2). Введем в прямоугольной области G сетку с помощью координатных прямых х= const и у = const. Примем для простоты значения шагов по переменнымхиуравнымиh(предполагается, что стороны области G соизмеримы). Значения функцииUв узлахзаменим значениями сеточной функции. Тогда, аппроксимируя в уравнении (2) вторые производные с помощью отношений конечных разностей, получим разностное уравнение (шаблон изображен на рис.):

(6)

Данное уравнение можно представить в виде системы линейных алгебраических уравнений относительно значений сеточной функции в узлах. Эту систему можно записать в виде

(7)

Значения сеточной функции в узлах, расположенных на границе расчетной области, могут быть найдены из граничного условия (3):

В теории разностных схем доказывается, что решение построенной разностной задачи существует, а сама схема устойчива.

Каждое уравнение системы (7) (за исключением тех, которые соответствуют узлам, расположенным вблизи границ) содержит пять неизвестных. Одним из наиболее распространенных методов решения этой системы линейных уравнений является итерационный метод. Каждое из уравнений записываем в виде, разрешенном относительно значения в центральном узле (см. рис.):

Итерационный процесс контролируется максимальным отклонением М значений сеточной функции в узлах для двух последовательных итераций. Если его величина достигнет некоторого заданного малого числа , итерации прекращаются.

Решение уравнения Лапласа в Mathcad. Для решения уравнений Лапласа и Пуассона вMathcadпредусмотрены встроенные функцииrelaxиmultigrid.

3. Решение дифференциальных уравнений с частными производными методом конечных разностей.

4. Решение эллиптических, параболических и гиперболических уравнений.

5. Нестационарные задачи.

6. Построение явной и неявной разностных схем для одномерного уравнения теплопроводности.

7. Вопросы аппроксимации, устойчивости и сходимости.

8. Метод прогонки.

9. Аппроксимация дифференциальных уравнений в частных производных системой обыкновенных дифференциальных уравнений (метод прямых).

10. Стационарные задачи, разностные схемы, счет на установление.

11. Вариационно-разностные методы.

12. Метод конечных элементов.