35

Лекция .

1. Решение систем нелинейных уравнений методами итераций и Ньютона-Рафсона.

2. Квадратурные формулы: методы прямоугольников, трапеций и Симпсона. Погрешности методов.

3. Интегрирование с автоматическим выбором шага интегрирования.

4. Вычисление кратных интегралов.

5. Вычисление определенного интеграла методом Монте-Карло.

1. Решение систем нелинейных уравнений методами итераций и Ньютона-Рафсона.

Ранее были рассмотрены методы решения систем линейных алгебраических уравнений. Для решения СЛАУ есть прямые методы решения, а для систем нелинейных уравнений не существует прямых методов решения. Для решения используются итерационные методы. Рассмотрим 2 метода.

Метод итераций.

Исходная система имеет вид

Перепишем эту систему в виде

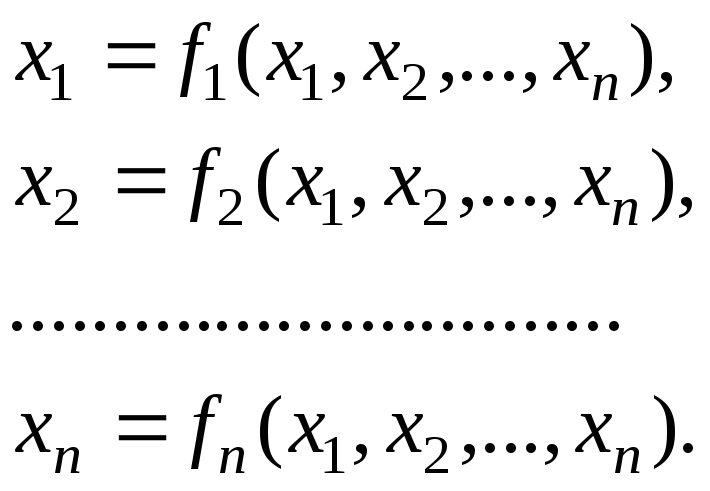
Алгоритм решения этой системы методом простой итерации напоминает метод Гаусса-Зейделя, используемый для решения СЛАУ.

В результате первой итерации получим значения неизвестных

,

а выражения для нахождения неизвестных на следующей итерации будут иметь вид

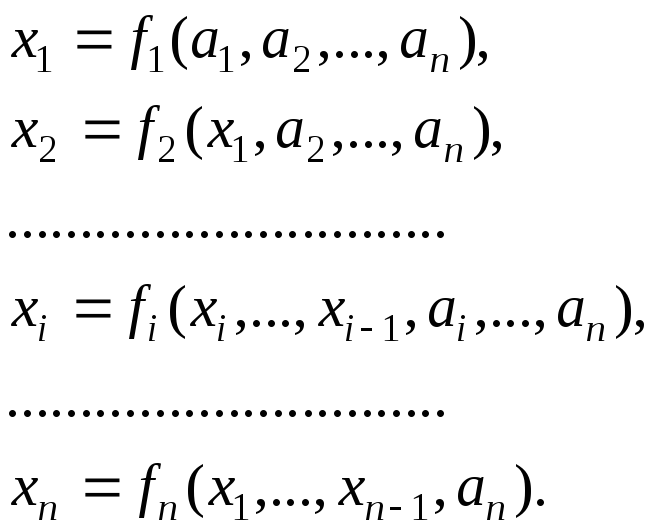
Итерационный процесс продолжается до тех пор, пока изменения всех неизвестных в двух последовательных итерациях не станут малыми, т.е. абсолютные величины их разностей не станут меньшими заданного малого числа.

При использовании метода итераций для решения системы нелинейных уравнений необходимо учитывать особенность: достаточно близки к истинному решению, иначе итерационный процесс может не сойтись.

Метод Ньютона.

Метод Ньютона обладает более быстрой сходимостью, чем метод простой итерации. Метод Ньютона для одного нелинейного уравнения заключался в записи уравнения касательной к кривой .

В основе метода Ньютона для системы нелинейных уравнений лежит использование разложения функций

в ряд Тейлора, причем члены, содержащие вторые (и более высоких порядков) производные, отбрасываются.

Допустим приближенные значения неизвестных (полученные на предыдущей итерации) равны соответственно .

Задача состоит в нахождении поправок к этим значениям .

Тогда решение запишется в виде

,, ….

Проведем разложение левых частей исходной системы в ряд Тейлора, ограничиваясь лишь линейными членами относительно приращений. Получим:

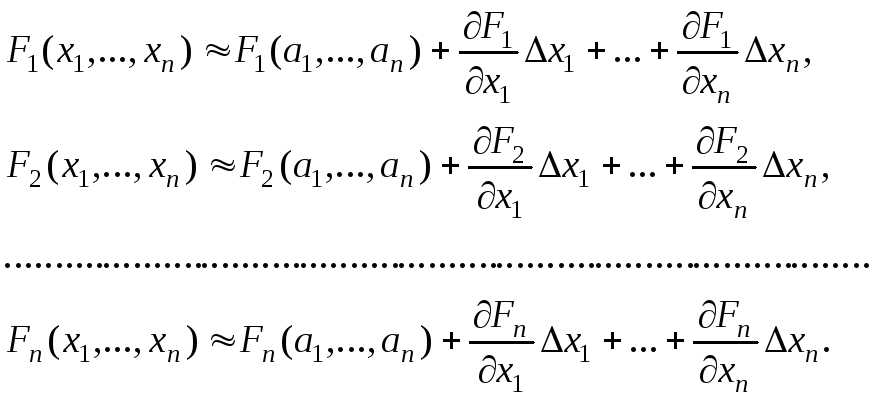
Поскольку левые части исходной системы равны нулю, то можем приравнять нулю и правые части последней системы, тогда получим

(*)

В этой системе значения и их производные вычисляются при

.

Определителем последней системы является якобиан (матрица Якоби)

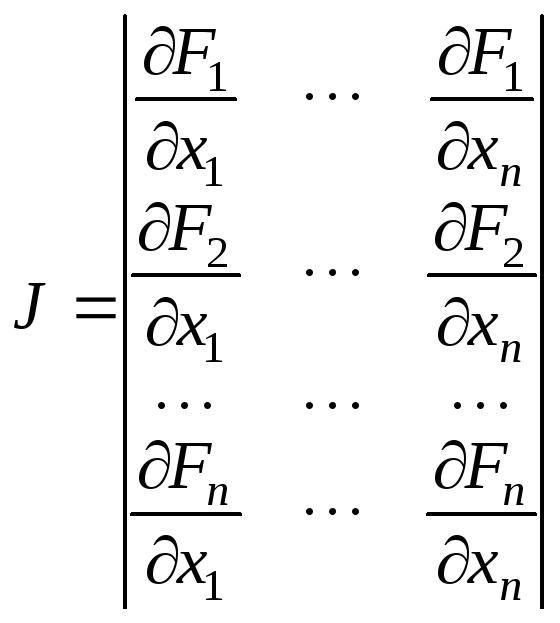
Для существования единственного решения системы (*) якобиан должен быть отличным от нуля на каждой итерации. Счет прекращается, если все приращения становятся малыми по абсолютной величине: .

В методе Ньютона также важен удачный выбор начального приближения для обеспечения хорошей сходимости. Сходимость ухудшается с увеличением числа уравнений системы.

2. Квадратурные формулы: методы прямоугольников, трапеций и Симпсона. Погрешности методов.

Численное вычисление определенного интеграла называют механической квадратурой, а формулы, соответствующие тому или иному численному методу приближенного интегрирования, называют квадратурными.Подобное название связано с геометрическим смыслом определенного интеграла:

значение определенного интеграла равно площади квадрата, которая в свою очередь совпадает с площадью криволинейной трапеции с основаниямии.

Метод прямоугольников.

Интегрирование по методу прямоугольниковзаключается в том, что интервал интегрированияделится точкаминаравных частей (рис.), причем

,,

длина каждой части составляет

,

и тогда

.

Из каждой точки . проведем перпендикуляр до пересечения с кривой, а затем заменим кривую подынтегральной функции ломаной линией, отрезки которой параллельны оси абсцисс.

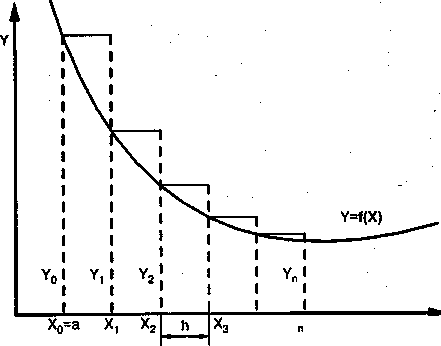
Графическая интерпретация метода левых прямоугольников.

Площадь полученной ступенчатой фигуры можно найти как сумму площадей прямоугольников, стороны которых равны и. Следовательно, площадь отдельного прямоугольника составит

,

тогда

Следовательно, формула вычисления определенного интеграла по методу прямоугольников имеет вид:

Эту формулу называют еще квадратурной формулой левых прямоугольников. Поясним почему. Рассмотрим другую геометрическую интерпретацию метода прямоугольников, изображенную на рис.

Графическая интерпретация метода правых прямоугольников.

В этом случае площадь ступенчатой фигуры будем вычислять так:

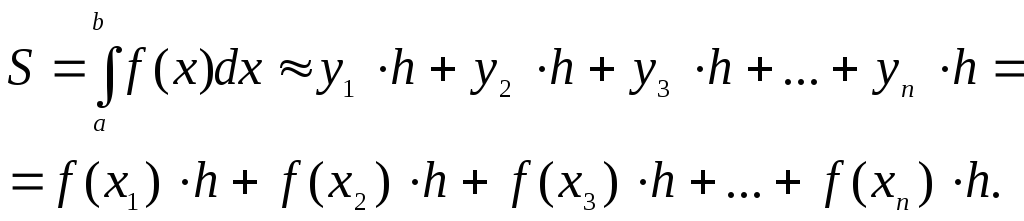
Из чего вытекает квадратурная формула правых прямоугольников:

Рис. содержит еще один пример геометрической интерпретации интегрирования по методу прямоугольников.

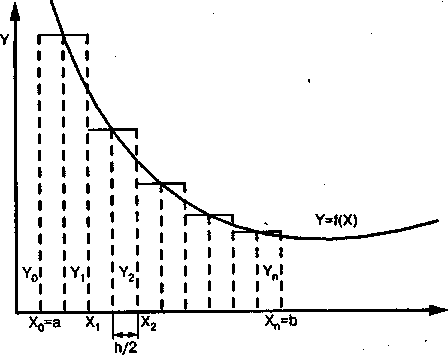
Графическая интерпретация метода средних прямоугольников.

Идея этого метода заключается в том, что значение функции вычисляется в точке, расположенной в середине отрезка , то есть

.

Из чего вытекает квадратурная формула средних прямоугольников:

Эта формула имеет большую точность по сравнению с двумя предыдущими, поэтому именно ее применяют чаще всего и называют формулой прямоугольников.

Метод трапеций.

Для интегрирования методом трапеций участок интегрирования делится точками наравных частей. Если провести ординаты во всех точках деления и заменить каждую из полученных криволинейных трапеций прямолинейной (рис.), то приближенное значение интеграла будет равно сумме площадей прямолинейных трапеций.

Геометрическая интерпретация метода трапеций

Площадь отдельной трапеции составляет:

.

Следовательно, площадь искомой фигуры вычисляют по формуле:

Таким образом, получена квадратурная формула трапецийдля численного интегрирования:

Метод Симпсона.

Пусть ‑ четное число, а(где) ‑ значения функциидля равноотстоящих точекс шагом.

На паре соседних участков (рис.) кривая заменяется параболой, коэффициенты которой подобраны так, что она проходит через точки.

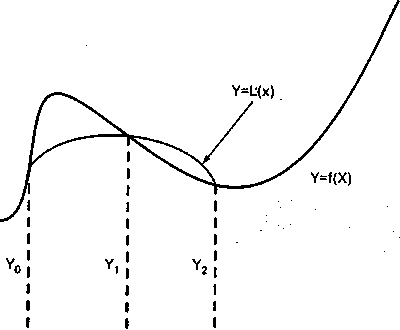
Геометрическая интерпретация интегрирования по методу Симпсона

Площадь криволинейной трапеции, ограниченной сверху параболой, составит:

.

Суммируя площади всех криволинейных трапеций, получим:

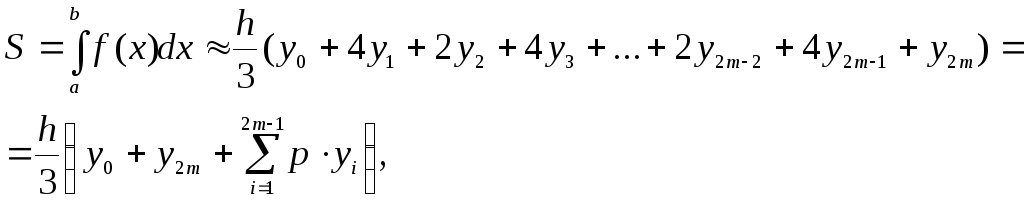
где .

Следовательно, формула Симпсонадля численного интегрирования имеет вид:

.

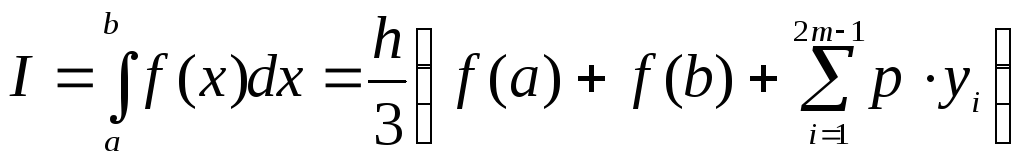3. Погрешности методов. Интегрирование с автоматическим выбором шага интегрирования.

При одном и том же числе точек формула Симпсона в большинстве случаев намного точнее, чем формулы прямоугольников и трапеций.

Точность интегрирования е по методу прямоугольников с постоянным шагом связана с величиной шага следующим образом:

.

При интегрировании методом трапеций это соотношение имеет вид:

Метод Симпсона обеспечивает точность вычислений:

.

Ошибка в выборе величины шага интегрирования либо не обеспечит нужной точности, либо приведет к необоснованным затратам машинного времени. Заданную точность при минимальных затратах времени обеспечивают алгоритмы интегрирования с автоматическим выбором величины шага. Блок-схема вычисления интеграла с заданной точностью приведена на рис. Здесь ‑ функция, вычисляющая значение интеграла на участке отдолюбым из приведенных ранее методов с заданной точностью,‑ число разбиений подынтегральной функции на заданном участке интегрирования.

4. Вычисление кратных интегралов.

Рассмотрим на примере двойного интеграла

.

Одним из способов вычисления этого интеграла является метод ячеек. Рассмотрим случай, когда областью интегрирования является прямоугольник:.

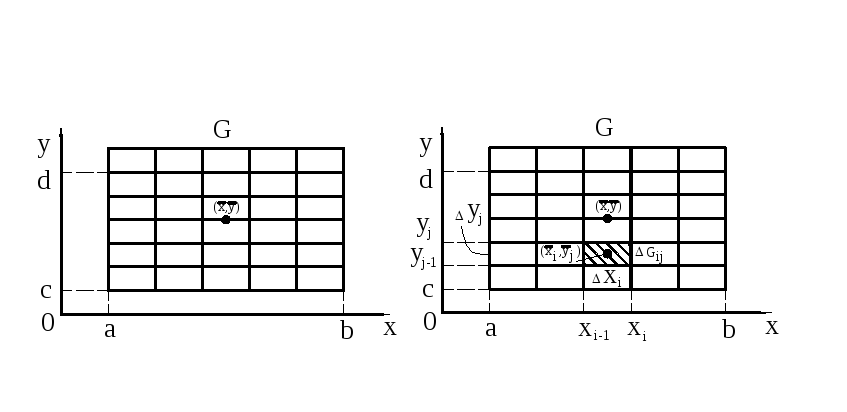
По теореме о среднем найдем среднее значение функции :

,. (*)

Будем считать, что среднее значение приближенно равно значению функции в центре прямоугольника, т.е. .

Тогда из (*) получим выражение для приближенного вычисления двойного интеграла:

,

,.

Точность этой формулы можно повысить, если разбить область на прямоугольные ячейки:

, .

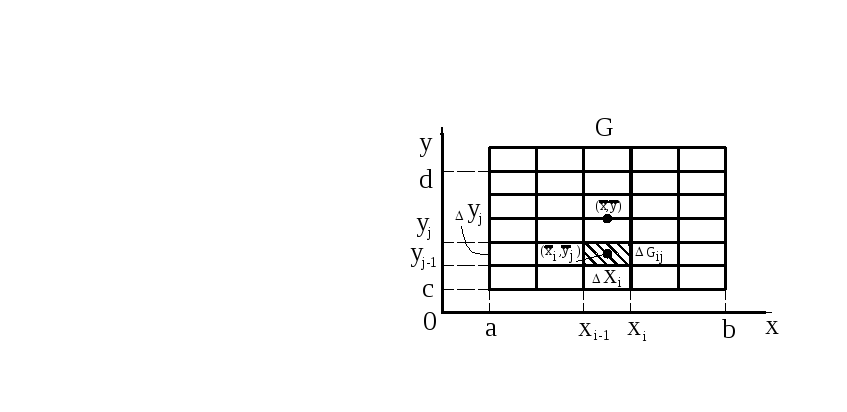
Для каждой из ячеек получаем

.

Значение двойного интеграла определяется как сумма выражений по всем ячейкам:

.

В правой части стоит интегральная сумма и при неограниченном уменьшении периметров ячеек (или стягивании их в точки) эта сумма стремится к значению интеграла для любой непрерывной функции .

Если область интегрирования непрямоугольная, то в ряде случаев ее целесообразно привести к прямоугольному виду путем замены соответствующих переменных.

Например пусть область задана в виде криволинейного четырехугольника: . Данную область можно привести к прямоугольному виду с помощью замены

,.

Другим довольно распространенным методом вычисления кратных интегралов является их сведение к последовательному вычислению определенных интегралов. Для прямоугольной области можно записать в виде

,.

Если область интегрирования имеет более сложную форму, то она либо приводится к прямоугольному виду с помощью замены переменных, либо разбивается на простые элементы.

Для вычисления кратных интегралов используется также метод замены подынтегральной функции многомерным интерполяционным многочленом. Вычисление коэффициентов этих многочленов для простых областей не вызывает затруднений.

Существует ряд других численных методов вычисления кратных интегралов. Среди них особое место занимает метод статистических испытаний (метод Монте-Карло).

5. Вычисление определенного интеграла методом Монте-Карло.

Во многих задачах исходные данные содержат случайный характер, поэтому для их решения должен применяться статистико-вероятностный подход. На таком подходе пострен метод статистических испытаний (метод Монте-Карло).

Метод Монте-Карло состоит в том, что рассматривается некоторая случайная величина , математическое ожидание которой равно искомой величине:

.

Проводится серия независимых испытаний, в результате которых генерируется последовательностьслучайных чисел, и по совокупности этих значений приближенно определяется искомая величина

,

.

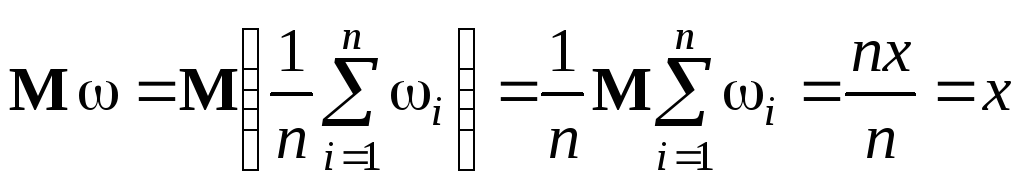Пусть ‑ равномерно распределенная на отрезке [0, 1] случайная величина, т.е. ее плотность распределения задается условием

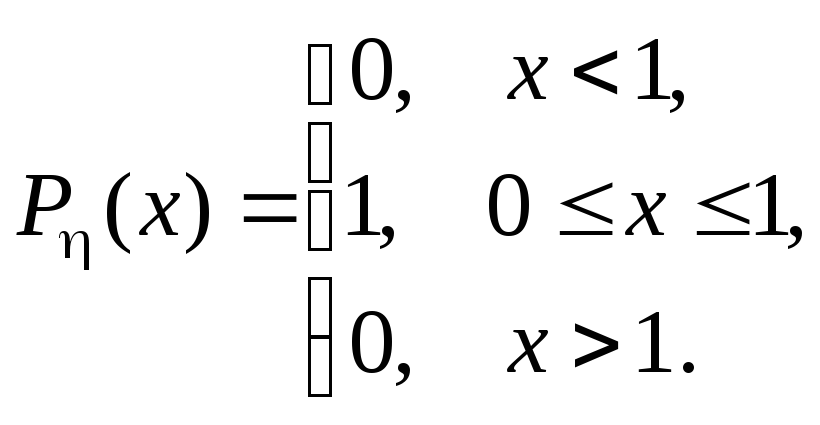
Тогда любая функция также будет случайной величиной, и ее математическое ожидание равно

.

Следовательно, читая это неравенство в обратном порядке, приходим к выводу, что интеграл может быть вычислен как математическое ожидание некоторой случайной величины, которая определяется независимыми реализациямислучайной величиныс равномерным законом распределения:

.

Аналогично можно определить и кратные интегралы. Для двойного интеграла получим

,

где поверхность :, а‑ независимые реализации случайных величин, равномерно распределенных на отрезке [0, 1].

Раздел. Численное решение

обыкновенных дифференциальных уравнений