Matematika (1)

№2 Число А называется пределом функции у = f(х) при х, стремящимся к х₀, если для любого, даже сколь угодно малого положительного числа e, найдется такое положительное число d ( зависящее от e), что для всех х , не равных х₀ и удовлетворяющих условию

| х- х₀ | < d,

верно неравенство:

| f(x)– А | < e

Этот предел функции обозначается: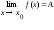

Число А называется пределом функции у = f (х) при х, стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа e, найдется такое положительное число S ( зависящее от e), что для всех х таких, что |х| > S, верно

неравенство: |f(x)–А|<e|

Этот предел функции обозначается:

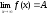
• №3 Теорема 1. Функция не может иметь более одного предела.

• Теорема 2. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е.

• 

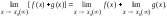
• Теорема 3. Предел произведения конечного числа функций равен произведению пределов этих функций, т.е

• .

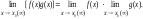
• Следствие.1. Постоянный множитель можно выносить за знак предела, т.е.

• 

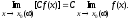
• Следствие 2. Предел степени равен степени предела, т.е.

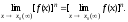
• Теорема 4. Предел частного двух функций равен частному пределов этих функций, при условии, что предел делителя не равен нулю, т.е.

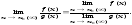
№4

• Определение 1. Функция ¦(х) называется непрерывной в точке х₀, если она удовлетворяет следующим трем условиям:

• 1) определена в точке х₀ (т.е. существует ¦(х₀));

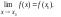
• 2) имеет конечный предел функции при х ® х₀;

• 3) этот предел равен значению функции в этой точке , т.е.

• Определение 2. Функция у =¦(х) называется непрерывной в точке х₀, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:

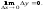
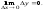
• Теорема. Сумма, разность, произведение и частное двух функций непрерывных в одной и той же точке а, есть функция непрерывная в той же точке, причем в случае частного предполагается, что функция делитель не обращается в нуль при х = а. (Теорема остается верной для суммы и произведения любого конечного числа функций).

• Функция у = ¦(х) называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка.

• Доказано, что все элементарные функции непрерывны в области их определения.

№5

• Точка х₀, в которой функция ¦(х) не является непрерывной называется точкой разрыва.

• Точка х₀ называется точкой разрыва первого рода, если существуют конечные односторонние пределы функции слева или справа при х ® х₀, не равные друг другу, либо если они равны между собой, но не равны значению функции в точке х₀.

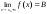
• Обозначим

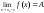
• а) , в этом случае функция имеет скачок

• б) ,но не равно значению функции в точке х₀ , имеем устранимый разрыв. Точка х₀ называется точкой разрыва второго рода, если хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует.

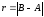
№6

• Производной функции у = ¦(х) называется предел отношения приращения функции Dу к приращению аргумента Dх при стремлении Dх к нулю.

• Если функция в точке х₀ имеет конечную производную, то функция называется дифференцируемой в этой точке.

• Функция дифференцируемая во всех точках промежутка Х, называется дифференцируемой на этом промежутке.

№7

• Теорема Ферма. Если дифференцируемая на промежутке функция y=f(x) достигает наибольшего или наименьшего значения во внутренней точке x₀ этого промежутка, то производная функции в этой точке равна нулю, т.е. f′(x₀)=0.

• Теорема Ролля. Пусть функция y=f(x) удовлетворяет следующим условиям:

непрерывна на [a,b];

дифференцируема на [a,b];

на концах отрезка принимает равные значения, т.е. f(a)= f(b).

Тогда внутри отрезка существует по крайней мере одна такая точка

ε ( a,b), в которой производная равна нулю (f′(ε)=0).

• Теорема Лагранжа. Пусть функция y=f(x) удовлетворяет следующим условиям:

непрерывна на [a,b];

дифференцируема на [a,b].

Тогда внутри отрезка существует по крайней мере одна такая точка

С( a,b), в которой производная равна частному от деления приращения функции к приращению аргумента на этом отрезке, т.е.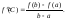

№13

• Совокупность всех первообразных для функции f (х) на промежутке Х называется неопределенным интегралом от функции f (х) и обозначается ò f (х) dx , где ò - знак интеграла, f (х) – подынтегральная функция, f (х) dx – подынтегральное выражение.

Производная от неопределенного интеграла равна подынтегральной функции, т.е. (ò f (х) dx) ¢= f (х).

Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е. d (ò f (х) dx) = f (х) dх.

Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.

ò dF(x) =F(x) + C.

Неопределенный интеграл от алгебраической суммы конечного числа функций равен такой же сумме неопределенных интегралов от этих функций, т.е. ò [f (х) + g (x)] dx =ò f (х) dx + ò g (х) dx.

Постоянный множитель можно выносить за знак неопределенного интеграла, т.е. ò a f (х) dx =a ò f (х) dx.

№15

Интегрирование методом разложения.

Этот метод основан на разложении подынтегральной функции на сумму функций, от каждой из которых первообразную можно найти с помощью таблицы или других методов.

Например ò (х³ + 3sinx – 8) dx = ò х³ dx + 3òsinx dx – 8òdx =< используя формулы из таблицы>= х⁴/4 - 3 cos x – 8 х + С.

Интегрирование методом замены переменных.

Интегрирование этим методом заключается в приведении данного интеграла к новому путем замены переменной интегрирования х на новую переменную z. Пусть х = g(z), тогда dx = g¢( z)dz. Поэтому

ò f(х) dx = ò f [g(z)] g¢( z)dz = Ф (z) +С = Ф [g^-1(х)] + С.

Интегрирование по частям.

Пусть u(x) и v(x) – две функции от х, имеющие непрерывные производные, тогда справедлива следующая формула:

ò udv = uv - ò vdu.

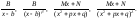
Интегрирование рациональной дроби

Задача интегрирования сводится к интегрированию простейших дробей следующих четырех типов:

Здесь, β=2, 3, …; λ=2, 3, …; B, M, N, b, p и q – некоторые вещественные числа, причем трехчлен x²+px+q не имеет вещественных корней, т.е. q-p²/4>0.

При этом справедлива следующая теорема: Всякая рациональная дробь интегрируема в элементарных функциях.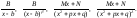

№17

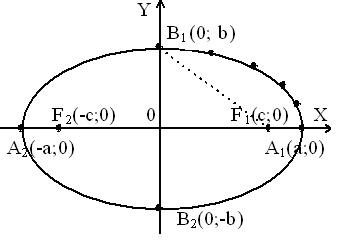
• Эллипсом называется геометрическое место точек на плоскости, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина равная 2а.

• F₁(c,0), F₂(-c,0) – фокусы эллипса. A₁(a,0),A₂(-a,0), B₁(0,b), B₂(0,-b) – вершины эллипса

№18

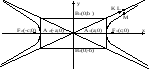
• Гиперболой называется геометрическое место точек на плоскости, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная равная

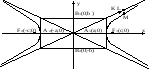
• Фокусы гиперболы обозначим через F₁ и F₂, а расстояние между ними - через 2с

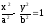
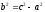
№19

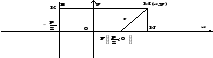
• Параболой называется геометрическое место точек на плоскости, каждая из которых равноудалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой (предполагается, что эта прямая не проходит через фокус).

• y²=2px - каноническое уравнение параболы

№22

или, в сокращенной записи А=( а_ij) i=1.. m; j=1.. n

Две матрицы А и В одного размера mхn называются равнымиесли они совпадают поэлементно,

т.е. а_ij =b_ij для всех i=1.. m; j=1.. n.

Классификация матриц

• Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца – матрицей (вектором)-столбцом.

• Квадратной матрицей n-го порядка называется матрица, у которой число строк равно числу столбцов и равно n.

• Элементы матрицы а_ij, у которых i = j называются диагональными элементами и образуют главную диагональ.

• Если все недиагональные элементы квадратной матрицы равны нулю, то она называется диагональной .

• Единичной, называется диагональная матрица, элементы которой равны единице.

• Симметрической называется квадратная матрица, у которой элементы, расположенные симметрично относительно главной диагонали,равны, т.е.

• Треугольная матрица – квадратная матрица, у которой все элементы, стоящие по одну из сторон главной диагонали, равны нулю

№23операции над матрицами

• Умножение матрицы на число.

• Произведением матрицы А на число λ называется матрица В=λА, элементы которой b_ij =λ а_ij для всех i=1… m; j=1… n.

• Сложение матриц.

• Суммой двух матриц А и В одинакового размера mxn называется матрица С=А+В, элементы которой с_ij =а_ij+ b_ij для всех i=1… m; j=1…n.

• Вычитание матриц.

• Разность двух матриц одинакового размера определяется через предыдущие операции: А – В = А + ( −1 )∙В.

• Умножение матриц.

• Умножение матриц А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц называется такая матрица , каждый элемент которой с_ij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В.

• Целой положительной степенью А^m квадратной матрицы А называется произведение m матриц А, т.е. А^m = А ∙А∙ …∙А

• Транспонирование матрицы.

• Транспонированием матрицы называется переход от матрицы А к А^т (или А'), в которой строки и столбцы поменялись местами с сохранением порядка. А^т – называется транспонированной относительно матрицы А.

№24

• Каждой квадратной матрице А, можно поставить в соответствие вычисленное по определенным правилам число, называемое определителем квадратной матрицы.

• Определителем матрицы первого порядка А=(а₁₁) или определителем первого порядка называется элемент а₁₁. Обозначается Δ₁ = а₁₁ или│А│= а₁₁.

• Определителем матрицы второго порядка или определителем второго порядка называется число, которое вычисляется по формуле: Δ₂ = │А│= а₁₁а₂₂ – а₁₂а₂₁ .

• Определителем матрицы третьего порядка

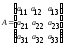
или определителем третьего порядка называется число, которое вычисляется по формуле:

Δ₃ = │А│= а₁₁а₂₂ а₃₃+а₁₂а₂₃а₃₁+а₂₁а₃₂а₁₃– а₃₁а₂₂а₁₃

– а₁₂а₂₁а₃₃ – а₃₂а₂₃а₁₁.

Свойства определителей

• 1.Если какая-либо строка (столбец) матрицы состоит из одних нулей, то её определитель равен нулю.

• 2.Если все элементы какой-либо строки (столбца) матрицы умножить на число λ, то её определитель умножится на это число λ.

• 3. При транспонировании матрицы её определитель не изменится.

• 4. При перестановке 2-х строк (столбцов) матрицы её определитель меняет знак на противоположный.

• 5. Если матрица содержит две одинаковые строки (столбца), то её определитель равен нулю.

• 6. Если элементы двух строк (столбцов) матрицы пропорциональны, то её определитель равен нулю.

• 7. Определитель матрицы не изменится, если к элементам любой строки (столбца) прибавить элементы другой строки (столбца), предварительно умноженной на любое число.

• 8. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна нулю.

9. Определитель произведения двух квадратных матриц равен произведению их определителей: │АВ│=│А││В│.

№25

• Матрица А^-1 называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица: А^-1∙А = А ∙А^-1 = Е.

• Если определитель матрицы отличен от нуля, то такая матрица называется невырожденной, или неособенной; в противном случае (при │А│=0 ) – вырожденной, или особенной .

1. Находим определитель исходной матрицы.

2.Если │А│=0, то матрица А вырожденная и обратной матрицы А^-1 не существует.

Если определитель матрицы А не равен нулю, то обратная матрица существует.

3. Находим А^T, транспонированную к А.

4. Находим алгебраические дополнения элементов транспонированной матрицы и составляем из них присоединенную матрицу . 5. Вычисляем обратную матрицу по формуле: 6. Проверяем правильность вычисления обратной матрицы, исходя из её определения А^-1∙А = А ∙А^-1 = Е.

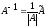
• №28

• В матрице размера m x n вычеркиванием каких-либо строк и столбцов можно выделить квадратные подматрицы k-го порядка, где k≤min(m; n). Определители таких подматриц называются минорами k-го порядка матрицы А.

• Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.

• Ранг матрицы А обозначается rang A или r(A).

• Из определения следует:

• 1) ранг матрицы размера m x n не превосходит меньшего из её размеров, т.е. r(A) ≤ min (m; n).

• 2) r(A)=0 тогда и только тогда, когда все элементы матрицы равны нулю, т.е. А=0.

• 3) Для квадратной матрицы n-го порядка r(A) = n тогда и только тогда, когда матрица А – невырожденная.

• В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются элементарные преобразования, сохраняющие ранг матрицы:

• 1) Отбрасывание нулевой строки (столбца).

• 2) Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.

• 3) Изменение порядка строк (столбцов) матрицы.

• 4) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

• 5) Транспонирование матрицы.

• Теорема. Ранг матрицы не изменится при элементарных преобразованиях матрицы.

№31

• Пусть число уравнений системы (1) равно числу переменных, т.е. m=n. Тогда матрица системы является квадратной, а её определитель Δ=│А│называется определителем системы.

• Предположим, что │А│не равен нулю, тогда существует обратная матрица А^-1.

• Умножая слева обе части матричного равенства на обратную матрицу А^-1 получим:

• А^-1 (АХ)= А^-1 В.

Решением системы уравнений методом обратной матрицы будет матрица-столбец:

Х= А^-1В.

(А^-1 А)Х =ЕХ =Х

• Теорема Крамера. Пусть Δ – определитель матрицы системы А, а Δ_j – определитель матрицы, полученный из матрицы заменой j-го столбца столбцом свободных членов. Тогда если Δ не равен нулю, то система имеет единственное решение, определённое по формулам Крамера:

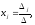
где j=1..n.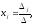

№33

• Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого или треугольного вида.

• Рассмотрим матрицу:

• эта матрица называется расширенной матрицей системы (1), так как в нее кроме матрицы системы А, дополнительно включен столбец свободных членов.

№26

• N-мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде Х=(х₁,х₂,…х_n) , где х_i – i-я компонента вектора Х.

• Два n-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е. Х=У, если x_i=y_i, i=1…n.