Matematika (1)

Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие приведённым выше свойствам, называется векторным пространством.

• Векторное пространство R, называется n-мерным, если в нем существует n линейно независимых векторов, а любые n+1 векторов уже являются зависимыми. Число n называется размерностью векторного пространство R и обозначается dim(R).

№29

Линейные операторы

• Определение. Если задан закон (правило), по которому каждому вектору x пространства ставится в соответствие единственный вектор y пространства

то говорят: что задан оператор (преобразование, отображение) A(x), действующий из в и

записывают y=A(x).

• Оператор называется линейным, если для любого вектора x и y пространства

и любого числа λ выполняются следующие соотношения: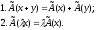

№37

• Пустъ А – множество, состоящее из конечного числа элементов a₁, a_2, a₃…a_n. Из различных элементов множества А можно образовывать группы. Если в каждую группу входит одно и то же число элементов m (m из n), то говорят, что они образуют соединения из n элементов пo m в каждом. Различают три вида соединений: размещения, сочетания и перестановки.

• Соединения, в каждое из которых входят все n элементов множества А и которые, следовательно, отличаются друг от друга только порядком элементов называются перестановками из n элементов. Число таких перестановок обозначается символом Р_n.

№35

Классическое определение вероятности основано на понятии равновозможности событий.

Равновозможность событий означает, что нет оснований предпочесть какое-либо одно из них другим.

Рассмотрим испытание, в результате которого может произойти событие A. Каждый исход, при котором осуществляется событие A, называется благоприятным событию A.

Вероятностью события A (обозначают P(A)) называется отношение числа исходов, благоприятных событию A (обозначают k), к числу всех исходов испытания – N т.е. P(A)= k/ N.

• Из классического определения вероятности вытекают следующие ее свойства:

• Вероятность любого события заключена между нулем и единицей.

• Вероятность достоверного события равна единице.

• Вероятность невозможного события равна нулю

№39, 40

• Теорема сложения. Если А и В несовместны, то Р(А + В) = Р(А) +Р(В)

Если и противоположные события, то

Теорема умножения. Если А и В независимые события, то

Р(АВ) = Р(А)Р(В).

Если А и В совместны, то теорема сложения принимает вид:

Р(А+В)=Р(А)+Р(В) - Р(АВ) .

№41

• Пусть событие А может наступить при условии реализации одной из гипотез Н₁, Н₂, ..., Н_n, образующих полную группу событий.

Тогда

• Формула (1) называется формулой полной вероятности.

№№42

• Предположим, что в результате испытания событие А произошло. Какова вероятность, что событие А произошло в результате реализации гипотезы Н_k , т.е. P(H_k/A) = ? (происходит переоценка вероятностей гипотез). Ответ дает формула Байеса:

№44

• Дисперсией D(X) случайной величины называется математическое ожидание квадрата ее отклонения от математического ожидания:

• D(X) = M[Х-M(X)]² или D(X) = M[X-a]² , где а = М(Х). Часто вместо дисперсии используют среднее квадратическое отклонение:

• Свойства дисперсии случайной величины.

• 1. Дисперсия постоянной величины равна нулю: D(С) = 0.

• 2. Постоянный множитель можно выносить за знак дисперсии, возводя его и квадрат : D(кХ) = к²D(X)

• 3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом математического ожидания D(X) = М(Х²)-[М(Х)]².

№46

• Дисперсией D(X) непрерывной случайной величины называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

• D(Х) = М[Х-a]², а=M(X).

№№46

• Справедливы формулы:

• µ₀=1;

• µ₁=0;

• µ₂= α₂- α²;

• µ₃= α₃- 3αα₂+2α³;

• µ₄=α₄ +6α²α₂-4αα₃-3α⁴.

• Величина называется коэффициентом асимметрии. Он

• характеризует «скошенность» распределения случайной величины по отношению к математическому ожиданию.

• Для симметричных распределений µ₃=0, поэтому коэффициент асимметрии равен нулю.

№47

Дискретная случайная величина X имеет биномиальный закон распределения, если она принимает значения 0,1, 2,…,m,….,n с вероятностями р(m) = Р(Х = m) = C_n^m р^m q^n-m, где 0 < p <1, q = 1─ р.

• Биномиальный закон распределения представляет собой закон распределения числа Х = m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.

Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по биномиальному закону, даются формулами

M(X) = np, D(X) = npq.

• Следствие. Математическое ожидание величины (m/n) в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью р, равно р, т.е. M(m/n) = р, D(m /n)=pq/n.

• Дискретная случайная величина X имеет закон распределения Пуассона, если она принимает значения 0,1 2,…,m,…,n с вероятностями р(m) = Р(Х=m) =е^─λ λ^m/m! , где λ = np.

Tеорема. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона. т.е. М(Х) = λ, D(X)= λ.

Распределение Пуассона ─ частный случай биномиального закона распределения для относительно больших n и относительно малых р.

• Равномерный закон распределения

Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [a, b], если её плотность вероятности постоянна на этом отрезке и равна нулю вне его, т.e.

• Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами а и s² , если её плотность вероятности имеет вид:

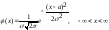
№48 Числовые характеристики системы двух случайных величин

Условным математическим ожиданием дискретной случайной величины Y при X=x (x- определенное возможное значение X) называют сумму произведений возможных значений Y на их условные вероятности:

• Для непрерывных величин:

• 

• где - условная плотность случайной величины Y при X=x.

Зависимые и независимые случайные величины

• Теорема. Для того, чтобы случайные величины X и Y были независимыми необходимо и достаточно, чтобы функция распределения системы (Х, У) была равна произведению функций распределения составляющих: F(x,y)= F₁(x)F₂(y)

• Ковариацией (или корреляционным моментом) называется математическое ожидание произведения отклонения этих величин от своих математических ожиданий: