12. Поиск экстремума функции нескольких переменных.

Как и в случае одной переменной, функция z = f (x,у) имеет узловые, определяющие структуру графика, точки.

Точка М₀ (х₀, у₀) называется точкой максимума (минимума) функции z = f (x,у) , если существует окрестность точки М такая, что для всех точек (х, у) из этой окрестности выполняется неравенство: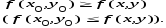

Теорема (необходимое условие экстремума). Пусть точка М₀ (х₀, у₀) – есть точка экстремума дифференцируемой функции z = f (x,у) . Тогда частные производные и в этой точке равны нулю.

13 Неопределенный интеграл, основные теоремы.

Функция F(х) называется первообразной функции f (х) на промежутке Х, если в каждой точке х этого промежутка F ¢(х) = f (х).

Например, F(х) = х²/2 является первообразной для функции f (х) = х, так как (х²/2)¢ = х.

Теорема. Если функция F(х) является первообразной функции f(х) на промежутке Х, то всякая другая первообразная для функции f(х) отличается от F(х) на постоянное слагаемое, т.е. может быть представлена в виде:

F(х) + С, где С – произвольная постоянная.

Совокупность всех первообразных для функции f (х) на промежутке Х называется неопределенным интегралом от функции f (х) и обозначается ò f (х) dx , где ò - знак интеграла, f (х) – подынтегральная функция, f (х) dx – подынтегральное выражение.

Свойства неопределенного интеграла:

1.Производная от неопр. интеграла равна подынтегральной функции, т.е. (ò f (х) dx) ¢= f (х).

2.Дифференциал неопр. инт-ла равен подынтегральному выражению, т.е. d (ò f (х) dx) = f (х) dх.

3.Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е. ò dF(x) =F(x) + C.

4.Неопр. интеграл от алгебраической суммы конечного числа функций равен такой же сумме неопределенных интегралов от этих функций, т.е. ò [f (х) + g (x)] dx =ò f (х) dx + ò g (х) dx.

5.Постоянный множитель можно выносить за знак неопр. инт-ла, т.е. ò a f (х) dx =a ò f (х) dx.

Таблица основных интегралов.

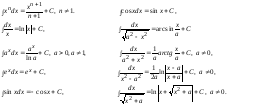
14. Определенный интеграл, основные теоремы.

К понятию определенного интеграла можно прийти при решении задачи нахождения площади криволинейной трапеции АВСD

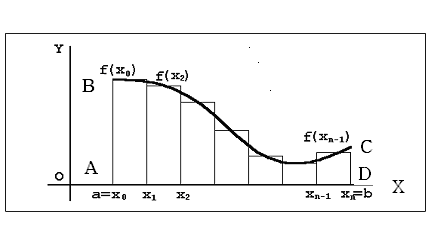
На каждом отрезке [x_i-1,x_i] выберем некоторую точку ξ_i и обозначим ∆x_i=x_i -x_i-1.

Сумму вида будем называть интегральной суммой для функции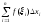

y=f(x) на отрезке [a,b].

Определенным интегралом называется предел n-ой интегральной суммы при

Геометрический смысл определенного интеграла: это площадь криволинейной трапеции, ограниченной слева прямой х=а, справа прямой x=b, сверху кривой y=f(x),снизу осью Ох.

Теорема. Если функция y=f(x) непрерывна на отрезке [a,b], то она интегрируема на этом отрезке.

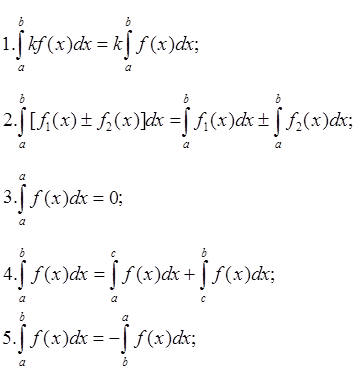
• 6. если 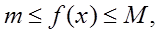то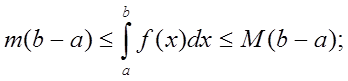

• Теорема о среднем. Пусть функция f(x) непрерывна на [a,b], тогда найдется такая точка 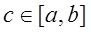, что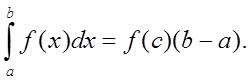

• Если функция y=f(x) интегрируема на отрезке [a,b], то она интегрируема также на произвольном отрезке [a,х], вложенном в [a,b]. Положим

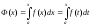
• где х принадлежит отрезку [a,b].

• Функция Ф(х) называется интегралом с переменным верхним пределом.

• Теорема. Пусть функция y=f(x) непрерывна на интервале [a,b] и F(x) –любая первообразная для f(x) на [a,b]. Тогда определенный интеграл от функции f(x) на [a,b] равен приращению первообразной F(x) на этом интервале, т. е.

(1)

• Формула (1) – формула Ньютона-Лейбница. Она утверждает, что определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.

• Для вычисления определенного интеграла нужно найти первообразную подынтегральной функции (неопределенный интеграл) и из значения первообразной при верхнем приделе вычесть значение первообразной при нижнем пределе интегрирования.