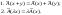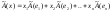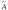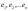математика в виде шпор 25-50

26.N- мерный вектор и векторное пространство

N-мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде Х=(х₁,х₂,…х_n) , где х_i – i-я компонента вектора Х.

Два n-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е. Х=У, если x_i=y_i, i=1…n.

Определение Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие приведённым выше свойствам, называется векторным пространством.

Определение Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее свойствам (1-5) называется Евклидовым пространством.

• Векторное пространство R, называется n-мерным, если в нем существует n линейно независимых векторов, а любые n+1 векторов уже являются зависимыми.

• Число n называется размерностью векторного пространство R и обозначается dim(R).\

27. Системы векторов, операции над ними.

• Суммой двух векторов одинаковой размерности n называется вектор Z=X+Y, компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е. z_i=x_i+y_i , i=1…n.

• Произведением вектора Х на действительное число λ называется вектор V=λX, компоненты которого равны произведению λ на соответствующие компоненты вектора Х, т.е. v_i=λx_i , i=1…n.

Линейные операции над векторами удовлетворяют следующим свойствам:

1. Х + У = У + Х; (коммутативное свойство суммы)

2. (Х + У) + Z = X + (Y + Z); (ассоциативное свойство суммы)

3. a(bX) = (ab)X;

4. a(X + Y) = aX + aY; (дистрибутивное свойство)

5. (a + b)X = aX + bX;

6. Существует нулевой вектор О=(0,0,…0) такой, что Х + О = Х, для любого Х;

7. Для любого вектора Х существует противоположный вектор (-Х) такой, что Х + (-Х) = О;

8. 1∙Х = Х для любого Х.

Скалярным произведением двух векторов и называется число

Свойства скалярного произведения

Угол φ между двумя векторами определяется по формуле:

Два вектора называются ортогональными, если их скалярное произведение равно нулю.

Вектор A_m называется линейной комбинацией векторов A₁,A₂,..,A_m-1 векторного пространства R, если он равен сумме произведений этих векторов на произвольные действительные числа:

A_m = λ₁A₁ + λ₂A₂ + …+ λ_m-1 A_m-1 (1)

Векторы A₁,A₂,..A_m векторного пространства R, называются линейно зависимыми, если существуют такие числа λ₁,λ₂,…λ_m, не равные одновременно нулю, что λ₁A₁ + λ₂A₂ + … + λ_m A_m =0. (2)

В противном случае векторы A₁,A₂,..A_m называются линейно независимыми.

Совокупность n линейно независимых векторов n-мерного пространства R называется базисом.

Теорема. Каждый вектор Х векторного пространства R можно представить, и притом единственным способом, в виде линейной комбинации векторов базиса.

28. Ранг матрицы

В матрице размера m x n вычеркиванием каких-либо строк и столбцов можно выделить квадратные подматрицы k-го порядка, где k≤min(m; n). Определители таких подматриц называются минорами k-го порядка матрицы А.

Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.

Ранг матрицы А обозначается rang A или r(A).

Из определения следует:

1) ранг матрицы размера m x n не превосходит меньшего из её размеров, т.е. r(A) ≤ min (m; n).

2) r(A)=0 тогда и только тогда, когда все элементы матрицы равны нулю, т.е. А=0.

3) Для квадратной матрицы n-го порядка r(A) = n тогда и только тогда, когда матрица А – невырожденная.

В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются элементарные преобразования, сохраняющие ранг матрицы:

1) Отбрасывание нулевой строки (столбца).

2) Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.

3) Изменение порядка строк (столбцов) матрицы.

4) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

5) Транспонирование матрицы.

Теорема. Ранг матрицы не изменится при элементарных преобразованиях матрицы.

С помощью элементарных преобразований можно привести матрицу к ступенчатому виду:

Ранг ступенчатой матрицы равен r ,

так как имеется минор r-го порядка неравный нулю │А│= а₁₁∙а₂₂ ∙…∙а_rr.

29. Линейные операторы и матрицы

Определение. Если задан закон (правило), по которому каждому вектору x пространства ставится в соответствие единственный вектор y пространства то говорят: что задан оператор (преобразование, отображение) A(x), действующий из в и записывают y=A(x).

Оператор называется линейным, если для любого вектора x и y пространства и любого числа λ выполняются следующие соотношения:

Выберем в пространстве базис

и запишем разложение произвольного вектора х по данному базису:

В силу линейности оператора

получим:

т.к так же вектор из ,то его можно разложить по базису.

Матрица называется матрицей оператора в базисе , а ранг r матрицы А - рангом

оператора .

Таким образом, каждому линейному оператору соответствует матрица в данном базисе. Справедливо и обратное: Всякой матрице n-го порядка соответствует оператор n-мерного пространства.

Определим действия над линейными операторами:

1. Суммой двух линейных операторов и называется оператор определяемый

равенством

2. Произведением линейного оператора на число λ называется оператор

определяемый

Произведением линейных операторов и называется оператор

определяемый

Определим нулевой оператор переводящий все векторы пространства в нулевые вектора

и тождественный оператор действующий по правилу

Теорема Матрицы А и А* линейного оператора в базисах е₁,е₂, ..е_n и е₁^*,е₂^*, ..е_n^* связаны соотношением А*=С^-1АС, где С – матрица перехода от старого базиса к новому.

30. Собственные векторы линейных операторов

Вектор Х , не равный нулю, называется собственным вектором матрицы А, если найдется такое число λ, что АХ = λХ.

Число λ называется собственным значением матрицы А, соответствующим вектору Х.

Уравнение

называется характеристическим уравнением матрицы А.

31.Решение системы линейных уравнений с помощью определителей. Формулы Крамера.

Метод Крамера

Теорема Крамера. Пусть Δ – определитель матрицы системы А, а Δ_j – определитель матрицы, полученный из матрицы заменой j-го столбца столбцом свободных членов. Тогда если Δ не равен нулю, то система имеет единственное решение, определённое по формулам Крамера:

где j=1..n.

32. Решиение системы матричной формы

Система m линейных уравнений с n переменными имеет вид:

где a_ij, b_i (i =1..m; j =1..n) – произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений.

Решением системы (1) называется такая совокупность n чисел (x₁=k₁, x₂=k₂, … x_n=k_n), при подстановке которых в (1) каждое уравнение системы обращается в верное равенство.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

Совместная система, называется определенной,

если она имеет единственное решение, и

неопределенной, если она имеет более одного

решения.

Запишем систему (1) в матричной форме. Обозначим: где А – матрица коэффициентов при переменных, или матрица системы, Х – матрица-столбец переменных; В – матрица-столбец свободных членов.Систему (1) можно записать в виде: АХ=В.

33. Метод Гаусса.

Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого или треугольного вида.

Рассмотрим матрицу:

эта матрица называется расширенной матрицей системы (1), так как в нее кроме матрицы системы А, дополнительно включен столбец свободных членов

34. Сущность и условия применения теории вероятностей.Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях. Случайное явление – это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному. Методы теории вероятности по природе приспособлены только для исследования массовых случайных явлений; они не дают возможность предсказать исход отдельного случайного явления, но дают возможность предсказать средний суммарный результат массы однородных случайных явлений. Т.в. служит для обоснования матем и прикладной стат-ки.к-я исп-ся при планир-иии орган-ции произ-ва и др.

35. Основные понятия ТВ.

В теории вероятностей испытанием принято называть эксперимент, который (хотя бы теоретически) может быть произведён в одних и тех же условиях неограниченное число раз.

Результат или исход каждого испытания назовём событием. Событие является основным понятием теории вероятностей. Будем обозначать события буквами А, В, С.

Виды событий:

• достоверное событие - событие, которое в результате опыта обязательно произойдет.

• невозможное событие - событие, которое в результате опыта не может произойти.

• случайное событие - событие, которое может произойти в данном опыте, а может и не произойти.

Виды событий

• Случайные события A₁,A₂,…,A_n образуют полную группу событий, если в результате испытания непременно должно появиться хотя бы одно из них .

• Случайные события A₁,A₂,…,A_n называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

• Случайные события A₁,A₂,…,A_n называются единственно возможными, если в результате испытаний происходит какое-либо одно и только одно из этих событий.

• Равновозможные события - несколько событий в данном опыте, ни одно из которых не является объективно более возможным, чем другое.

Классическое определение вероятности основано на понятии равновозможности событий.

Равновозможность событий означает, что нет оснований предпочесть какое-либо одно из них другим.

Рассмотрим испытание, в результате которого может произойти событие A. Каждый исход, при котором осуществляется событие A, называется благоприятным событию A.

Вероятностью события A (обозначают P(A)) называется отношение числа исходов, благоприятных событию A (обозначают k), к числу всех исходов испытания – N т.е. P(A)= k/ N.

Из классического определения вероятности вытекают следующие ее свойства:

• Вероятность любого события заключена между нулем и единицей.

• Вероятность достоверного события равна единице.

• Вероятность невозможного события равна нулю

Статистическое определения вероятности

• Пусть произведена серия из N испытаний, в каждом из которых могло появиться или не появиться событие А. Тогда абсолютной частотой (или частотой) F называется число появлений события А, а относительной частотой (или частостью) f(A)—отношение абсолютной частоты к общему числу испытаний: f(A)= F/N.

• f(А)P(A) при N  

36. Вероятностное пространство 

Вероятностное пространство — это математическая модель случайного эксперимента (опыта) в аксиоматике А. Н. Колмогорова. Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, необходимую для его математического анализа средствами теории вероятностей. Любая задача теории вероятностей решается в рамках некоторого вероятностного пространства, полностью заданного изначально. Задачи, в которых вероятностное пространство задано не полностью, а недостающую информацию следует получить по результатам наблюдений, относятся к области математической статистики.

37. Элементы комбинаторного анализа

Основные задачи комбинаторного анализа – размещение объектов в соответствии со специальными правилами и нахождение числа способов, которыми это можно сделать.

Если правила просты, то основным является подсчет числа возможностей для осуществления искомого размещения. Если правила тонкие или запутанные, то главной проблемой становится вопрос существования таких размещений и нахождения методов их построения.

Пусть дано множество S произвольной природы.

Определение 1. Размещением объема k элементов множества S называется упорядоченная выборка k элементов из множества S.

Определение 2. Сочетанием объема k называется неупорядоченная выборка k элементов множества S.

Определение 3. Размещение (сочетание) называется размещением (сочетанием) с повторением или с возвращением,  если элементы в нем могут повторяться.

38.  События А и В называются равными, если осуществление события А влечет за собой осуществление события В и наоборот.  Объединением или суммой событий А_k называется событие A, которое означает появление хотя бы одного из событий А_k..Пересечением или произведением событий A_k  называется событие А, которое заключается в осуществлении всех событий A_k.   Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В..Дополнительным к событию А называется событие , означающее, что событие А не происходит.Элементарными исходами опыта называются такие результаты опыта, которые взаимно исключают друг друга и в результате опыта происходит одно из этих событий, также каково бы ни было событие А, по наступившему элементарному исходу можно судить о том, происходит или не происходит это событие.Совокупность всех элементарных исходов опыта называется пространством элементарных событий.

39. Теоремы сложения вероятностей.

• Теорема сложения. Если А и В несовместны, то Р(А + В) = Р(А) +Р(В)

Есл и противоположные события, то

Теорема сложения вероятностей

Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Следствие 1: Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.

Определение. Противоположными называются два несовместных события, образующие полную группу.

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

Следствие 2: Сумма вероятностей противоположных событий равна единице.

Определение. Событие А называется независимым от события В, вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

40.Теоремы умножения вероятностей.

• Теорема умножения. Если А и В независимые события, то

• Р(АВ) = Р(А)Р(В).

• Если А и В совместны, то теорема сложения принимает вид:

• Р(А+В)=Р(А)+Р(В)  Р(АВ) .

Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.

41.Формула полной вероятности.

Пусть событие А может наступить при условии реализации одной из гипотез Н₁, Н₂, ..., Н_n, образующих полную группу событий.

Тогда

. (1)

Формула (1) называется формулой полной вероятности.

42. Теорема Байеса 

Теорема Байеса — одна из основных теорем элементарной теории вероятностей, которая определяет вероятность наступления события в условиях, когда на основе наблюдений известна лишь некоторая частичная информация о событиях. Иначе, по формуле Байеса можно более точно пересчитывать вероятность, беря в учет как ранее известную информацию, так и данные новых наблюдений.

• Предположим, что в результате испытания событие А произошло. Какова вероятность, что событие А произошло в результате реализации гипотезы Н_k , т.е. P(H_k/A) = ? (происходит переоценка вероятностей гипотез). Ответ дает формула Байеса:

или

 — априорная вероятность гипотезы A;

 — вероятность гипотезы A при наступлении события B (апостериорная вероятность);

 — вероятность наступления события B при истинности гипотезы A;

 — вероятность наступления события B.

 — математическая формула априорной вероятности наступления события B , где суммирование идет по всем гипотезам Ai;

43. Формула Бернулли

Формула Бернулли — формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний.

Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность P_k,n того, что событие A наступит k раз в n независимых испытаниях, равна:  где q = 1-p.

44.Случайные величины. Способы их описания.

Дисперсией D(X) случайной величины называется математическое ожидание квадрата ее отклонения от математического ожидания:

D(X) = M[Х-M(X)]² или D(X) = M[X-a]² , где а = М(Х). Часто вместо дисперсии используют среднее квадратическое отклонение:

Свойства дисперсии случайной величины.

1. Дисперсия постоянной величины равна нулю: D(С) = 0.

2. Постоянный множитель можно выносить за знак дисперсии, возводя его и квадрат : D(кХ) = к²D(X)

3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом математического ожидания D(X) = М(Х²)-[М(Х)]².

Функция распределения случайной величины

Пусть дана функция F(x) определённая следующим образом: для каждого х значение F(x) равно вероятности того, что дискретная величина X примет значение, меньшее х, F(x) = Р(Х<х). Эта функция называется интегральной функцией распределения.

Функция распределения  самая универсальная характеристика случайной величины.

Ее свойства:

1. Функция распределения  неубывающая функция. F(x₂) ≥F(x₁), если х₂>x₁.

2. 0 ≤ F(x) ≤ 1.

3. Вероятность того, что случайная величина X лежит в пределах

х₁ < X < х₂ , т.е. P(х₁ < X < х₂) вычисляется как Р(х₁ < Х < х₂) = F(x₂) ─ F(x₁).

График функции распределения представляет собой график возрастающей функции, значения которой начинаются с 0 и кончаются 1.

45.Основные числовые характеристики дискрет. случ. величин.

Законы распределения дискретных случайных величин.

Дискретная случайная величина X имеет биномиальный закон распределения, если она принимает значения 0,1, 2,…,m,….,n с вероятностями р(m) = Р(Х = m) = C_n^m р^m q^n-m, где 0 < p <1, q = 1─ р.

Биномиальный закон распределения представляет собой закон распределения числа Х = m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.

Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по биномиальному закону, даются формулами

M(X) = np, D(X) = npq.

Следствие. Математическое ожидание величины (m/n) в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью р, равно р, т.е. M(m/n) = р, D(m /n)=pq/n.

Законы распределения дискретных случайных величин. Paспределение Пуассона.

Дискретная случайная величина X имеет закон распределения Пуассона, если она принимает значения 0,1 2,…,m,…,n с вероятностями р(m) = Р(Х=m) =е^─λ λ^m/m! , где λ = np.

Tеорема. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона. т.е. М(Х) = λ, D(X)= λ.

Распределение Пуассона ─ частный случай биномиального закона распределения для относительно больших n и относительно малых р.