
Эконометрика. Учебное пособие
.pdf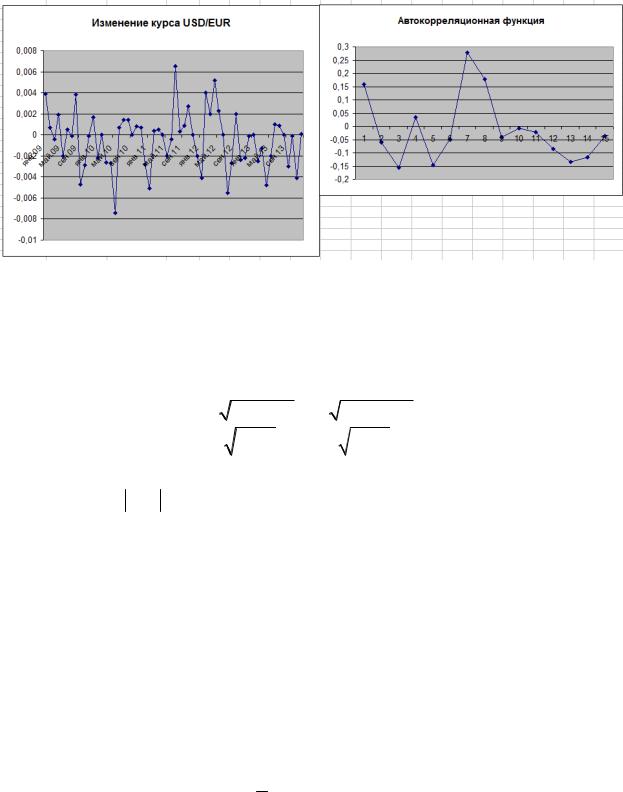
Рис. 5.6. Изменение курса USD/EUR
Отметим, что для данного ряда все r не значимы, т.е. ряд можно считать чисто случайным. Это можно установить с помощью критерия Стьюдента (см. раздел 1.4). Например, проверим гипотезу H0 :r7 0 (из рисунка видно, что r7 0,28 является максимальным значением). Получаем
T |
r |
n 2 |
|
r7 |
50 7 2 |
1,86, |
||||
|
|
|
|
|
|
|
|
|||
набл |
1 r2 |
|
|
1 r2 |
|
|||||
|
|
|
|
|
||||||
|
|
|
|
|
|
7 |
|
|
||
tкр СТЬЮДРАСПОБР(0,05;50 7 2) 2,09.
Поскольку Tнабл tкр , то оснований для отвержения гипотезы H0 нет.
5.3. Выделение тенденции при помощи скользящего среднего
Одна из основных целей анализа временного ряда заключается в выделении тренда и сезонной составляющей. Для этого часто используется такой инструмент, как скользящее среднее.
Скользящее среднее – это среднее арифметическое значений исходного ряда за установленный период. Этот период называется порядком (длинной или временным окном) скользящего среднего.
Если порядок k скользящего среднего является нечетным числом, т.е. k 2s 1, то вычисленное значение скользящей средней ставят в соответствие моменту времени, который является серединой периода. Т.е. в этом случае значения скользящих средних вычисляют по формуле
|
1 |
t s |
|
ytc |
yj |
||
k |
|||
|
j t s |
для t принимающего значения от s 1 до n s 1 .
Если порядок k скользящего среднего является четным числом, т.е. k 2s, то скользящее среднее рассчитывают по этой же формуле, однако вы-
81
численное значение ставят в соответствие середине между моментами времени t и t 1 , т.е. можно написать
1 t s 1 ytc 0,5 k j t s yj
для t принимающего значения от s до n s 1 , т.е. для первых s и для по-
следних s значений скользящее среднее не рассчитывается.
Для того чтобы избавиться от дробных индексов, переходят к, так назы-
ваемой, центрированной скользящей средней – для полученного ряда сколь-
зящих средних вычисляют скользящие средние порядка 2.
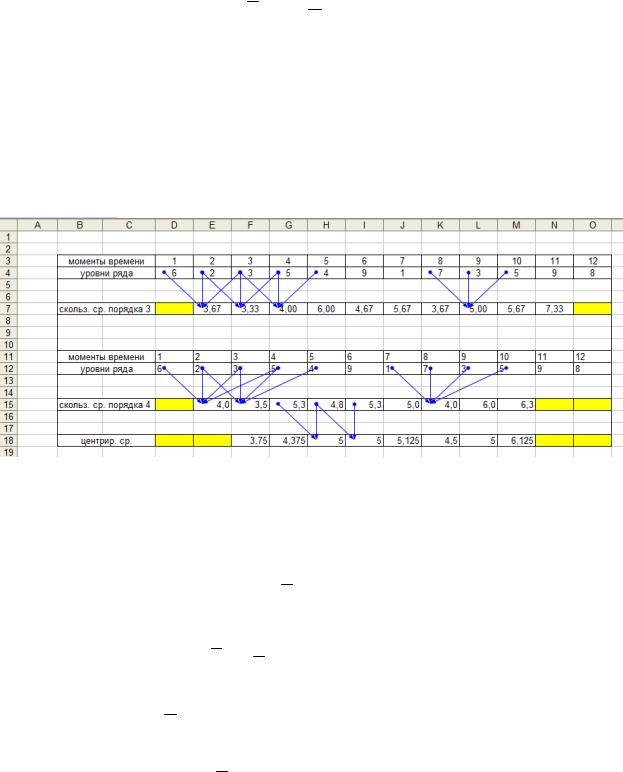
Процесс вычисления скользящего среднего наглядно представлен на рисунке 5.7.
Рис. 5.7. Вычисление скользящей средней
Отметим важное свойство скользящего среднего: если уровни ряда зави-
сят от времени линейно, т.е. yt a bt, то значения скользящего среднего лю-
бого порядка будут совпадать с уровнями исходного ряда, т.е.
ytc yt .
Проверим это свойство для скользящего среднего порядка 3:
ytc 1(yt 1 yt yt 1)
3
1(a b(t 1) a bt a b(t 1)) 3
1(3a 3bt) a bt yt. 3
Скользящее среднее убирает высокочастотные колебания уровней ряда. Это означает, что удаляются случайная составляющая и циклическая компо-
82
нента с периодом меньшим, чем порядок скользящего среднего. С помощью скользящего среднего можно выявить тенденцию ряда. Собственно говоря, ряд из скользящих средних подходящего порядка и является тенденцией исходного временного ряда.
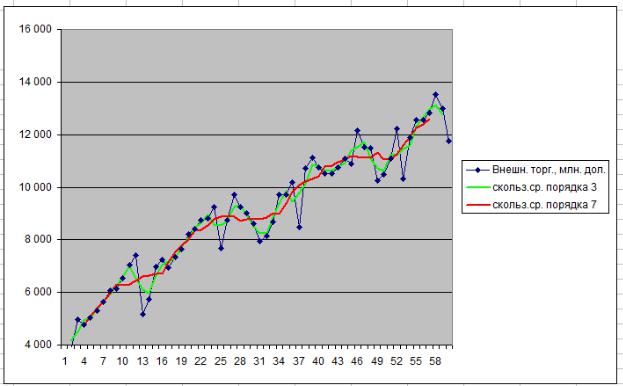
Пример 19. На рис. 5.8 изображены скользящие средние для временного ряда из примера 15. Видно, что скользящее среднее порядка 7 является более гладким, чем скользящее среднее порядка 3.
Рис. 5.8. Скользящее среднее временного ряда
Какой порядок скользящего среднего является наиболее подходящим? Для того чтобы ответить на этот вопрос, необходимо рассмотреть аддитивную модель ряда
Yt Tt St Et ,
где t – моменты времени, Tt – уровни тренда, St – уровни сезонной компонен-
ты, Et – уровни случайной компоненты. Относительно случайной компоненты
будем считать выполненными все предпосылки МНК, в частности, будем предполагать, что
n
Et 0.
t 1
Пусть коррелограмма выявила наличие сезонных колебаний с периодом. Будет естественно и разумно предположить, что за период сезонные колебания взаимопогашаются, т.е.
83

k
Sj 0.
j k
Как правило, для рядов экономических данных 12 (для помесячных данных) или 4 (для поквартальных данных).
Вычисление скользящего среднего порядка дает
Yt c Ttc Stc Etc Ttc Etc ,
поскольку Stc 0.
Если ряд имеет линейную тенденцию, то выше было показано, что Tt c Tt , следовательно,
|
|
c T |
|
|
|
Y |
Ec . |
||||
|
t |
t |
|
t |
|
Если тенденция ряда является нелинейной, то Tt c Tt , однако, для мно-
гих нелинейных зависимостей при не очень больших значениях будет выпол-
няться приближенное равенство Tt c Tt , значит,
|
|
c T |
|
|
|
Y |
Ec . |
||||
|
t |
t |
|
t |
|
Величина Etc будет близка к нулю, следовательно,
Yt c Tt .
Вывод: скользящее среднее, порядок которого равен периоду сезонной составляющей, будет совпадать (приближенно) с тенденцией временного ряда. Разность между уровнями временного ряда и соответствующими значениями этого скользящего среднего является оценкой сезонной компоненты.
Пример 20. Для ряда из примера 15 «наилучшее» скользящее среднее имеет порядок 12 (это следует из вида коррелограммы). На рис. 5.9 изображены «наилучшее» скользящее среднее, а также оценка сезонной компоненты. Расчеты, необходимые для построения диаграммы, представлены на рис. 5.10 и рис. 5.11.
84
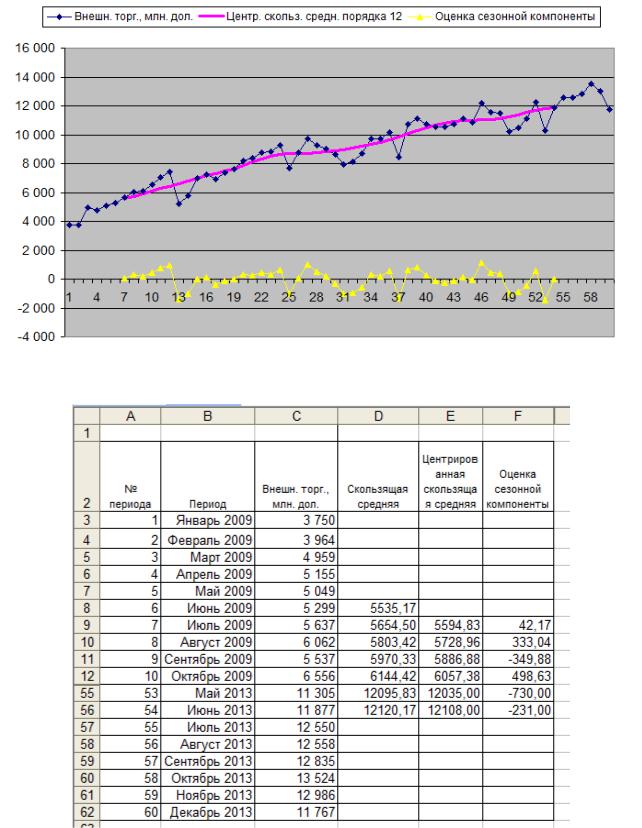
Рис. 5.9. Скользящее среднее «наилучшего» порядка и оценка сезонной компоненты
Рис. 5.10. Расчет скользящей средней и оценки сезонной компоненты (строки 13-52 скрыты)
85
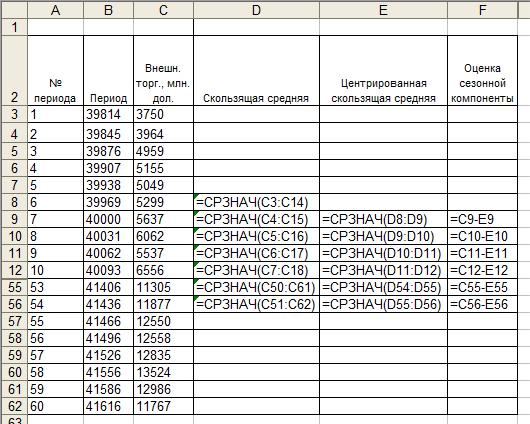
Рис. 5.11. Формулы для расчета скользящей средней и оценки сезонной компоненты (строки 13-52 скрыты)
После того как получена оценка сезонной компоненты, необходимо ее очистить от влияния случайной составляющей. Это можно осуществить следующим образом:
Находим средние оценки сезонной компоненты по каждому моменту времени. Для этого необходимо просуммировать оценки сезонных компонент для моментов времени отстоящих друг от друга на расстоянии равном периоду сезонной компоненты и полученную сумму разделить на их количество.
Исходя из условия взаимопогашения сезонных воздействий, определяем корректирующий коэффициент, который равен среднему значению всех средних оценок сезонной компоненты, полученных в предыдущем пункте.
Рассчитываем скорректированные значения сезонных компонент как разность между средними оценками сезонной компоненты и корректирующим коэффициентом.
Пример 21. Результаты применение данной схемы для временного ряда из примера 15 представлены на рис. 5.12 – 5.14.
86
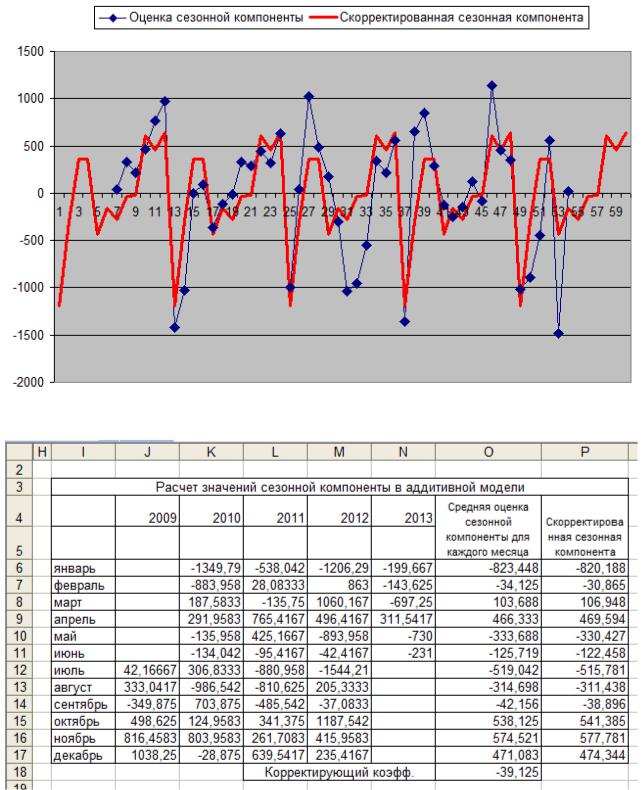
Рис. 5.12. Скорректированная сезонная компонента
Рис. 5.13. Расчет скорректированной сезонной компоненты
87
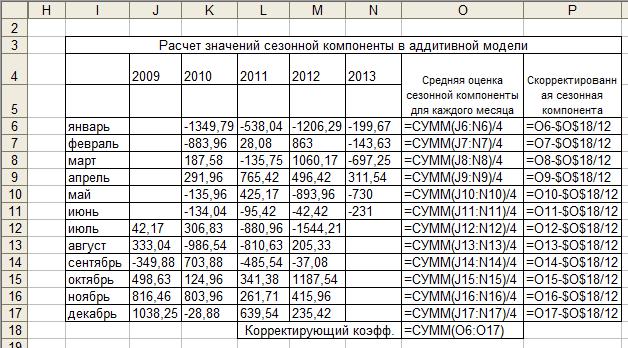
Рис. 5.14. Формулы для расчета скорректированной сезонной компоненты
Разность уровней исходного ряда и скорректированной сезонной компоненты – это ряд, который содержит только тенденцию и случайную составляющую. Для такого ряда можно получить тенденцию используя стандартные методы построения уравнения линейной регрессии (см. пример 4), например,
инструмент Линия тренда.
Пример 22. Соответствующие результаты для ряда из примера 15 представлены на рисунке 5.15.
88
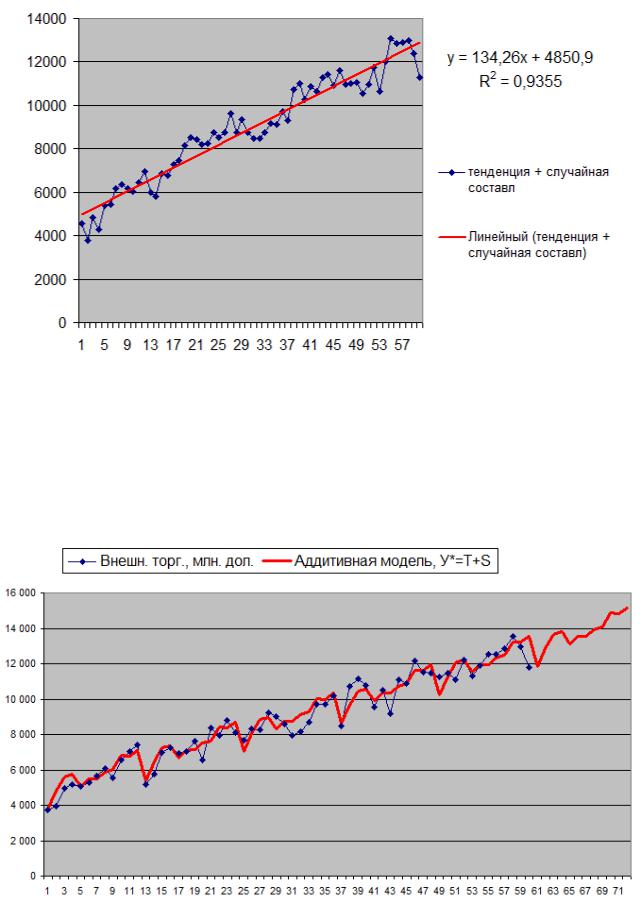
Рис. 5.15. Линейный тренд
Суммируя соответствующие уровни линейного тренда и скорректированной сезонной компоненты, получаем аддитивную модель ряда, очищенную от случайной компоненты. Такая модель может быть использована для прогнозирования.
Пример 23. Аддитивная модель и прогноз на один год для ряда из примера 15 представлены на рис. 5.16.
Рис. 5.16. Аддитивная модель
89
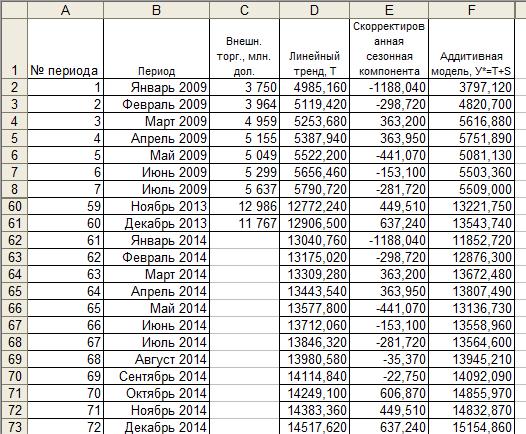
Рис. 5.17. Расчет аддитивной модели (строки 9-59 скрыты)
90
