
Эконометрика. Учебное пособие
.pdf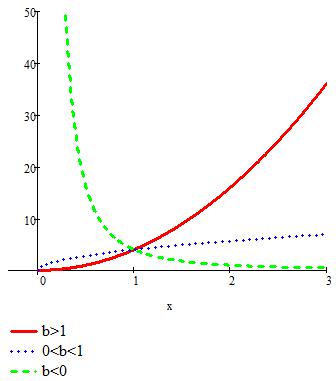
Степенная зависимость.
Рис. 3.7. График степенной зависимости y a xb
Свойства степенной зависимости существенно зависят от значения коэффициента b. Если b 1, то степенная функция возрастает и выпукла вниз, если 0 b 1, то она возрастает и выпукла вверх, а если b 0, то она убывает и выпукла вниз.
41
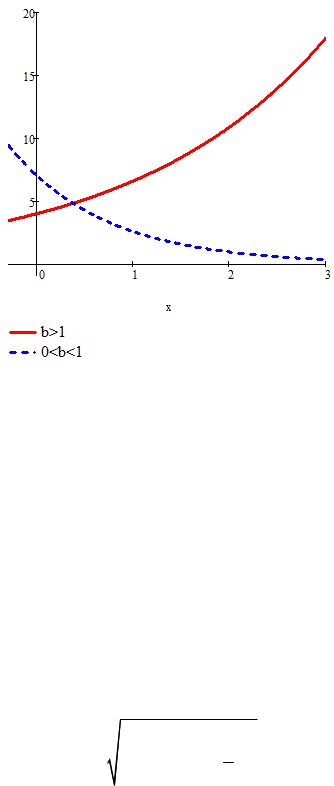
Показательная зависимость.
Рис. 3.8. График показательной зависимости y a bx
Свойства показательной зависимости существенно зависят от значения коэффициента b. Если b 1, то функция возрастает и выпукла вниз, если 0 b 1, то она убывает и выпукла вниз.
При выборе вида зависимости также необходимо иметь ввиду, что обычно степенная функция моделирует зависимости с постоянной эластичностью; показательная функция моделирует зависимости с постоянным темпом роста; логарифмическая функция моделирует зависимости с постоянным уменьшением прироста; гиперболическая функция моделирует зависимости с нижним или верхним пределом.
3.4. Индексы корреляции и детерминации
Уравнение нелинейной регрессии, так же как и в случае линейной зависимости, дополняется показателем корреляции, а именно индексом корреля-
ции R
R |
1 |
(yi |
yi*)2 |
. |
|||
(yi |
y |
)2 |
|||||
|
|
|
|||||
Величина индекса корреляции не превосходит единицу; чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии. Индекс корреляции, в отличии от коэффициента корреляции, может быть не определен. Возможна такая выборка, что подкоренное выражение будет отрицательным!
42
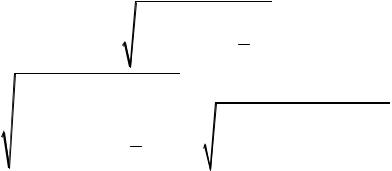
Следует различать понятия индекс корреляции и коэффициент корреля-
ции, последнее применяется только для линейной зависимости. Для линейной зависимости индекс корреляции R совпадает с коэффициентом корреляции r. Как было показано в пункте 3.2, нелинейные модели сводятся к линейным. Поэтому возникает естественный вопрос: как связаны между собой индекс корреляции R нелинейной модели и коэффициент корреляции r соответствующей линейной модели?
Для гиперболической и логарифмической зависимостей R r, так как значения показателей R и r зависят только от значений зависимой переменной, а эти значения не меняются при линеаризации. При этом очевидно, что равенство R r справедливо для любой модели нелинейной по независимой переменной.
В случае модели, которая нелинейна по параметрам ситуация несколько иная. Рассмотрим, например, степенную зависимость. В этом случае нелинейная регрессия и соответствующая линейная модель будут иметь вид
|
|
|
|
|
|
|
|
|
|
|
|
|
y* axb , |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(y |
) lna bx |
|
|
|
|
|
|
|||||||||||
* |
|
ln y |
* |
, x |
|
lnx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где (y |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
R |
1 |
(yi |
|
yi*)2 |
, |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
(yi |
y |
)2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
* |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
yi yi |
|
|
|
|
|
|
|
|
(ln yi |
* |
2 |
|
||||||
|
|
r |
1 |
|
|
|
|
|
|
|
|
1 |
ln yi ) |
. |
|||||||||||||
|
|
(yi |
y |
)2 |
|
|
(ln yi |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln yi )2 |
||||||||||||
Таким образом, для степенной зависимости R r. Аналогичный результат справедлив и для показательной зависимости.
Величину R2 для нелинейных связей называют индексом детерминации (напомним, что для линейной связи аналогичная величина называется – коэффициент детерминации). Индекс детерминации показывает долю вариации результативной переменной Y, обусловленную вариацией факторного признака Х. Он не может превосходить единицу.
3.5. Средняя ошибка аппроксимации
Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии. Чем меньше эти отличия, тем ближе теоретические значения к эмпирическим данным, тем лучше качество модели. Величина отклонений фактических и расчетных значений результатив-
ного признака y y* по каждому наблюдению представляет собой ошибку
43
аппроксимации. Поскольку y y* может быть величиной как положитель-
ной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
Отклонения y y* можно рассматривать как абсолютную ошибку ап-
проксимации, а
y* y 100% y
как относительную ошибку аппроксимации. Для того чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, находят среднюю ошибку аппроксимации как среднюю арифметическую простую
A 1 (yi yi*) 100%. n yi
Модель считается точной, если A 10%.
3.6. Коэффициент эластичности
Коэффициент эластичности данной функции y f (x) – это функция,
заданная следующим образом
E(x) |
dy x |
|
|
|
|
|
x |
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
dx y |
|
f (x) |
|
|
|
||||||||||||||
|
|
|
|
|
|
f (x) |
|
|
|
|
|||||||||
Раскроем смысл этого определения. Пусть x и y – приращения аргу- |
|||||||||||||||||||
мента и функции в точке (x,y). Тогда величины |
x |
y |
|||||||||||||||||
|
|
|
и |
|
показывают отно- |
||||||||||||||
|
x |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|||
сительную величину приращений. Рассмотрим отношение |
|||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
y x |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
E y x |
|
|
|
|
|||||||||||||||
|
|
|
. |
|
|
|
|
||||||||||||
x |
y |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
Это отношение похоже на отношение y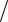 x, которое используется в определении производной. Однако, отношение y
x, которое используется в определении производной. Однако, отношение y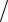 x характеризует абсолют-
x характеризует абсолют-
ные изменения аргумента и функции, а E - относительные. Перейдем к пределу:
lim E |
lim |
y |
|
x |
|
x |
lim |
y |
|
x |
|
dy |
E(x). |
|
|
|
|
|
|
||||||||
x 0 |
x 0 x y |
|
y x 0 x y dx |
||||||||||
|
|
|
|
|
44 |
|
|
|
|
|
|
||

|
Таким образом, E(x) |
– предел отношения относительных изменений. |
|||
Если |
x увеличился на 1%, |
то это означает, что x 0,01x, следовательно, |
|||
|
y |
|
|
|
|
E |
|
100. Т.е. при x 0,01x величина E показывает на сколько процен- |
|||
|
y |
y, если x изменится на 1%. |
Если величина 0,01x мала, то |
||
тов изменится |
|||||
можно считать, что предельное значение E(x) |
показывает на сколько процен- |
||||
тов изменится |
y если x изменится на 1%. |
Хотя это утверждение является |
|||
лишь приближенным, его часто приводят в качестве определения коэффициента эластичности.
Приведем выражения коэффициентов эластичности для наиболее распространенных типов функций.
|
|
|
|
|
|
|
|
|
Таблица 3.1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
Вид зависимости |
Производная |
Коэффициент эла- |
|||||||||
dy/dx |
стичности |
||||||||||
|
|
|
|||||||||
линейная |
b |
|
bx |
||||||||
y a bx |
|
|
|
|
|||||||
|
a bx |
||||||||||
|
|
|
|
|
|
|
|
||||
логарифмическая |
|
b |
|
b |
|||||||
y a bln x |
|
|
|
|
|
|
|
|
|||
|
x |
|
a blnx |
||||||||
|
|
|
|
|
|||||||
гиперболическая |
|
|
b |
|
|
b |
|
||||
y a |
b |
|
|
|
|
||||||
|
2 |
|
|
ax b |
|||||||
|
|
||||||||||
|
x |
|
|
x |
|
||||||
|
|
|
|
|
|
|
|
|
|||
степенная y axb |
abxb 1 |
b |
|||||||||
показательная y abx |
a lnb bx |
|
xlnb |
||||||||
Как видно из таблицы, степенная функция (и только она) имеет постоянный коэффициент эластичности, поэтому экономические зависимости с постоянной эластичностью обычно моделируются степенными функциями. Также отметим, что показатель b имеет простой экономический смысл: b показывает на сколько процентов изменяется y, когда x увеличивается на 1%.
В экономических расчетах также часто используется обобщенный коэф-
фициент эластичности
|
|
|
|
|
|
x |
|
|
|
E(x) f |
|
||||||||
|
|
, |
|||||||
(x) |
|||||||||
|
|
|
|
|
|
f ( |
x |
) |
|
1
где x n xi .
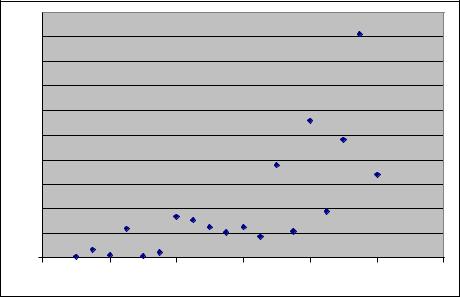
Пример 10. Пусть дана выборка
45
X |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
4,5 |
5,0 |
5,5 |
Y |
0,5 |
6,3 |
2,3 |
23,5 |
1,6 |
4,2 |
33,7 |
30,4 |
24,8 |
21,0 |
|
|
|
|
|
|
|
|
|
|
|
X |
6,0 |
6,5 |
7,0 |
7,5 |
8,0 |
8,5 |
9,0 |
9,5 |
10,0 |
10,5 |
Y |
25,0 |
16,8 |
75,2 |
21,7 |
111,9 |
37,9 |
96,1 |
182,2 |
67,7 |
232,4 |
По этим данным необходимо подобрать наилучшую модель парной регрессии. |
||||||
Построим поле корреляции (рис. 3.9). |
|
|
|
|
||
200 |
|
|
|
|
|
|
180 |
|
|
|
|
|
|
160 |
|
|
|
|
|
|
140 |
|
|
|
|
|
|
120 |
|
|
|
|
|
|
100 |
|
|
|
|
|
|
80 |
|
|
|
|
|
|
60 |
|
|
|
|
|
|
40 |
|
|
|
|
|
|
20 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
12 |
|
|
Рис. 3.9. Поле корреляции |
|
|
||
Визуальный анализ поля корреляции показывает, что между данными есть зависимость, которая задается возрастающей и выпуклой вниз функцией, например, такой, как показано на рисунке 3.10.
46
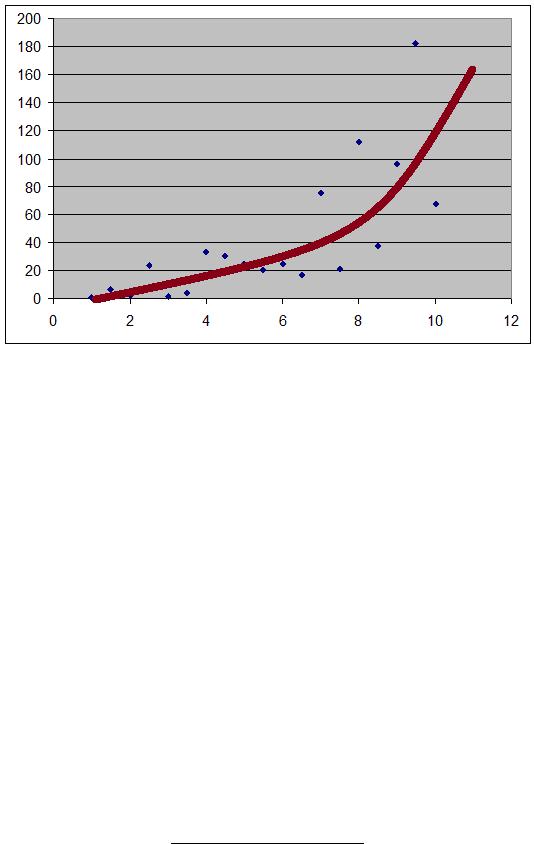
Рис. 3.10. Возможная зависимость
Безусловно, визуальный анализ не может служить надежной основой для каких бы то ни было выводов. Поэтому необходимо построить линейную и нелинейные модели и найти их коэффициенты детерминации. В данном примере воспользуемся инструментом Линия тренда (правый щелчок мыши на любой точке корреляционного поля, затем выбираем вид зависимости и устанавливаем флажки Показывать урав-
нение на диаграмме и Поместить на диаграмму величину достоверности аппрок-
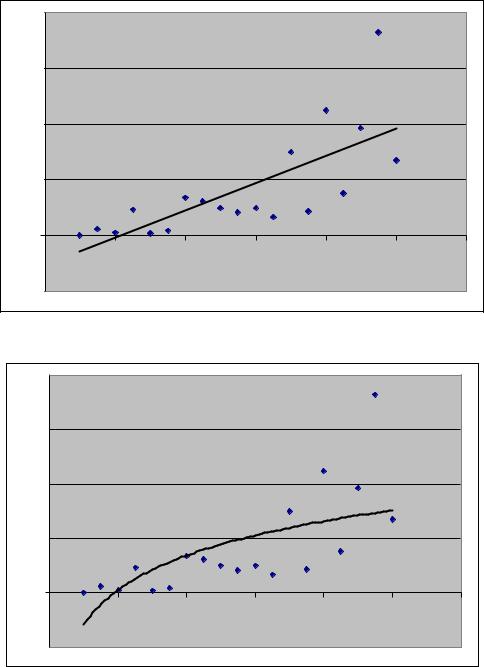
симации R^21). Результаты представлены на рисунках 3.11 – 3.14.
1 В терминологии Microsoft Excel, достоверность аппроксимации – это коэффициент детерминации линеаризованного уравнения. То есть эта величина совпадает с индексом детерминации нелинейной зависимости только для логарифмической зависимости, а для степенной и экспоненциальной это не так (см. раздел 3.4). Однако этот показатель также можно использовать для оценки качества уравнения.
47
200 |
|
|
|
|
|
|
|
|
y = 12,187x - 25,832 |
|
|
|
|
150 |
|
R2 = 0,5361 |
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
50 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
12 |
-50 |
|
|
|
|
|
|
|
|
Рис. 3.11. Линейная регрессия |
|
|
||
200 |
|
|
|
|
|
|
|
y = 45,505Ln(x) - 28,655 |
|
|
|
|
|
150 |
|
R2 = 0,4108 |
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
50 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
12 |
-50 |
|
|
|
|
|
|
|
Рис. 3.12. Логарифмическая зависимость |
|
||||
48
200 |
|
|
|
|
|
|
180 |
y = 0,9196x1,9774 |
|
|
|
|
|
160 |
|
|
|
|
||
R2 = 0,7228 |
|
|
|
|
||
140 |
|
|
|
|
||
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
100 |
|
|
|
|
|
|
80 |
|
|
|
|
|
|
60 |
|
|
|
|
|
|
40 |
|
|
|
|
|
|
20 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
12 |
|
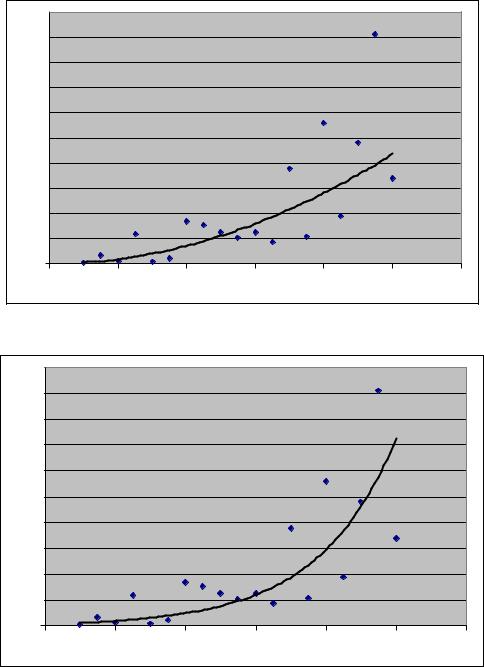
Рис. 3.13. Степенная зависимость |
|
|
|||
200 |
y = 1,608e0,4503x |
|
|
|
|
|
180 |
|
|
|
|
||
R2 = 0,6819 |
|
|
|
|
||
160 |
|
|
|
|
|
|
140 |
|
|
|
|
|
|
120 |
|
|
|
|
|
|
100 |
|
|
|
|
|
|
80 |
|
|
|
|
|
|
60 |
|
|
|
|
|
|
40 |
|
|
|
|
|
|
20 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
12 |
Рис. 3.14. Экспоненциальная зависимость
Выводы: коэффициент детерминации линейной регрессии не очень высок, да и визуальный анализ свидетельствует о том, что в данном случае зависимость носит нелинейный характер. Среди нелинейных моделей зависимость y=0,9196x1,9774 имеет самый высокий показатель качества (достоверность аппроксимации), поэтому мы приходим к выводу, что в данном случае имеет место степенная зависимость.
49
4. Множественная линейная регрессия
Множественный регрессионный анализ является развитием парного регрессионного анализа применительно к случаям, когда зависимая переменная связана более чем с одной независимой переменной. Рассмотрим, например, следующую модель спроса на продукты питания
y 0 1x 2 p ,
где y – общая величина расходов на питание, x – располагаемый личный до-
ход (первый регрессор), p – цена продуктов питания (второй регрессор).
Очевидно, что такая модель будет более точной, чем парная регрессия, связывающая y только с x или только с p.
Для геометрической иллюстрации этой зависимости необходима трехмерная диаграмма с осями y, x и p. Основание диаграммы содержит оси x и p, и если пренебречь текущим влиянием случайного члена, то координата показывает величину y, соответствующую произвольному сочетанию x и p. Учет случайного члена приводит к тому, что фактическое значение y не будет
лежать на |
данной плоскости. Точки, построенные по данной выборке |
(xi, pi,yi) |
представляют собой трехмерный аналог поля корреляции, которое |
мы ранее использовали при рассмотрении парной регрессии. При этом вместо линии регрессии имеем плоскость регрессии. Уравнение для данной плоскости имеет вид
y b0 b1x b2 p,
где b0 , b1, b2 являются оценками неизвестных параметров 0 , 1, 2 .
Соответствующая трехмерная диаграмма может выглядеть, например, так, как показано на рисунке 4.1.
50
