Эконометрика. Учебное пособие

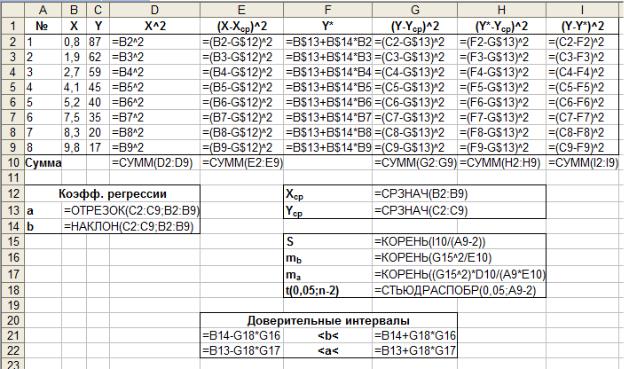
Рис. 2.10. Формулы для расчета доверительных интервалов

Подчеркнем, что доверительные интервалы найдены для уровня значимости

=0,05. То есть это такие интервалы, что коэффициенты теоретического уравнения регрессии принадлежат им с вероятностью 95%.

Пример 7. Результаты примеров 4 – 7 могут быть получены автоматически при помощи встроенного инструмента Microsoft Excel. Для этого необходимо в разделе Анализ данных выбрать инструмент Регрессия. В результате появляется диалоговое окно, которое нужно заполнить так, как показано на рисунке 2.11.

31

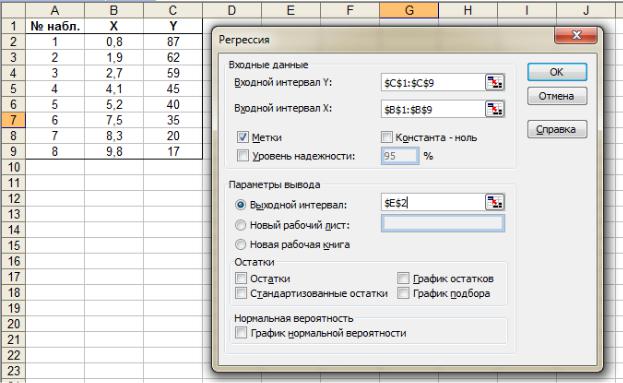
Рис. 2.11. Заполнение диалогового окна Регрессия

Замечание. Обратите внимание, что интервалы $C$1:$C$9 и $B$1:$B$9 содержат заголовки столбцов, а не только числовые данные (для этого ставим флажок Метки). Это удобно при отображении результатов проводимого анализа.

После нажатия на Ок на экран будут выведены результаты регрессионного анализа, которые содержат практически все, что было нами получено в предыдущих примерах (рис. 2.12).

32

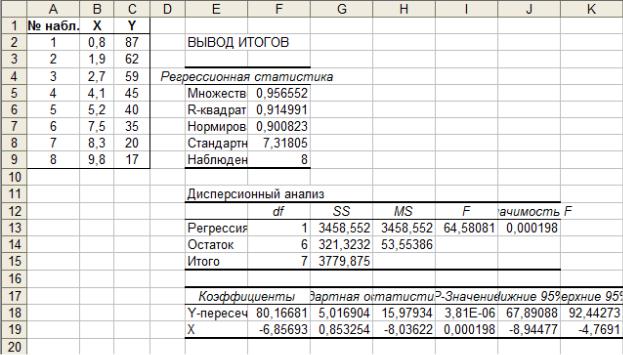
Рис. 2.12. Результаты регрессионного анализа

Поскольку терминология, используемая в Microsoft Excel, несколько отличается от той, которая принята в российской научной литературе (и которая используется в данном пособии), то укажем соответствие между введенными ранее величинами и значениями на рисунке 2.12.

33

3.Парная нелинейная регрессия

3.1.Виды нелинейных регрессий

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью нелинейных функций. Различают два класса нелинейных регрессий:

Регрессии, нелинейные относительно объясняющих переменных, но линейные по оцениваемым параметрам (нелинейные по переменным);

Регрессии, нелинейные по оцениваемым параметрам (нелинейные по параметрам).

Также рассматривают внутренне нелинейные регрессии, однако мы ограничимся двумя вышеуказанными типами.

Примером нелинейной регрессии по включенным в нее объясняющим переменным могут служить следующие функции:

Логарифмическая y ln x ;

К нелинейным регрессиям по оцениваемым параметрам относятся функ-

ции:

Степенная y x ;

Экспоненциальная y x .

Для оценки параметров перечисленных выше регрессий можно воспользоваться методом наименьших квадратов для парной линейной регрессии, который был подробно рассмотрен в предыдущей главе. Однако для этого необ-

ходимо выполнить линеаризацию нелинейного уравнения, т.е. привести его к линейному виду.

3.2. Линеаризация нелинейных регрессий

Рассмотрим более подробно процесс линеаризации для каждого вида зависимости. Пусть дана выборка x1,y1 , x2,y2 ,..., xn,yn . Наша задача за-

ключается в построении эмпирического уравнения регрессии по этим данным, т.е. в получении наилучших оценок a и b для теоретических параметров и .

Логарифмическая регрессия y ln x .

Линеаризация производится путем замены x lnx (здесь и всюду далее штрих играет роль метки и не связан с дифференцированием). Это приводит к тому, что исходная выборка заменяется новой выборкойx1,y1 , x2,y2 ,..., xn, yn , где xi ln xi и исходное уравнение становится

линейным:

y x .

34

Его параметры могут быть оценены по выборке xi ,yi с помощью

МНК для линейной регрессии, т.е. по формулам

b cov(X ,Y), a y bx .

Dx

В результате получим эмпирическое уравнение регрессии

y* a bln x.

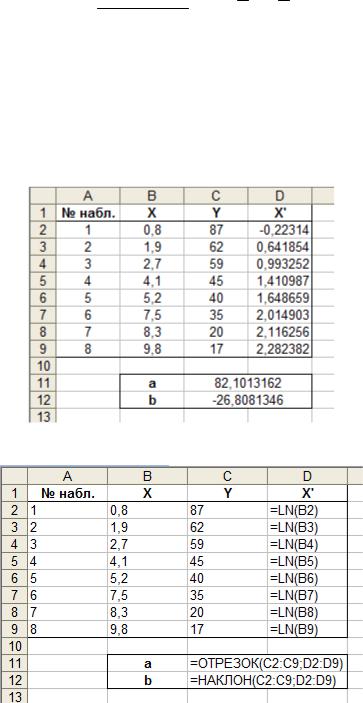
Пример 8. Построим логарифмическую регрессию для выборки из примера 1. Для этого необходимо перейти от выборки (X,Y) к линеаризованной выборке (X,Y') и получить для нее каким либо способом (см. пример 4) коэффициенты линейной регрессии. Расчеты представлены на рисунках 3.1 и 3.2.

Рис. 3.1. Расчет коэффициентов логарифмической регрессии

Рис. 3.2. Формулы для расчета коэффициентов логарифмической регрессии

Таким образом, логарифмическая регрессия для выборки из примера 1 имеет

вид y* 82,1 26,81ln x.

35

линейным:

y x .

Его параметры могут быть оценены по выборке xi ,yi с помощью

МНК для линейной регрессии, т.е. по формулам

b cov(X ,Y), a y bx .

Dx

В результате получим эмпирическое уравнение

y* a b . x

Степенная регрессия y x .

Эта модель относится к моделям нелинейным по параметрам. Линеаризация производится путем логарифмирования обеих частей уравнения:

ln y ln( x ),

ln y ln ln x ln .

x1,y1 , x2,y2 ,..., xn, yn , где yi ln yi , xi ln xi .

Параметры уравнения могут быть оценены по выборке xi ,yi с по-

мощью МНК для линейной регрессии, т.е. по формулам

b cov(X ,Y ) , c y bx (c – оценка для ).

Dx

В результате получим эмпирическое уравнение

ln y* c blnx.

После потенцирования будем иметь

eln y* eceblnx.

Наконец, вводя обозначение a ec , приходим к уравнению

36

y* axb.

Пример 9. Построим степенную регрессию для выборки из примера 1. Для этого необходимо перейти от выборки (X,Y) к линеаризованной выборке (X',Y') и получить для нее каким либо способом (см. пример 4) коэффициенты линейной регрессии, тем самым мы получим c и b. Затем из с получим a. Расчеты представлены на рисун-

ках 3.3 и 3.4.

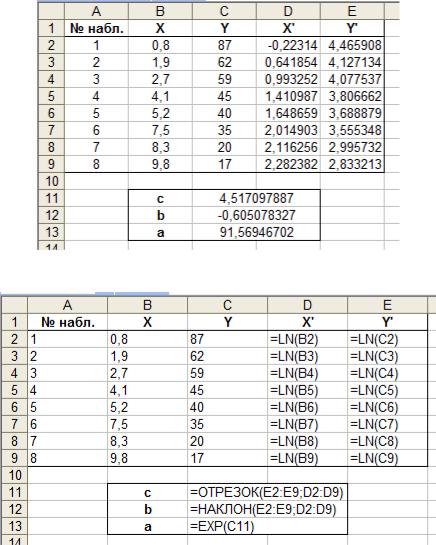
Рис. 3.3. Расчет коэффициентов степенной регрессии

Рис. 3.4. Формулы для расчета коэффициентов степенной регрессии

Таким образом, степенная регрессия для выборки из примера 1 имеет вид

y* 91,57 x 0,61.

Экспоненциальная регрессия y x .

Линеаризация производится путем логарифмирования обеих частей уравнения:

ln y ln( x ),

37

ln y ln xln ln .

После выполнения замены ln , y ln y, ln , ln получа-

ем линейное уравнение

y x .

При этом исходная выборка заменяется новой выборкой

x1,y1 , x2,y2 ,..., xn, yn , где yi ln yi .

Параметры уравнения могут быть оценены по выборке xi ,yi с по-

мощью МНК для линейной регрессии, т.е. по формулам

d cov(X,Y ), c y bx (c – оценка для , d – оценка для ).

Dx

В результате получим эмпирическое уравнение

ln y* c dx.

После потенцирования будем иметь

eln y* ecedx .

Наконец, вводя обозначение a ec , b ed приходим к уравнению

y* abx.

3.3. Выбор нелинейной зависимости

В случае парной регрессии выбор вида зависимости обычно осуществляется по графическому изображению реальных статистических данных в виде точек, которое называется корреляционным полем. Для того, чтобы по корреляционному полю подобрать вид зависимость, необходимо знать, как выглядит ее график. Приведем изображения графиков зависимостей, которые были рассмотрены выше.

38

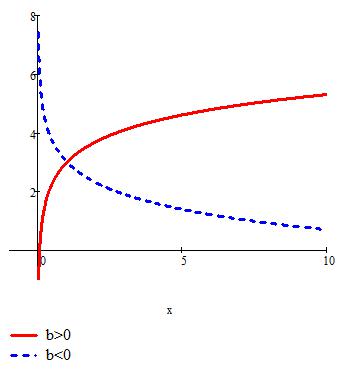
Логарифмическая зависимость.

Рис. 3.5. График логарифмической зависимости y a bln x

Свойства логарифмической зависимости существенно зависят от знака коэффициента b. Если b 0, то логарифмическая функция возрастает и выпукла вверх, а если b 0, то убывает и выпукла вниз.

39

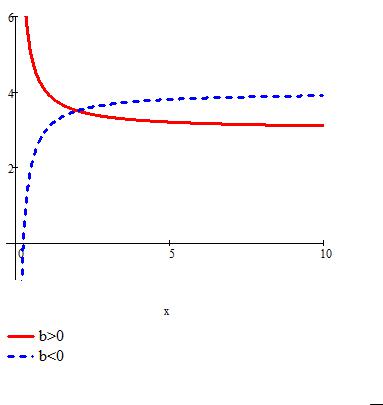
Гиперболическая зависимость.

Рис. 3.6. График гиперболической зависимости y a b

x

Свойства гиперболической зависимости существенно зависят от знака коэффициента b. Если b 0, то гиперболическая функция возрастает и выпукла вверх, а если b 0, то убывает и выпукла вниз.

40