Эконометрика. Учебное пособие

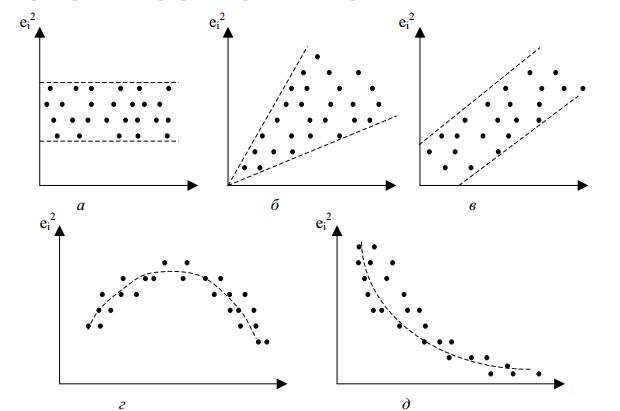
мощи визуального анализа. Для этого удобно анализировать графики квадратов остатков.

На рисунке 4.10 приведены некоторые возможные ситуации.

Рис. 4.10. Визуальный анализ квадратов остатков: а) – гомоскедастичные остатки; б)-д)

– гетероскедастичные остатки

Тест Голдфелда-Квандта. Наиболее популярным формальным критерием является критерий, предложенный С. Голдфелдом и Р. Квандтом. При проведении проверки по этому критерию предполагается, что стандартное отклонение пропорционально значению одной из факторных переменных в

этом наблюдении. Предполагается также, что случайный член распределен нормально и не подвержен автокорреляции.

Тест Голдфелда-Квандта – тест на гетероскедастичность, устанавливающий, что стандартное отклонение остаточного члена регрессии растет, когда растет объясняющая переменная.

Все наблюдений в выборке упорядочиваются по величине z, после чего оцениваются отдельные регрессии для первых m и для последних m наблюде-

ний; средние n 2m наблюдений отбрасываются. Если предположение о ге-

тероскедастичности верно, то дисперсия в последних m наблюдениях будет больше, чем в первых m, и это будет отражено в сумме квадратов остатков в двух указанных частных регрессиях.

71

Обозначая суммы квадратов остатков в регрессиях для первых m и по-

ост

m k 1 степенями свободы, где k – число объясняющих переменных в

регрессионном уравнении. Если данное значение превышает критическое зна-

чение F m k 1,m k 1 , то нулевая гипотеза об отсутствии гетероскеда-

стичности отклоняется.

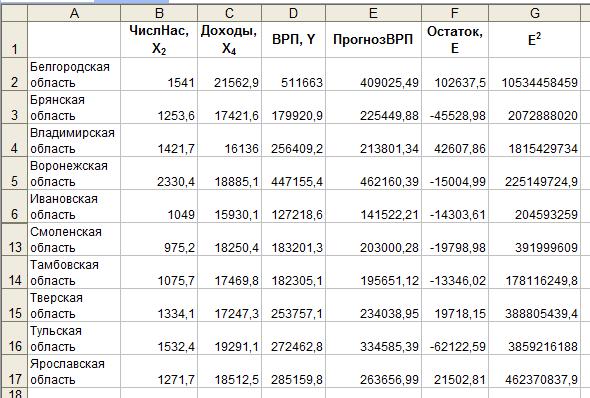
Пример 14. Проведем анализ остатков уравнения, полученного в примере 13. Вычисление остатков представлено на рисунках 4.11 и 4.12.

Рис. 4.11. Расчет остатков (ячейки 7-12 скрыты)

72

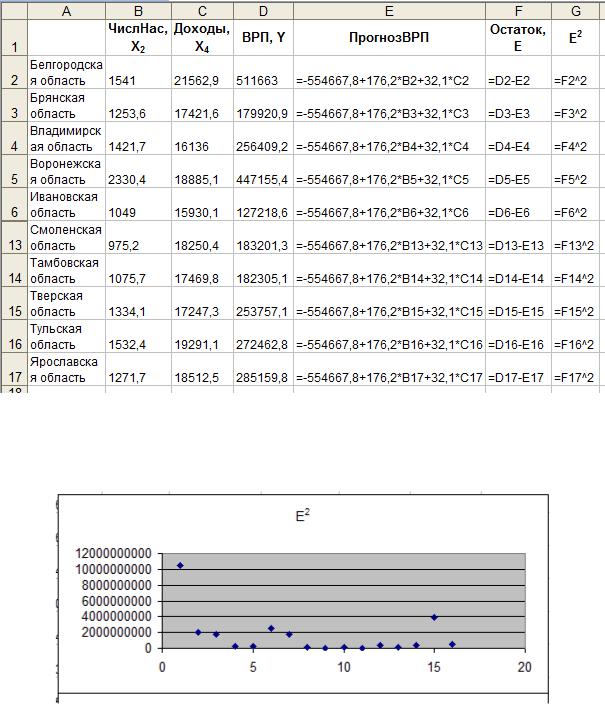
Рис. 4.12. Формулы для расчета остатков (ячейки 7-12 скрыты)

График квадратов остатков представлен на рисунке 4.13 (построение: Диа-

граммы=>Точечная).

Рис. 4.13. Графики остатков и квадратов остатков

Сделать сколь-нибудь достоверные выводы о гомоскедастичности по этому рисунку нельзя, потому что точек на диаграмме слишком мало. С другой стороны, диаграммы показывают, что явной, ярко выраженной гетероскедастичности здесь тоже нет.

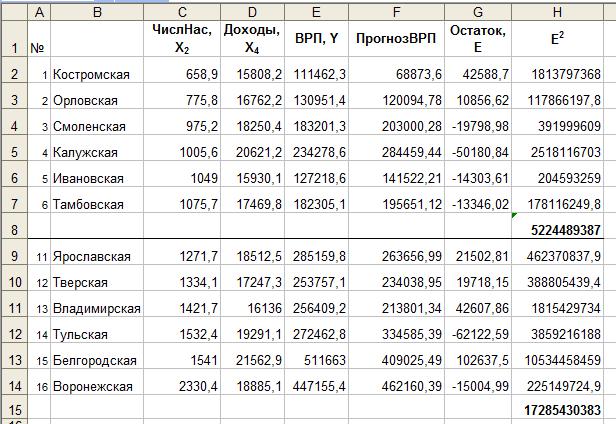
Продемонстрируем использование критерия Голдфелда-Квандта. Проверим наличие (отсутствие) зависимости между переменной X2 и отклонением остатков, для чего упорядочим данные по переменной X2 (инструмент Сортировка). Для m=6 расчеты представлены на рисунке 4.14.

73

сутствии гетероскедастичности остатков нет.

74

5. Временные ряды. Основные понятия

Эконометрическую модель можно построить, используя два типа исходных данных:

Данные, характеризующие совокупность различных объектов в определенный момент (период) времени;

Данные, характеризующие один объект за ряд последовательных моментов (периодов) времени.

Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные по данным второго типа, назы-

ваются моделями временных рядов.

Временной ряд – совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени (значения показателя называют уровнями ряда). Временные ряды также называют динамиче-

скими рядами или рядами динамики.

Примеры временных рядов: динамика курса валюты за некоторый период, ежемесячная прибыль предприятия за год, статистика по ежедневным продажам какого-либо товара за месяц и т.д.

5.1. Аддитивная и мультипликативная модели временного ряда

Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:

Факторы, формирующие тенденцию ряда; Факторы, формирующие циклические колебания ряда; Случайные факторы.

При различных сочетаниях этих факторов зависимость уровней ряда от времени может принимать разные формы.

Во-первых, большинство временных рядов экономических показателей имеют тенденцию, характеризующую совокупное долговременное воздействие множества факторов на динамику изучаемого показателя. По всей видимости, эти факторы, взятые в отдельности, могут оказывать разнонаправленное воздействие на исследуемый показатель. Однако в совокупности они формируют его возрастающую или убывающую тенденцию.

Во-вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезонный характер, поскольку экономическая деятельность ряда отраслей зависит от времени года (например, цены на сельскохозяйственную продукцию в летний период выше, чем в зимний; уровень безработицы в курортных городах в зимний период выше по сравнению с летним). При наличии больших массивов данных за длительные промежутки времени можно выявить циклические колебания, связанные с общей динамикой конъюнктуры рынка, а также с фазой бизнес-цикла, в которой находится экономика страны.

75

Некоторые временные ряды не содержат тенденцию и циклическую компоненту, а каждый следующий их уровень образуется как сумма среднего уровня ряда и некоторой (положительной или отрицательной) случайной компоненты.

Чаще всего модели содержат все три компоненты. Каждый их уровень формируется под воздействием тенденции, сезонных колебаний и случайной компоненты.

В большинстве случаев фактический уровень временного ряда можно представить как сумму трендовой, циклической и случайной компонент

Y T S E,

где T – тенденция, S – сезонная компонента, E – случайная компонента. Такая модель называется аддитивной моделью временного ряда.

Также, в некоторых случаях, уровень временного ряда может быть представлен как произведение перечисленных компонент, т.е.

Y T S E.

Такая модель называется мультипликативной моделью временного ря-

да.

Выбор одной из этих моделей основывается на анализе структуры временного ряда. Если амплитуда сезонных колебаний примерно постоянна, то строят аддитивную модель. Если же амплитуда колебаний непостоянна, то есть возрастает или уменьшается, то строят мультипликативную модель.

Основная задача эконометрического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент, с тем чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.

5.2. Коэффициент автокорреляции. Коррелограмма

Между значениями временного ряда может иметь место корреляционная

связь.

Автокорреляция уровней временного ряда – корреляционная связь между последовательными уровнями одного и того же ряда, сдвинутыми на определенный промежуток времени , который называется лагом. То есть, автокорреляция – это корреляционная связь между рядами

y1,y2 ,yn и y1 ,y2 ,yn .

Автокорреляция может быть измерена с помощью коэффициента автокорреляции (сокр. КА), который рассчитывается по стандартной формуле для коэффициента корреляции

St St

где

76

y1,y2 ,yn , соответственно.

Лаг (сдвиг во времени) определяет порядок коэффициента автокорреляции. Если 1, то говорят об автокорреляции первого порядка. При этом r1

называют коэффициентом автокорреляции 1-ого порядка. Если 2, то говорят о коэффициенте автокорреляции 2-ого порядка и т.д. Здесь следует обратить внимание, что с увеличением лага на единицу, число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается на 1. Поэтому обычно не рассматривают коэффициенты автокорреляции порядка большего, чем n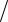4, где n – длинна ряда.

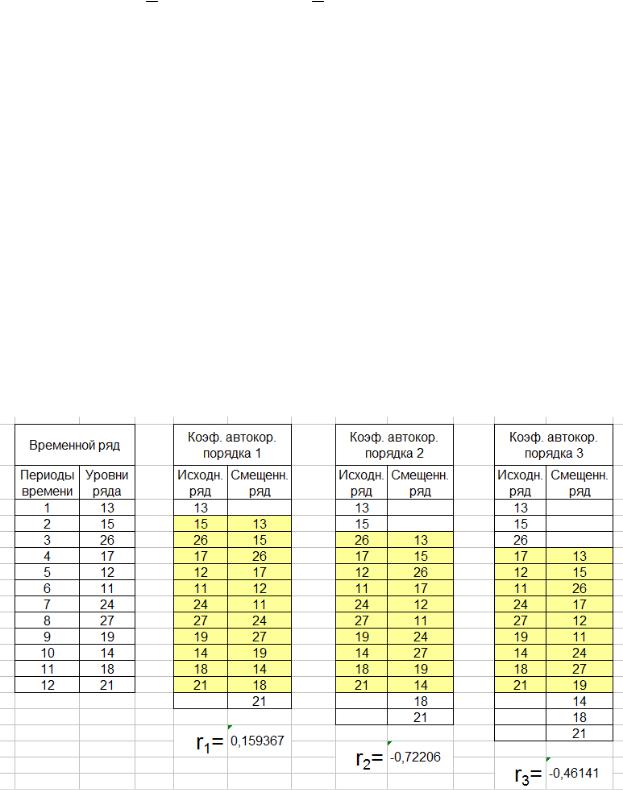
В программе Microsoft Excel коэффициент автокорреляции можно вычислить с помощью встроенной функции КОРРЕЛ(Диап1;Диап2), где Диап1, Диап2 – диапазоны ячеек, содержащие ряды y1 ,y2 ,yn и y1,y2 ,yn . Вычисление коэффициента автокорреляции наглядно представлено на рисунках

5.1 и 5.2.

Рис. 5.1. Вычисление коэффициентов автокорреляции различных порядков

77

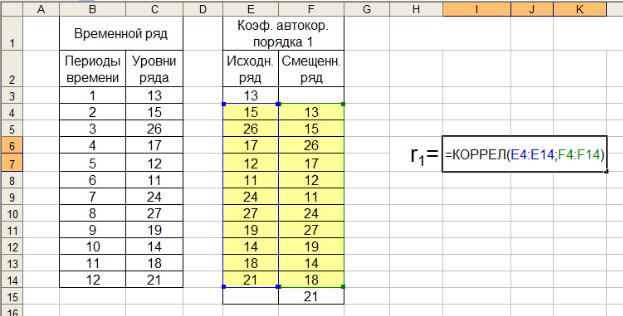
Рис. 5.2. Формула для расчета коэффициента автокорреляции первого порядка

Поскольку для каждого лага может быть вычислено значение коэффициента автокорреляции, то мы получаем зависимость между лагом и коэффициентом автокорреляции, которая называется автокорреляционной функцией. График этой функции называют коррелограммой.

Коррелограммой удобно пользоваться для отыскания лагов, при которых автокорреляция наиболее высокая. Тем самым можно выявить структуру временного ряда. Если исследуемый ряд содержит линейную тенденцию, то коэффициент автокорреляции первого порядка должен быть достаточно большим, т.е. значимо отличаться от нуля. Однако он может быть большим и для ряда, который не содержит тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка , то ряд содержит колебания с периодом τ. Если ни один из коэффициентов автокорреляции не является значимым, то можно сделать одно из двух предположений:

Ряд не содержит тенденции и циклических колебаний, а его уровень определяется только случайной компонентой;

Ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.

Использование коррелограммы продемонстрируем на примерах.

Пример 15. На рисунке 5.3 изображены объемы внешней торговли РФ со странами СНГ за 2009-2013г. и коррелограмма этого временного ряда. Острый пик коррелограммы при =12 означает наличие циклической составляющей с периодом 12 месяцев. Высокое значение коэффициента автокорреляции первого порядка говорит о том, что возможно ряд имеет линейную тенденцию (вид диаграммы временного ряда подтверждает наличие возрастающей тенденции).

78

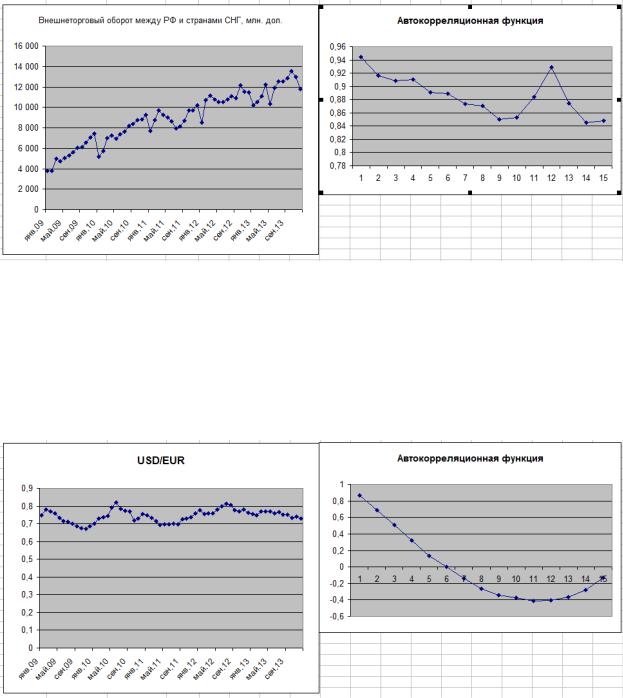
Рис. 5.3. Внешнеторговый оборот между РФ и странами СНГ

Пример 16. Рассмотрим валютный курс пары USD/EUR за период 2009-2013г (рис. 5.4). Из вида коррелограммы следует, что данный ряд не имеет циклической составляющей. Высокое значение коэффициента автокорреляции первого порядка говорит о том, что возможно ряд имеет линейную тенденцию, однако диаграмма временного ряда свидетельствует об обратном (возможно тенденция есть, но очень незначительная).

Рис. 5.4. Курс USD/EUR

Пример 17. Коррелограмма для среднемесячной температуры воздуха показывает наличие циклической составляющей с периодом 12 месяцев (рис. 5.5).

79

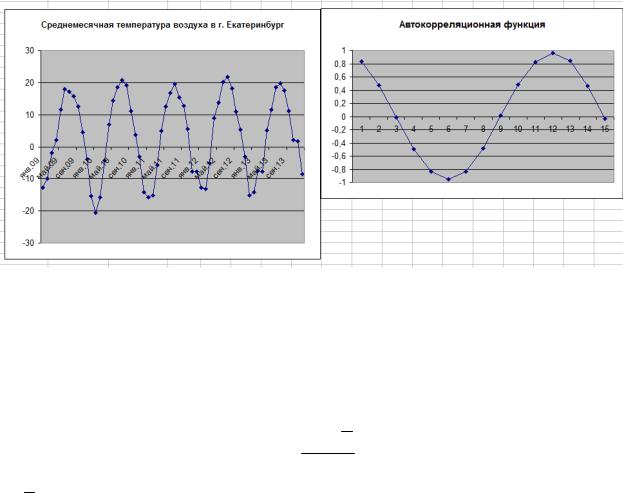
Рис. 5.5. Среднемесячная температура воздуха

Чтобы понять, почему коэффициент автокорреляции первого порядка может быть большим при отсутствии тренда, необходимо проанализировать формулу, по которой он вычисляется. Для этого удобно от исходного ряда yt

перейти к нормированному и центрированному ряду, т.е. выполнить линейную замену

zt yt y , Sy

где y – средний уровень ряда, Sy – среднее квадратичное отклонение ряда.

Коэффициент автокорреляции первого порядка для ряда zt имеет вид

Таким образом, r1 равно сумме произведений соседних уровней. Если смена знака уровней ряда zt происходит редко, то это означает, что соседние уровни в большинстве случаев будут иметь одинаковый знак. Следовательно, большинство слагаемых в r1 будет положительным, и r1 будет большим. Такой

ряд называют рядом с долгопериодическими колебаниями. Продолжая ана-

лиз, можно отметить, что в случае, когда уровни ряда меняют знак так же часто, как не меняют, отрицательных и положительных слагаемых в r1 будет пример-

но поровну и, следовательно, r1 будет малым. Если смена знака происходит на-

много чаще, чем «несмена», то отрицательных слагаемых будет больше и r1 бу-

дет близок к -1.

Пример 18. Примером временного ряда с малым коэффициентом автокорреляции первого порядка может служить ряд, уровни которого суть изменения валютного курса, то есть разности между курсами двух последовательных периодов (рис. 5.6).

80