Правило кільця

Нехай дано алгебраїчне рівняння

,

де – дійсні коефіцієнти і нехай ,.

Тоді корені рівняння розташовані в круговому кільці, де

; .

П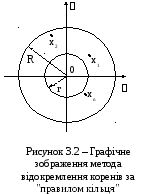ри цьому r – нижня, а R – верхня границя додатних коренів алгебраїчного рівняння і – відповідно нижня і верхня границя від’ємних коренів (рис. 3.2).

Метод Ньютона

Якщо при x = c многочлен і його похідні приймають додатні значення, то с є верхньою границею додатних коренів рівняння .

5. Методи розв’язання нелінійних рівнянь

Метод бісекції (половинного ділення)

В результаті відокремлення коренів нелінійного рівняння стає відомим відрізок [a, b], на якому знаходиться тільки один корінь рівняння f (x) = 0, причому на цьому відрізку функція неперервна і значення функції на кінцях відрізку мають різні знаки.

Метод бісекції полягає у тому, що в кожному наступному наближенні за корінь приймають значення х в середині відрізку (рис. 3.3).

Після першої ітерації (розділення відрізку навпіл) визначають, на якій з половин відрізку міняється знак функції. Саме цю частину вибирають для подальших уточнень.

Ітерації проводять до тих пір, поки відстань між кінцями відрізку не стає меншою за задану абсолютну похибку.

Метод бісекції є повільним, однак збіжність його гарантована.

Метод хорд

Для пошуку кореня на відрізку х[a,b], за умов описаних вище, кожним наступним наближенням кореня є точка перетину відрізка, що з’єднує значення функції на кінцях відрізку (перша ітерації – f(а) і f(b)), – хорди, з віссю х (рис. 3.4). Причому кожен раз значення функції на кінцях відрізку повинні мати різний знак. Ітерації проводять до тих пір, поки відстань між кінцями відрізку не стане меншою за задану похибку.

Значення х для кожної наступної ітерації визначають з рівняння хорди , де а і b – кінці відрізку на кожній ітерації.

Метод дотичних (метод Ньютона)

Даний метод полягає у заміні функції f(х) = 0 її дотичною в кінці відрізка [а,b], отриманого за умов описаних вище.

В кожній наступній ітерації за корінь приймаємо значення абсциси перетину дотичної з віссю х (рис. 3.5). Розрахункова формула, для визначення точки перетину записується .

Ітераційний процес припиняється за умов зменшення відстані між результатами послідовних ітерації менше за задану похибку.

Особливістю такого методу є необхідність визначення похідної функції f(х). Метод дотичних результат з достатньою точністю після невеликої кількості ітерацій, але його недоліком є те, що для гарантованої збіжності необхідно вибирати правильне початкове наближення (достатньо близьке). Тому на практиці при розробці програм для ЕОМ поєднують метод дотичних із більш стійкими методами, наприклад, методом бісекції.

Метод простих ітерацій

Для використання такого методу необхідно функцію перетворити до ітераційного вигляду х = (х).

Кожна наступна ітерація розраховується за формулою . Ітераційний процес припиняється за умов зменшення відстані між результатами послідовних ітерації менше за задану похибку.

Не кожне рівняння можна розв’язати методом простих ітерацій, тому що ітераційний процес може бути збіжним або розбіжним. Збіжність ітераційного процесу залежить від величини похідної ітераційної функції (див. рис. 3.6). Умовою збіжності ітерацій є .

Ітераційні методи стійкі до помилки, допущеної на одній з ітерацій, але за умови використання комп’ютерного розрахунку похибка, якщо вона є, повторюватиметься на всіх ітераціях. При цьому погіршуватиметься якість розв’язання. Зараз широко використовуються комбіновані методи, в яких поєднано швидкі ітераційні методи із надійними методами бісекції і хорд.

6. Методи розв’язання систем нелінійних рівнянь

Систему нелінійних рівнянь (СНР) можна представити у вигляді

. (3.2)

На відміну від систем лінійних рівнянь для СНР не існує точних методів розв’язання. Лише дуже обмежену кількість систем можна вирішити безпосередньо. Наприклад, систему з двох рівнянь можна розв’язати графоаналітичним методом або можна одну невідому виразити через іншу і потім розв’язати відносно одної невідомої. Але абсолютну більшість систем вирішують ітераційними методами.

Метод простих ітерацій розв’язання СНР

Даний метод є розвитком методу простих ітерацій для нелінійного рівняння. Суть метода полягає у представленні системи рівнянь у ітераційному вигляді

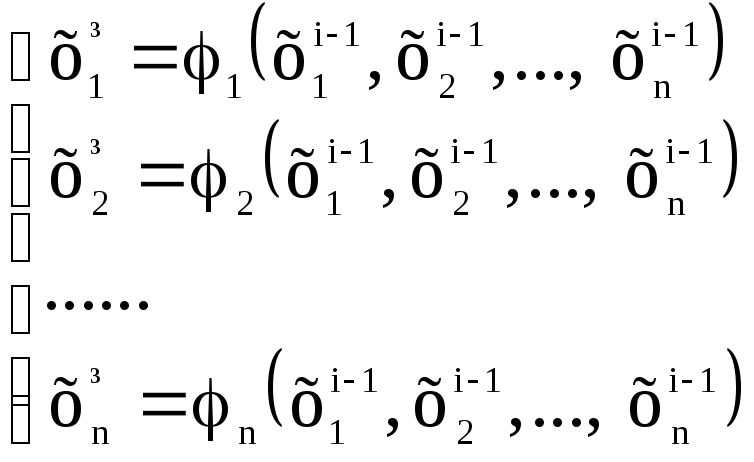. (3.3)

Далі така система нелінійних рівнянь розв’язується послідовними наближеннями. Збіжність системи рівнянь забезпечується за умови, що модулі похідних всіх ітераційних функцій в заданому діапазоні не перевищують 1. Недоліком даного методу є погана збіжність, ускладнення при виборі вигляду ітераційних функцій, велика кількість ітерацій, необхідність достатньо точного задавання початкових наближень.

Метод Ньютона розв’язання СНР

Для системи рівнянь (3.2) є певне наближення розв’язку

. (3.4)

Тоді точне значення розв’язку можна записати

. (3.5)

Тоді рівняння можна записати, розклавши його в ряд Тейлора і заливши тільки члени першого порядку

. (3.6)

Далі використовуючи обернену матрицю Якобі – матрицю кінцевих похідних W отримаємо кінцевий ітераційний вираз

. (3.7)

Метод Ньютона має набагато кращу збіжність і меншу кількість ітерацій. Недоліком даного методу є необхідність визначення похідних функцій, що не завжди можна зробити точними методами.

Метод збурення параметрів

Це ітераційний метод, суть якого полягає у такому. Систему нелінійних рівнянь замінюють на таку систему рівнянь, розв’язок якої відомий. Потім поступово змінюючи вигляд функцій за допомогою кінцевого числа послідовних наближень параметрів отримуємо шукану систему рівнянь.

Перевагою такого методу є те, що не вимагається достатньо точних перших наближень. Недоліком такого методу є необхідність проведення великої кількості ітераційних розрахунків і, відповідно, використання великої кількості комп’ютерного часу.

7. Розв’язання систем нелінійних рівнянь з використанням пакетів прикладних програм

Одним з найзручніших математичних пакетів прикладних програм для розв’язання систем нелінійних рівнянь є Mathcad.

В середовищі Mathcad запрограмоване розв’язання СНР. Для цього використовується мітка Given, яка вказує на початок запису системи рівнянь і оператор Find (x₁ , х₂ , …), який записується нижче системи рівнянь і повертає корені системи рівнянь. Нелінійні рівняння записуються із використанням символьного знаку рівності (Сtrl+).

Для коректного розв’язання системи рівнянь в Mathcad на початку необхідно задати початкові наближення для всіх величин, що використовуються в системі рівнянь.

Далі наведений приклад розв’язання системи з 4 нелінійних рівнянь для розрахунку показників потоку води в трубопроводі (рис. 3.7).

Контрольні запитання

1. Поясніть класифікацію нелінійних рівнянь.

2. Поясніть методи визначення кількості коренів нелінійних рівнянь.

3. Поясніть методи відокремлення коренів нелінійних рівнянь.

4. Поясніть метод бісекції розв’язання нелінійних рівнянь.

5. Поясніть метод хорд розв’язання нелінійних рівнянь.

6. Поясніть метод дотичних (метод Ньютона) розв’язання нелінійних рівнянь.

7. Поясніть метод простих ітерацій розв’язання нелінійних рівнянь.

8. Поясніть умови збіжності ітераційного процесу розв’язання нелінійних рівнянь.

9. Дайте характеристику системи нелінійних рівнянь.

10. Поясніть метод простих ітерацій розв’язання систем нелінійних рівнянь.

11. Поясніть метод Ньютона розв’язання систем нелінійних рівнянь.

12. Поясніть метод збурення параметрів розв’язання систем нелінійних рівнянь.

13. Поясніть особливості розв’язання систем нелінійних рівнянь з використанням пакету прикладних програм Mathcad.

Приклади розв’язання задач

Приклад 3.1. Визначити кількість додатних та від’ємних коренів рівняння .

Розв’язання

Згідно з основною теоремою алгебри це рівняння має чотири корені. Рівняння є повним, послідовність знаків коефіцієнтів така: +, – , +, +, – . Знак змінюється два рази. Отже, додатних коренів або 2, або жодного. Кількість сталостей знака дорівнює 1. Отже, дане рівняння має один від’ємний корінь.

Приклад 3.2. Відокремити корені нелінійного рівняння за правилом кільця.

Розв’язання

Для такого рівняння ,. Тоді,.

Тобто для цього рівняння корені, якщо вони існують, знаходяться в діапазоні х: дійсні – х  [-12; 12]; додатні х  [0,431; 12]; від’ємні х  [-12; -0,431].

Приклад 3.3. Методом Ньютона визначити верхню границю додатних коренів рівняння .

Розв’язання

Знаходимо ,,,.

Перевірці підлягають значення x > 0. При х = 1 маємо ,,. Отже, проводити далі перевірку для х = 1 не потрібно. Перевіримо значення х = 2.,,,,. Таким чином, верхньою границею додатних коренів є число 2, тобто R = 2. За нижню границю можна взяти число, обернене до R, тобто r = 1/2.

Приклад 3.4. В результаті запису рівняння Дарсі для потоку рідини в каналі отримане рівняння залежності втрат тиску від швидкості w потоку

. Визначити корінь такого нелінійного рівняння методом бісекції, якщо Па з похибкою не більше 1%.

Розв’язання

Спростимо рівняння, запишемо швидкість через х

.

Використовуючи "правило кільця" отримаємо, що додатній корінь цього рівняння знаходиться в діапазоні х[0,166; 1,2].

Визначимо функцію на кінцях діапазону , . Бачимо, що функція міняє знак.

Нульова ітерація х₀ = (0,166+1,2)/2=0,683, . Функція міняє знак на частині діапазону х₁[0,166; 0,683], тому шукаємо корінь в цьому діапазоні. Наступні ітерації проводимо аналогічно: 1) х₁ = 0,425, х₂[0,166; 0,425]; 2) х₂ = 0,295, х₂[0,295; 0,425] і так далі.

На сьомій і восьмій ітерації х₇ = 0,400, х₈ = 0,397 і похибка . Розрахунок завершено.

Приклад 3.5. Визначити корінь нелінійного рівняння з попереднього прикладу методом хорд на відрізку [0,166; 1,2] з похибкою не більше 1%.

Розв’язання

Значення функції на кінцях відрізку f(0,166) = -0,819, f(1,2) = 7,576.

Перша ітерація , f(0,267) = –0,545, і т.д.

Після сьомої ітерації х₇ = 0,398, похибка при цьому складає 0,55%.

Приклад 3.6. Визначити корінь нелінійного рівняння з попередніх прикладів методом дотичних на відрізку [0,166; 1,2] з похибкою до 1%.

Розв’язання

Похідна функції , значення функції f(0,166) =  = -0,819, f(1,2) = 7,576. Починаємо ітераційний процес зх₀ = 1,2, . Перша ітерація, х₂ = 0,449, х₃ = 0,402, х₄ = 0,399. Після четвертої ітерації похибка не перевищує 0,65%.

Приклад 3.7. Визначити корінь нелінійного рівняння з попередніх прикладів методом простих ітерацій на відрізку [0,166; 1,2].

Розв’язання

Перетворимо функцію до ітераційного вигляду. Маємо два варіанти перетворення:або.

Для виявлення збіжності ітерацій знайдемо похідну обох функцій. Отримаємо відповідно та.

Похідна ітераційної функції при х = 0,166 приймає значення -1,01, а при х = 1,2 не може бути розрахована через від’ємний підкореневий вираз. Очевидно, що такий ітераційний процес буде розбіжним.

Похідна ітераційної функції в діапазоні х = 0,166…0,85 має значення -1 <'(x) < 0, а далі різко зростає. Тому в цьому діапазоні значень х ітераційний процес буде збіжним.

Приймаємо х₀ = 0,166, тоді ,і так далі.

На четвертій ітерації х₄ = 0,399 і похибка не перевищує 0,58%.

Задачі для самостійної роботи

Приклад 3.8. Визначити кількість та відокремити корені нелінійного рівняння за "правилом кільця"

Варіант 1 2х4 – х3 + 4х2 + 8х – 20 = 0	Варіант 2 25х4 + 12х3 – 18х2 + 2х – 3 = 0
Варіант 3 2х4 – 3х3 – 3х2 – 4х – 8 = 0	Варіант 4 –3х4 + 2х3 + х2 – 4х + 2 = 0
Варіант 5 4х4 – 9х3 + 12х2 – 8х – 5 = 0	Варіант 6 х4 + х3 – 2х2 + 2х – 2 = 0
Варіант 7 -5х4 – 5х3 + 2х2 – 2х + 12 = 0	Варіант 8 3х4 – 9х3 + 12х2 – 2х – 12 = 0

Приклад 3.9. Визначити корінь нелінійного рівняння методом бісекції, хорд, дотичних та методом простих ітерацій з похибкою до 1%.

Варіант 1 2х4 – х3 + 4х2 + 8х – 20 = 0	Варіант 2 25х4 + 12х3 – 18х2 + 2х – 3 = 0
Варіант 3 2х4 – 3х3 – 3х2 – 4х – 8 = 0	Варіант 4 –3х4 + 2х3 + х2 – 4х + 2 = 0
Варіант 5 4х4 – 9х3 + 12х2 – 8х – 5 = 0	Варіант 6 х4 + х3 – 2х2 + 2х – 2 = 0
Варіант 7 -5х4 – 5х3 + 2х2 – 2х + 12 = 0	Варіант 8 3х4 – 9х3 + 12х2 – 2х – 12 = 0

Приклад 3.10. Скласти та розв’язати систему нелінійних рівнянь з використанням Mathcad для такого завдання. Дві посудини зв’язані трубопроводом довжиною 50 м. Вода з густиною 990 кг/м³ перетікає з однієї до іншої посудини з сталими рівнями самопливом. Необхідна витрата води 12 кг/с. Шорсткість труб 0,3 мм. Сума місцевих опорів лінії складає 10. Діаметр труби 100 мм. Середня в’язкість води 0,8  10^-6 м²/с. Визначити необхідну різницю висот між рівнями рідини в посудинах. Швидкість води в трубі, коефіцієнт опору тертя, втрати тиску в контурі.