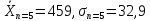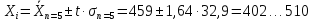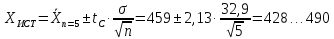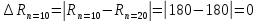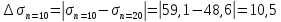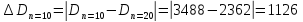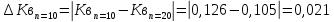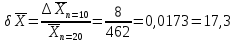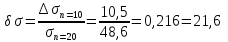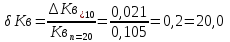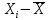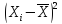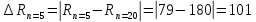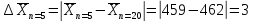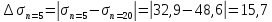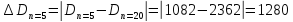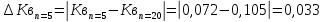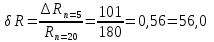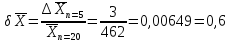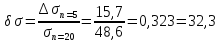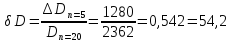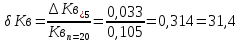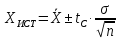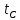- •Оглавление
- •Тема №1. Основные статистические характеристики выборки результатов измерений. Классификация измерений.
- •Расчет.
- •Тема №2. Оценка влияния объема выборки на основные статистические характеристики.
- •Расчет.
- •Расчет.
- •Тема №3. Интервальная оценка результатов измерений.
- •Тема №4. Исключение из выборки результатов, содержащие грубые погрешности.
- •Тема №5. Планирование статистического контроля качества дорожно-строительных работ.
- •Тема № 6: Проверка соответствия экспериментальных данных нормальному закону распределения случайной величины.
- •Список используемой литературы.
Оглавление
Тема №1. Основные статистические характеристики выборки результатов измерений. Классификация измерений. 3
Тема №2. Оценка влияния объема выборки на основные статистические характеристики. 4
Тема №3. Интервальная оценка результатов измерений. 8
Тема №4. Исключение из выборки результатов, содержащие грубые погрешности. 11
Тема №5. Планирование статистического контроля качества дорожно-строительных работ. 14
Тема № 6: Проверка соответствия экспериментальных данных нормальному закону распределения случайной величины. 18
Список используемой литературы. 25
Тема №1. Основные статистические характеристики выборки результатов измерений. Классификация измерений.
|
№ измерения i |
Результат измерения Xi |
|
|
|
1 |
515 |
53 |
2809 |
|
2 |
443 |
-19 |
361 |
|
3 |
526 |
64 |
4096 |
|
4 |
425 |
-37 |
1369 |
|
5 |
404 |
-58 |
3364 |
|
6 |
432 |
-30 |
900 |
|
7 |
512 |
50 |
2500 |
|
8 |
515 |
53 |
2809 |
|
9 |
449 |
-13 |
169 |
|
10 |
473 |
11 |
121 |
|
11 |
414 |
-48 |
2304 |
|
12 |
437 |
-25 |
625 |
|
13 |
459 |
-3 |
9 |
|
14 |
438 |
-24 |
576 |
|
15 |
377 |
-85 |
7225 |
|
16 |
460 |
-2 |
4 |
|
17 |
557 |
95 |
9025 |
|
18 |
511 |
49 |
2401 |
|
19 |
484 |
22 |
484 |
|
20 |
401 |
-61 |
3721 |
|
|
∑=9232 |
|
∑=44872 |
Расчет.
Размах вариации:
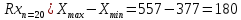
Среднее арифметическое значение:

Среднее квадратичное отклонение:
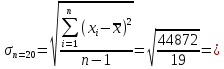 48,597=48,6
48,597=48,6
Дисперсия:
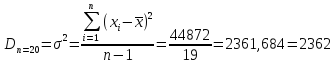
Коэффициент вариации:
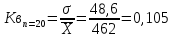
Тема №2. Оценка влияния объема выборки на основные статистические характеристики.
Вариант А: Количество значений в выборке n=10 (i-нечетные):
|
Номер измерения i |
Результат измерения Xi |
|
|
|
1 |
515 |
45 |
2025 |
|
3 |
526 |
56 |
3136 |
|
5 |
404 |
-66 |
4356 |
|
7 |
512 |
42 |
1764 |
|
9 |
449 |
-21 |
441 |
|
11 |
414 |
-56 |
3136 |
|
13 |
459 |
-11 |
121 |
|
15 |
377 |
-93 |
8649 |
|
17 |
557 |
87 |
7569 |
|
19 |
484 |
14 |
196 |
|
|
∑=4697 |
|
∑=31393 |
Расчет.
Размах вариации:
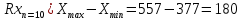
Среднее арифметическое значение:
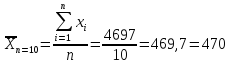
Среднее квадратичное отклонение:
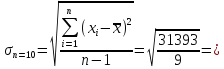 59,060=59,1
59,060=59,1
Дисперсия:
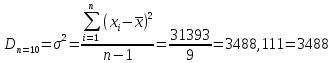
Коэффициент вариации:
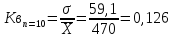
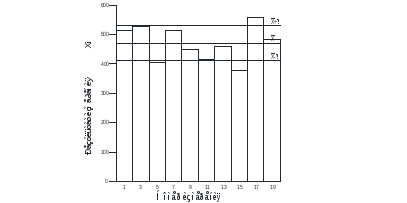
Абсолютные погрешности.
Абсолютные погрешности.
Вывод: При сокращении объема выборки с n=20 до n=10 больше всего изменилось значение дисперсия на 47,7%.
Вариант Б: Количество значений в выборке n=5 (i-2,6,10,14,18):
|
Номер измерения i |
Результат измерения Xi |
|
|
|
2 |
443 |
-16 |
256 |
|
6 |
432 |
-27 |
729 |
|
10 |
473 |
14 |
196 |
|
14 |
438 |
-21 |
441 |
|
18 |
511 |
52 |
2704 |
|
|
∑=2297 |
|
∑=4326 |
Расчет.
Размах вариации:
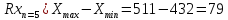
Среднее арифметическое значение:
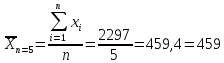
Среднее квадратичное отклонение:
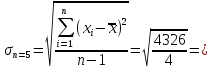 32,886=32,9
32,886=32,9
Дисперсия:
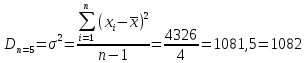
Коэффициент вариации:
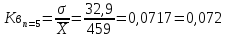
Абсолютные погрешности.
Абсолютные погрешности.
Вывод: При сокращении объема выборки с n=20 до n=5 больше всего изменилось значение размаха на 56,0%.
Тема №3. Интервальная оценка результатов измерений.
Результат измерений – случайная величина (предполагаем)
Доверительная вероятность РДОВ – вероятность попадания случайного результата измерений в (заданный) доверительный интервал.
Доверительный интервал, в котором находится с вероятностью РДОВ случайное значение результата измерения.
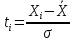 –аргумент функции
Лапласа (коэффициент доверительной
вероятности) показывает расстояние от
–аргумент функции
Лапласа (коэффициент доверительной
вероятности) показывает расстояние от
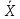 до любой точки.
до любой точки.
Вариант
А: Определить
границы доверительного интервала Xi
для выборки n=20
(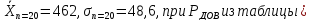
|
РДОВ |
0,683 |
0,954 |
0,997 |
0,70 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
t |
1 |
2 |
3 |
1,04 |
1,28 |
1,44 |
1,64 |
1,96 |
2,58 |
|
РДОВ |
|
t | ||
|
0,683 |
413 |
511 |
1 | |
|
0,954 |
365 |
559 |
2 | |
|
0,997 |
316 |
608 |
3 | |
|
0,70 |
412 |
513 |
1,04 | |
|
0,80 |
400 |
524 |
1,28 | |
|
0,85 |
392 |
532 |
1,44 | |
|
0,90 |
382 |
542 |
1,64 | |
|
0,95 |
367 |
557 |
1,96 | |
|
0,99 |
337 |
587 |
2,58 | |
Вариант
Б: Определить
доверительные границы XИСТ
для выборки n=20
(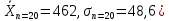
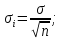

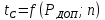 ,коэффициент
Стьюдента берем из таблицы 1,4.
,коэффициент
Стьюдента берем из таблицы 1,4.
|
РДОВ |
|
| ||
|
0,90 |
443 |
481 |
1,73 | |
|
0,95 |
439 |
485 |
2,09 | |
|
0,99 |
431 |
493 |
2,86 | |
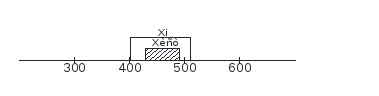
Вариант
В: Определить
доверительные границы Xi
XИСТ
для выборки n=20
(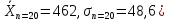 ,
n=10
(
,
n=10
(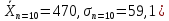 ,
n=5
(
,
n=5
(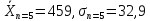 ).
).
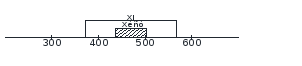
РДОВ=0,9
n=20,
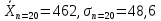
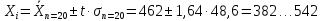
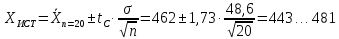

n=10,
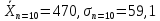
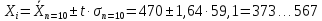
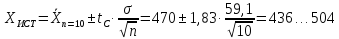
n=5,