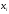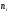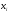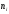Статистическое распределение выборки
Пусть
из генеральной совокупности извлечена
выборка, причем
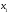 наблюдалось
наблюдалось
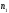 раз,
раз,
 –
–
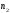 раз,
раз,
 –
–
 раз и
раз и
 – объем выборки. Наблюдаемые значения
– объем выборки. Наблюдаемые значения
 называют вариантами,
а последовательность вариант, записанных
в возрастающем порядке – вариационным
рядом.
Числа наблюдений называют частотами,
а их отношения к объему выборки
называют вариантами,
а последовательность вариант, записанных
в возрастающем порядке – вариационным
рядом.
Числа наблюдений называют частотами,
а их отношения к объему выборки
 – относительными
частотами.
– относительными
частотами.
Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалом и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – соответствие между наблюдаемыми вариантами и их частотами, или относительными частотами.[5]
Пример.
Задано распределение частот выборки
объема
 :
:
|
|
2 |
6 |
12 |
|
|
3 |
10 |
7 |
|
|
|
|
|
Написать распределение относительных частот.
Решение.
Найдем относительные частоты, для чего
разделим частоты на объем выборки:
 ,
,
 ,
,
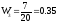 .
.
Напишем распределение относительных частот:
|
|
2 |
6 |
12 |
|
|
0.15 |
0.5 |
0.35 |
Проверка:
 .
[6]
.
[6]
Эмпирическая функция распределения
Пусть
известно статистическое распределение
частот количественного признака
 .
Введем обозначения:
.
Введем обозначения:
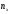 – число наблюдений, при которых
наблюдалось значение признака, меньшее
– число наблюдений, при которых
наблюдалось значение признака, меньшее
 ;
;
 – общее число наблюдений (объем выборки).
Ясно, что относительная частота события
– общее число наблюдений (объем выборки).
Ясно, что относительная частота события
 равна
равна
 .
Если
.
Если
 изменяется, то, вообще говоря, изменяется
и относительная частота, то есть
относительная частота
изменяется, то, вообще говоря, изменяется
и относительная частота, то есть
относительная частота
 есть функция от
есть функция от
 .
Так как эта функция находится эмпирическим
(опытным) путем, то ее называют эмпирической.
.
Так как эта функция находится эмпирическим
(опытным) путем, то ее называют эмпирической.
Эмпирической
функцией распределения
(функцией распределения выборки) называют
функцию
 ,
определяющую для каждого значения
,
определяющую для каждого значения
 относительную частоту события
относительную частоту события
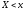 .
[3]
.
[3]
Итак, по определению,
 ,
,
где
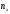 – число вариант, меньших
– число вариант, меньших
 ;
;
 – объем выборки.
– объем выборки.
Таким
образом, для того, чтобы найти, например,
 ,
надо число вариант, меньших
,
надо число вариант, меньших
 ,
разделить на объем выборки:
,
разделить на объем выборки:
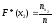 .
.
В
отличие от эмпирической функции
распределения выборки, функцию
распределения
 генеральной совокупности, называют
теоретической
функцией распределения.
Различие между эмпирической и теоретической
функциями состоит в том, что теоретическая
функция
генеральной совокупности, называют
теоретической
функцией распределения.
Различие между эмпирической и теоретической
функциями состоит в том, что теоретическая
функция
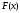 определяет вероятность события
определяет вероятность события
 ,
а эмпирическая функция
,
а эмпирическая функция
 определяет относительную частоту этого
же события. Из теоремы Бернулли следует,
что относительная частота события
определяет относительную частоту этого
же события. Из теоремы Бернулли следует,
что относительная частота события
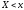 ,
то есть
,
то есть
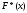 ,
стремится по вероятности, к вероятности
,
стремится по вероятности, к вероятности
 этого события. Другими словами, при
больших
этого события. Другими словами, при
больших
 ,
числа
,
числа
 и
и
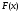 мало отличаются одно от другого, в том
смысле, что
мало отличаются одно от другого, в том
смысле, что
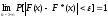 ,
,
 .
Уже отсюда следует целесообразность
использования эмпирической функции
распределения выборки для приближенного
представления теоретической (интегральной)
функции распределения генеральной
совокупности. [3]
.
Уже отсюда следует целесообразность
использования эмпирической функции
распределения выборки для приближенного
представления теоретической (интегральной)
функции распределения генеральной
совокупности. [3]
Такое
заключение подтверждается и тем, что
 обладает всеми свойствами
обладает всеми свойствами
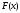 .
Действительно, из определения функции
.
Действительно, из определения функции
 вытекают следующие свойства:
вытекают следующие свойства:
-
значения эмпирической функции принадлежат отрезку
 ;
; -
 – неубывающая
функция;
– неубывающая
функция; -
если
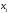 – наименьшая варианта, то
– наименьшая варианта, то
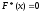 при
при
 ;
если
;
если
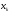 – наибольшая варианта, то
– наибольшая варианта, то
 при
при
 .
.
Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.
Пример. Построить эмпирическую функцию по данному распределению выборки:
|
варианты
|
2 |
6 |
10 |
|
частоты
|
12 |
18 |
30 |
|
|
|
|
|
Решение.
Найдем объем выборки:
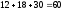 .
Наименьшая варианта равна 2, следовательно,
.
Наименьшая варианта равна 2, следовательно,
 при
при
 .
.
Значение
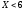 ,
а именно
,
а именно
 ,
наблюдалось 12 раз, следовательно,
,
наблюдалось 12 раз, следовательно,
 ,
при
,
при
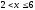 .
.
Значения
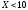 ,
а именно
,
а именно
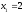 и
и
 ,
наблюдались
,
наблюдались
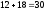 раз, следовательно
раз, следовательно
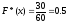 ,
при
,
при
 .
.
Так
как
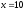 – наибольшая варианта, то
– наибольшая варианта, то
 при
при
 .
.
Искомая
эмпирическая функция: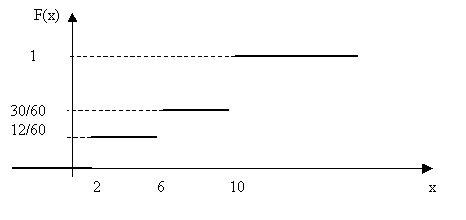
 [6]
[6]