Рівняння неперервності (суцільності) потоку

Нерозривним або суцільним вважають такий потік в якому відсутні пустоти, незаповнені рідиною.

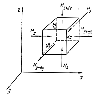Виділимо в середині такого потоку елементарний паралелепіпед об’ємом , де- ребра паралелепіпеда, спрямовані паралельно координатним осям. Нехай складова швидкості на лівій грані площеюдорівнює. Тоді через цю грань в паралелепіпед за одиницю часу ввійде об’єм

.

На протилежній правій грані швидкість і густина можуть відрізнятися і будуть дорівнювати:

і .

Рис. 3.1. До виведення диференційного рівняння нерозривності потоку.

Тоді через праву грань в ту саму мить часу вийде маса:

Приріст маси в об’ємі паралелепіпеда вздовж вісі _:

Приріст маси в об’ємі паралелепіпеда вздовж осей тазнайдемо по аналогії:

Загальний приріст маси по всьому об’єму дорівнює сумі її приростів вздовж координатних осей:

Разом з тим зміна маси в об’ємі паралелепіпеда можлива тільки внаслідок зміни густини в цьому об’ємі:

Прирівнявши два останні вирази та скоротивши, отримаємо:

Рівняння являє собою диференційне рівняння неперервності потоку для невстановленого руху стискаємої рідини.

Якщо ітоді рівняння спрощується

*

Рівняння (*) являє собою диференційне рівняння неперервності нестискаємої рідини.

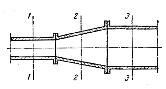Щоб перейти від елементарного об’єму до всього об’єму рідини, який рухається по трубопроводу без пустот і розривів необхідно проінтегрувати вираз *. Якщо переріз трубопроводу постійний, то інтегрування рівняння (*) дало б наступну залежність:

Рис. 3.2. До виведення рівняння нерозривності (суцільності) потоку.

Якщо ж площа перерізу трубопроводу перемінна, то, інтегруючи також по площі, отримаємо:

Для трьох різних перерізів трубопроводу, маємо

**

або

де - масовий видаток рідини,.

Рівняння (**) являє собою рівняння нерозривності (суцільності) потоку в інтегральній формі.

Для крапельних рідин і рівняння набуває вигляду

Отже

або

де - об’ємний видаток рідини,.

Із рівняння видно, що швидкість крапельної рідини в різних перерізах обернено пропорційна площі цих перерізів.

Диференційне рівняння руху рідини. Рівняння Ейлера для ідеальної рідини

Ідеальною називається така рідина, яка має постійну густину, а її динамічна в’язкість рівна нулю.

Розглянемо встановлений рух рідини, яка рухається без тертя. Виділимо в потоці рідини елементарний паралелепіпед об’ємом , де- ребра паралелепіпеда, спрямовані паралельно координатним осям. Проекції сил, які діють на виділений паралелепіпед, складають:

для вісі _:

для вісі _:

для вісі _:

Згідно основного принципу динаміки сума проекцій сил, які діють на елементарний об’єм рідини що рухається дорівнює добутку маси рідини на прискорення.

Якщо рідина рухається зі швидкістю , то прискорення дорівнює. Для координатних осей прискорення буде відповідно. Згідно основного принципу динаміки

або після спрощення

*

В рівняннях системи - субстанційна (повна) похідна. Для координатних осей

**

Система (*) з урахуванням рівнянь (**) являє собою диференційні рівняння руху ідеальної рідини Ейлера для встановленого потоку.