Аналіз системи рівнянь

Із перших двох рівнянь видно, що по вісі і по вісі тиск не змінюється, а змінюється тільки по висоті.

Вивід основного рівняння гідростатики

Для отримання закону розподілу тиску по всьому об’ємі необхідно проінтегрувати систему диференційних рівнянь. В зв’язку з тим що в цій системі частинні похідні ірівні нулю, то тоді частинна похідна в третьому рівнянніможе бути замінена на повну. Приймаючи, що густина і прискорення вільного падіння величини постійні, маємо:

Звідки після інтегрування отримаємо:

де - геометричний напір, висота розташування точки над площиною порівняння,- гідростатичний напір

Для двох горизонтальних площин 1 та 2 рівняння (1.4) виражають у вигляді:

(*)

Рівняння (*) являє собою основне рівняння гідростатики.

Із рівняння виходить, що сума геометричного і гідростатичного напорів є величина постійна для кожної точки рідини в стані спокою.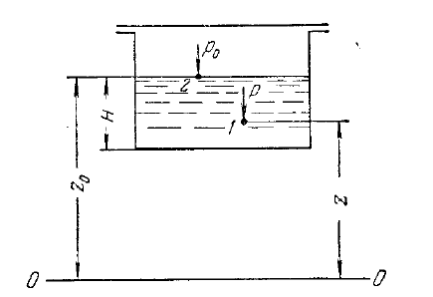

Основне рівняння гідростатики – це один із випадків закону збереження енергії, який можна сформулювати так: сума питомих енергій положення і тиску є величина постійна або питома потенціальна енергія для всіх точок рідини, що знаходиться в стані спокою, є величина постійна.

Рис. 2.2. До основного рівняння гідростатики.

Рівняння (2.5) можна записати у вигляді

або

Рівняння являється виразом закону Паскаля, згідно з яким тиск, що створюється в любій точці нестискаємої рідини що знаходиться в стані спокою, передається однаково всім точкам її об’єму.

Випадки практичного використання основного рівняння гідростатики Принцип дії з’єднаних посудин

Нехай дві відкриті з’єднані посудини заповнені рідиною густиною . Оберемо довільну площину порівняння0–0 і деяку точку А, таку що знаходиться всередині рідини і належить цій площині. Якщо вважати, що точка А належить лівій посудині, то тиск в даній точці згідно закону Паскаля буде: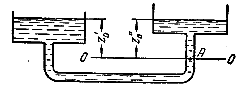

Рис. 2.3.Умова рівноваги в сполучених посудинах з однорідною рідиною.

Якщо ж вважати точку А такою, що належить лівій посудині, то тиск в ній буде:

(, так як площина0–0 проходить через точку А)

У стані рівноваги для кожної точки тиск однаковий в будь-якому напрямку (в іншому випадку мав би місце рух рідини).

Отже

або

Аналогічний висновок міг би бути зроблений для двох закритих з’єднаних посудин, в яких тиск над вільною рідиною однаковий.

Таким чином, в відкритих або закритих з’єднаних посудинах, які знаходяться під однаковим тиском, заповнені однорідною рідиною, її рівні розташовуються на однаковій висоті незалежно від форми і поперечного перерізу посудин. Цей принцип використовується для вимірювання рівня рідини в закритій посудині за допомогою мірних шибок.

Якщо з’єднані посудини заповнені двома рідинами, що не змішуються і мають густини (ліва посудина) і(права посудина), то при проведенні площини порівняння0–0 через границю поділу між рідинами, аналогічно попередньому одержимо: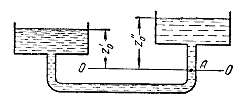

Рис. 2.3.Умова рівноваги в сполучених посудинах з неоднорідними рідинами.

або

звідси випливає, що в з’єднаних посудинах висота рівня різнорідних рідин над поверхнею їх розділу обернено пропорційна густинам цих рідин.

Якщо посудини заповнені однією рідиною з густиною , але тиск над рівнем рідини в них неоднаковий і дорівнює(ліва посудина) і(права посудина), тоді:

Звідси різниця рівнів в посудинах може бути визначена із співвідношення:

Ця властивість використовується в диференційних U-подібних манометрах.