Закон теплопровідності (закон Фур’є)

Закон був написаний у 1822 році.

Кількість теплоти , що проходить шляхом теплопровідності через елемент ізотермічної поверхніза час, прямо пропорційний градієнту температур, величині ізотермічної поверхні і часу. Знак мінус показує, що теплота передається в напрямку протилежному градієнту температур. Теплова енергія вимірюється в Джоулях.

Величину, яка характеризує кількість теплової енергії за одиницю часу називають тепловим потоком

Величину, яка характеризує кількість теплової енергії за одиницю часу на одиницю площі називають густиною теплового потоку.

де - коефіцієнт теплопровідності, показує, яка кількість теплоти проводиться шляхом теплопровідності в одиницю часу через одиницю площі поверхні при різниці температур в один градус на відстань одного метра.

Коефіцієнт - визначається експериментально і знаходиться по довідниках. Цей коефіцієнт залежить від роду матеріалу (твердого тіла) і температури. Для одних тіл коефіцієнт теплопровідності збільшується зі збільшенням температури, для інших зменшується.

Диференціальне рівняння теплопровідності

Для виведення рівняння теплопровідності будуть зроблені наступні припущення:

1. тіло приймається однорідним та ізотропним;

2. всі фізичні параметри тіла (густина, теплоємність, теплопровідність) – постійні;

3. в тілі відсутні джерела і стоки тепла;

4. нехтується теплова деформація.

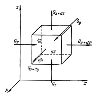
Виділимо в тілі довільної форми елементарний паралелепіпед об’ємом, де- ребра елементарного паралелепіпеда, паралельні координатним вісямівідповідно. Припустимо, що тепло переноситься шляхом теплопровідності, тобто через паралелепіпед проходить певна кількість теплоти. Тоді кількість теплоти, що входить в паралелепіпед через ліву грань:

де - густина теплового потоку через ліву грань площею.

Кількість теплоти, яка виходить через праву грань може бути розкладена в ряд Тейлора:

Приймаючи до уваги перші два члени, нехтуючи рештою через їх малу величину, маємо

Рис.6.3. До виводу ди-ференційного рівняння теплопровідності.

Різниця між кількістю теплоти, що вийшла і ввійшла

По аналогії можемо записати

для вісі

для вісі

Приймаючи

підставивши це в попереднє отримаємо:

З іншого боку, згідно з законом збереження енергії, приріст теплоти в паралелепіпеді рівний зміні ентальпії паралелепіпеда при постійному тиску.

Якщо прирівняти два останні вирази, то будемо мати:

Приймемо, що

після відповідних скорочень отримаємо:

Останнє рівняння є диференціальним рівнянням теплопровідності для нерухомого тіла. Тут - коефіцієнт температуропровідності, який характеризує теплопровідні властивості тіла,. Чим більшим буде значення- тим швидше поширюється тепло і навпаки, чим меншим буде значення цього коефіцієнта тим повільніше поширюється тепло.

Якщо про інтегрувати рівняння теплопровідності то отримаємо функцію температурного поля

тобто диференціальним рівнянням теплопровідності є записом функції температурного поля в диференціальній формі.

Для стаціонарних процесів, коли можемо записати

але , тоді

рівняння стаціонарного температурного поля.

Коли температурне поле стаціонарне і однорідне , то

диференціальне рівняння теплопровідності для одномірного стаціонарного температурного поля.