Тесты по теории автоматического регулирования (ТАР). Кафедра “Системы автоматического управления” / ТАР тесты косвенные оценки(7)

Переходные процессы и косвенные оценки.

№1

Что определяют с помощью построенного процесса регулирования (убрать неправильный ответ):

1. Время регулирования

2. Колебательность системы.

3. Вид процесса (апериодический, колебательный).

4. Перерегулирование.

№2

Дифференциальное уравнение системы имеет вид: . При каком входном сигнале в момент координата и ее производная не будут иметь разрывы первого рода:

1. 3.

2. 4. .

№3

В момент времени левые и правые начальные условия по управляемой переменной и ее производным не совпадают. Возможно ли в этом случае аналитическое решение дифференциального уравнения САУ и, если да, то как:

1. Решение невозможно.

2. Да, при этом в изображениях по Лапласу производных функций должны учитываться левые начальные условия.

3. Да, при этом в изображениях по Лапласу производных функций должны учитываться левые начальные условия по и правые по .

4. Да, при этом в изображениях по Лапласу производных функций должны учитываться правые начальные условия по и левые по .

№4

Дифференциальное уравнение системы имеет вид: . При каком входном сигнале в момент координата или ее производная будут иметь разрывы первого рода:

1. 3.

2. 4. .

№5

При частотном методе построения переходного процесса управляемая переменная определяется зависимостью . В числителе подынтегрального выражения на пустом месте находится:

1. Вещественная частотная характеристика замкнутой системы.

2. Вещественная частотная характеристика разомкнутой системы.

3. Мнимая частотная характеристика замкнутой системы.

4. Мнимая частотная характеристика разомкнутой системы.

№6

При частотном методе построения переходного процесса управляемая переменная определяется зависимостью . В числителе подынтегрального выражения на пустом месте находится:

1. Вещественная частотная характеристика замкнутой системы.

2. Вещественная частотная характеристика разомкнутой системы.

3. Мнимая частотная характеристика замкнутой системы.

4. Мнимая частотная характеристика разомкнутой системы.

№7

Дифференциальное уравнение САУ имеет вид . Входной сигнал . В какие моменты времени возникают скачки по управляемой переменной или ее производной:

1. При 3. При

2. При и 4. При .

№8

Дифференциальное уравнение САУ имеет вид . Входной сигнал . В некоторые моменты времени возникают скачки по управляемой переменной или ее производной. Для выполнения численного расчета переходного процесса данное уравнение должно быть приведено к виду:

1. 3.

2. 4. .

№9

Дифференциальное уравнение САУ имеет вид . Входной сигнал . В некоторые моменты времени возникают скачки по управляемой переменной или ее производной. Для выполнения численного расчета переходного процесса данное уравнение должно быть приведено к виду:

1. 3.

2. 4. .

№10

АФЧХ замкнутой системы . Установившееся значение переходной характеристики равно:

1. 3.

2. 4. .

№11

АФЧХ замкнутой системы . Достаточным условием того, что перерегулирование % не превышает 18%, является выполнение условия:

1. может быть представлена как разность 3 положительных не возрастающих функций частоты.

2. - положительная не возрастающая функция частоты.

3. - положительная не возрастающая функция частоты.

4. может быть представлена как разность 2 положительных не возрастающих функций частоты.

№12

Если ВЧХ замкнутой САУ является положительной не возрастающей функцией частоты, то:

1. Переходная характеристика является монотонно возрастающей функцией.

2. Импульсная переходная функция является монотонно возрастающей функцией.

3. В переходном процессе перерегулирование не превышает 18%.

4. Процесс регулирования будет заведомо немонотонной функцией времени.

№13

Для того, чтобы переходный процесс был монотонным достаточно, чтобы:

1. Вещественная частотная характеристика являлась положительной не возрастающей функцией.

2. Производная была отрицательной, убывающей по модулю функцией и .

3. Производная была положительной, убывающей по модулю функцией и .

4. Вещественная частотная характеристика может быть представлена как разность 2 положительных не возрастающих функций частоты.

№14

Если вещественная частотная характеристика (, - максимальное значение ВЧХ) может быть представлена как разность 2 положительных не возрастающих функций частоты, то:

1. Переходная характеристика является монотонно возрастающей функцией.

2. В переходном процессе перерегулирование не превышает 18%.

3. Перерегулирование не превышает .

4. Процесс регулирования будет заведомо немонотонной функцией времени.

№15

Степень устойчивости это:

1. Модуль вещественной части корня, ближайшего к вещественной оси.

2. Модуль вещественной части корня, ближайшего к мнимой оси.

3. Модуль мнимой части корня, ближайшего к мнимой оси.

4. Модуль мнимой части корня, ближайшего к вещественной оси.

№16

Характеристическое уравнение системы имеет следующие корни: . Степень устойчивости равна:

1. -2 2. 0,6 3. 6 4. 1/2.

№17

Характеристическое уравнение системы имеет следующие корни: . Степень устойчивости равна:

1. 1 2. 2,5 3. 1,2 4. -1.

№18

Пусть - величина «коридора», определяющего окрестность установившегося значения управляемой величины, по которой находится время регулирования , - степень устойчивости. Приближенная оценка времени регулирования имеет вид:

1. 3.

2. 4. .

№19

Пусть - величина «коридора», определяющего окрестность установившегося значения управляемой величины, по которой находится время регулирования , - степень устойчивости. При приближенная оценка времени регулирования имеет вид:

1. 3.

2. 4. .

№20

Номограмма Солодовникова определяет:

1. Зависимость перерегулирования и времени регулирования от максимального значения ВЧХ .

2. Зависимость установившейся ошибки от максимального значения ВЧХ .

3. Зависимость избытка по амплитуде и избытка по фазе от максимального значения ВЧХ .

4. Зависимость избытка по амплитуде и избытка по фазе от минимального значения ВЧХ .

№21

Характеристическое уравнение системы третьего порядка имеет следующие корни: . Колебательность системы определяется выражением:

1. 3.

2. 4. .

№22

С увеличением колебательности :

1. Колебания в системе затухают сильнее.

2. Затухание колебаний не зависит от этого параметра.

3. Апериодическая составляющая процесса регулирования затухает сильнее.

4. Колебания в системе затухают слабее.

№23

В системе заданы ограничения на степень устойчивости , так что выполняется условие и колебательность , так что выполняется условие . При этом область возможного расположения корней характеристического уравнения на комплексной плоскости «р» имеет вид:

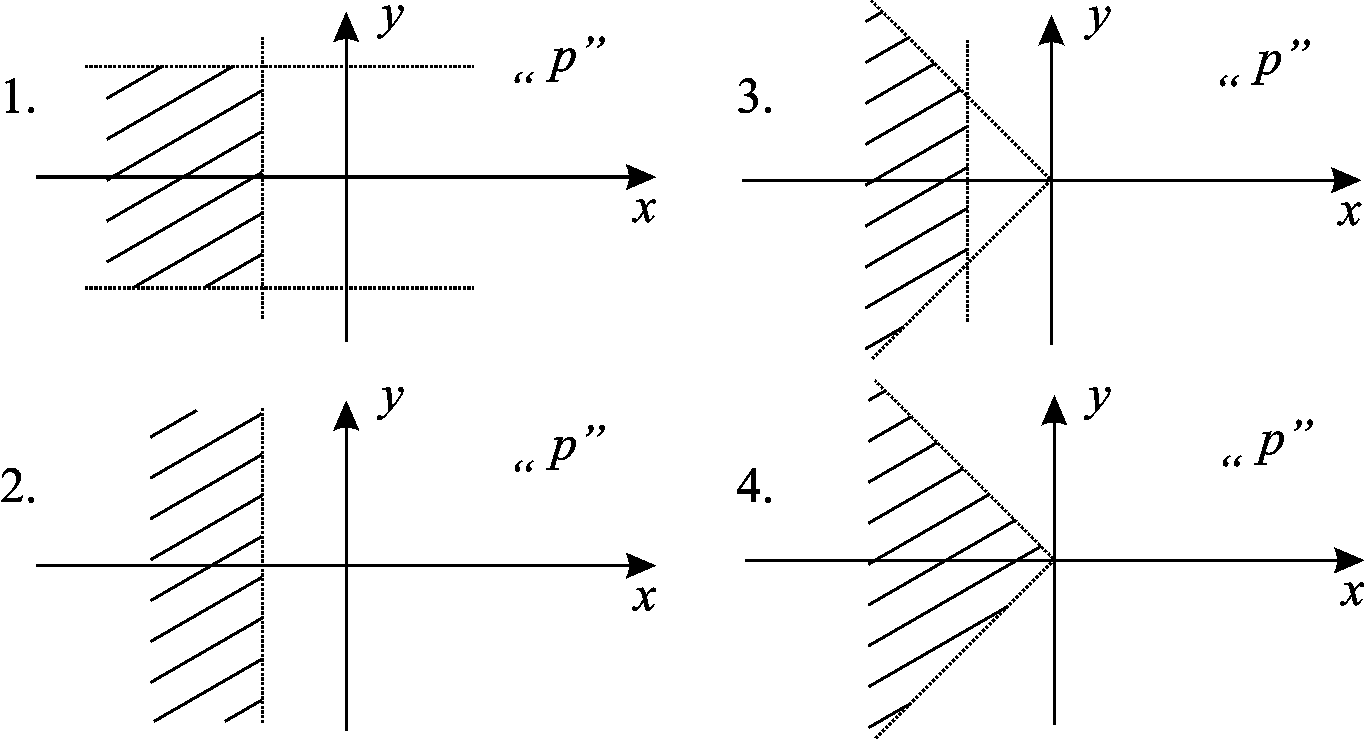4

№24

В системе заданы ограничения на степень устойчивости , так что выполняется условие . При этом область возможного расположения корней характеристического уравнения на комплексной плоскости «р» имеет вид:

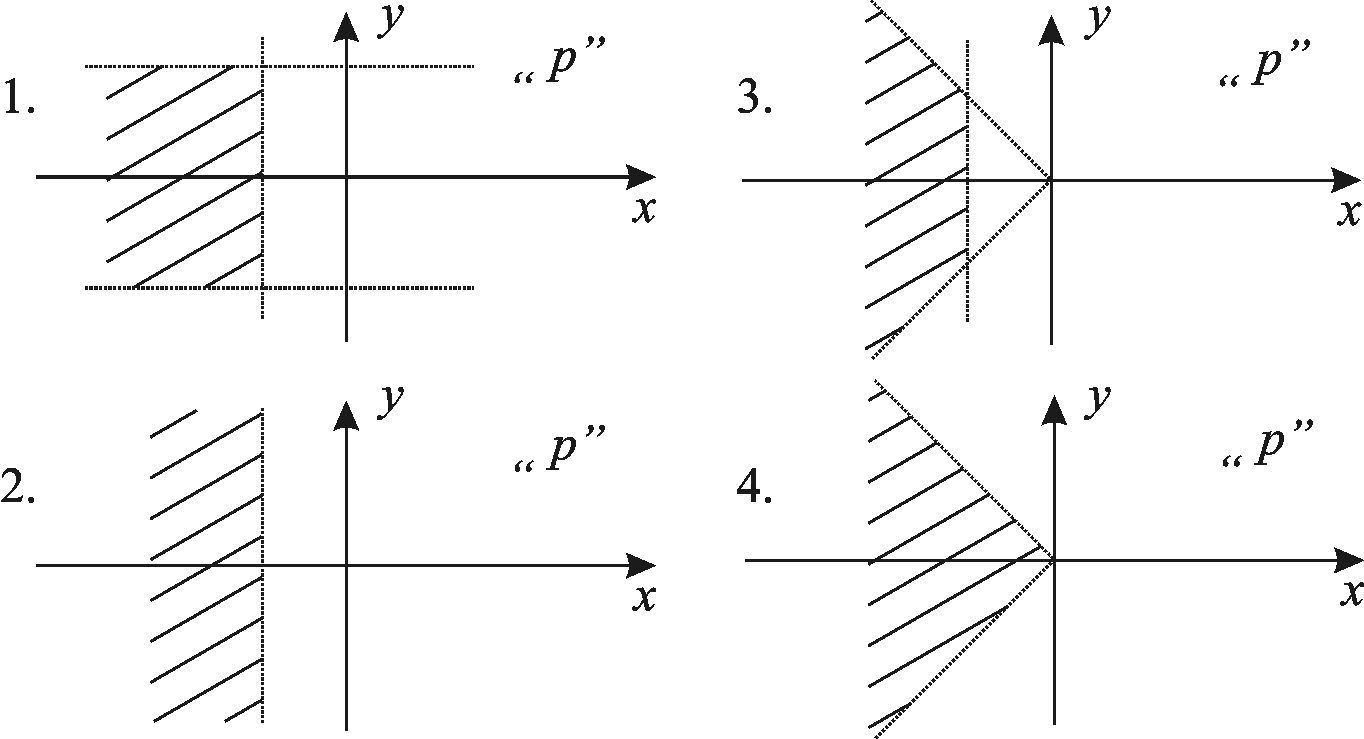2

№25

В системе заданы ограничения на колебательность , так что выполняется условие .При этом область возможного расположения корней характеристического уравнения на комплексной плоскости «р» имеет вид:

4

№26

Характеристическое уравнение системы имеет следующие корни: . Колебательность системы равна:

1. 2 2. 16 3. 8 4. 4.

№27

Характеристическое уравнение системы имеет следующие корни: . Колебательность системы равна:

1. 21 2. 7/3 3. 3/7 4. 7.

№28

При выборе нулей и полюсов передаточной функции системы желательно:

1. Удалять нули передаточной функции от полюсов.

2. Относительное расстояние нулей и полюсов не влияет на переходные процессы в системе.

3. Сближать нули и полюсы передаточной функции.

4. Удалять нули друг от друга.