3. Метод предельных состояний, схематичная структура метода.

Расчёт по деформативности изгибаемых железобетонных элементов.

Метод расчета прочности сечений изгибаемых эле­ментов по допускаемым напряжениям исторически сфор­мировался первым; в нем за основу взята стадия II на­пряженно-деформированного состояния и приняты сле­дующие допущения: бетон растянутой зоны не работает, растягивающее напряжение воспринимается арматурой; бетон сжатой зоны работает упруго, а зависимость меж­ду напряжениями и деформациями — линейная согласно закону Гука; нормальные к продольной оси сечения, пло­ские до изгиба, остаются плоскими после изгиба (гипо­теза плоских сечении).

Как следствие этих допущений, в бетоне сжатой зоны принимаются треугольная эпюра напряжений и постоянное отношение модулей упругости материалов а = Е3/Еь (рис, 1.2.3.). Рассматривают приведенное однородное, се­чение, в котором площадь сечения растянутой арматуры As заменяют площадью сечения бетона, равной aAs, а площадь сечения сжатой арматуры A's —площадью сечения бетона aA's. Исходя из равенства деформаций бетона и арматуры.

а также используя отношение а устанавливают зависи­мость между напряжениями в арматуре и бетоне.

где: - отношение модуля упругости арматуры и бетона.

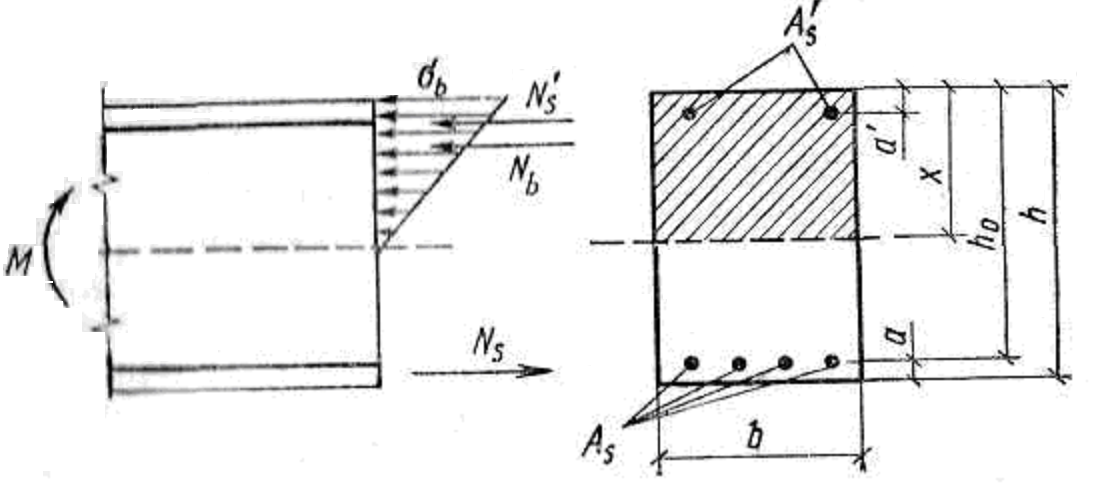
Рис. 1.2.3.К расчету балки прямоугольного сечения по допускаемым напряжениям.

Краевое напряжение в бетоне определяют как для приведенного однородного сечения

г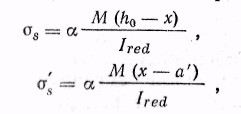де х — высота сжатой зоны. Напряжения и растянутой и сжатой арматуре,Ired- момент инерции приведенного сечения. М- внешний силовой фактор.

где h0— рабочая (полезная) высота сечения; h — полная вы­сота сечения; а — расстояние от оси, нормальной к плоскости изгиба и проходящей через центр тяжести сечения растянутой арматуры, до внешнего растянутого края сечения, а'— расстояние от оси, нор­мальной к плоскости изгиба и проходящей через центр тяжести се­чений сжатой арматуры, до внешнего сжатого края сечения.

Высоту сжатой зоны сечения χ находят из условия, что статический момент приведенного сечения относи­тельно нейтральной оси равен нулю

(2.6)

Момент инерции приведенного сечения

(2.7)

Напряжения в бетоне и арматуре ограничивают до­пускаемыми напряжениями, которые устанавливают как некоторые доли временного сопротивления бетона сжатию(где R — марка бетона, принимаемая равной кубиковой прочности бетона) и предела текуче­сти арматуры

Основной недостаток метода расчета сечений по до­пускаемым напряжениям заключается в том, что бетон рассматривается как упругий материал.

4. Метод предельных состояний, схематичная структура метода.

Расчёт по трещиностойкости изгибаемых железобетонных элементов.

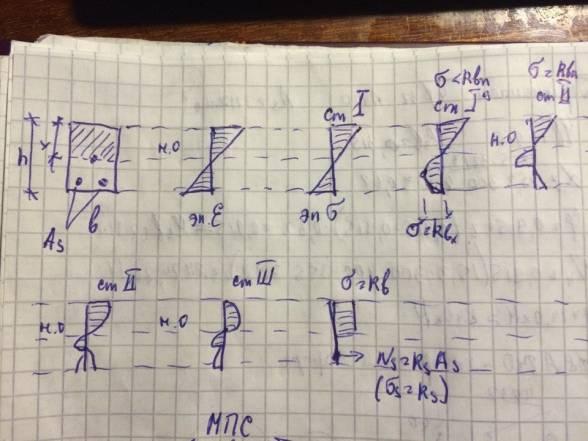
Метод предельных состояний:

Прочность (ст.III) – I группа ПС; 2. Жесткости (ст.I, Ia, II); 3- Трещиностойкости: (по образованию трещин (ст Ia) – I группа ПС и по ширине раскрытия (ст II)

Расчет железобетонных элементов по образованию нормальных трещин производится из условия: М_r < М_crc,

где М_r – момент внешних сил, расположенных по одну сторону от рассматриваемого сечения, относительно оси, параллельной нулевой линии и проходящей через ядровую точку, наиболее удаленную от растянутой зоны, трещинообразование которой проверяется;

М_crc – момент, воспринимаемый сечением, нормальным к продольной оси элемента при образовании трещин, и определяемый по формуле

Расчет по раскрытию трещин производят из условия:

где а_crc – ширина раскрытия трещин от действия внешней нагрузки,

a_crc,ult – предельно допустимая ширина раскрытия трещин.

Момент образования трещин в стадии эксплуатации определяют по формуле

где – момент сопротивления, приведенного сечения для крайнего растянутого волокна

Ш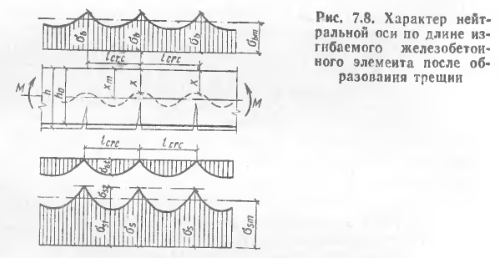ирина раскрытия нормальных трещин определяется по формуле

где– приращение напряжений в в сечении с трещиной, от внешней нагрузки;

–базовое (без учета вида внешней поверхности арматуры) расстояние между смежными трещинами;

–коэффициент, учитывающий продолжительность действия нагрузки, принимаемый равным:

–коэффициент, учитывающий профиль арматуры и принимаемый равным:

–коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами. Допускается принимать; если при этом условие (3.1) не выполняется, тоопределяют по формуле:где– приращение напряжений в растянутой арматуре в сечении с трещиной сразу после образования трещин, определяемое по тем же формулам, что и , но при М = М_crc;

–то же, при действии рассматриваемой нагрузки.