21. Деформативные свойства каменной кладки. Начальный модуль упругости и модули деформаций кладки. Упругая характеристика кладки.

В каменной кладке различают следующие деформации:

- объемные, возникающие во всех направлениях, вследствие усадки раствора и камня

или от изменения температуры;

- силовые, развивающиеся, главным образом, вдоль направления действия силы.

Усадочные деформации кладки εst, зависят от материала кладки.

Температурные деформации кладки также зависят от материала кладки и коэффициента

линейного расширения кладки – αt.

При действии нагрузки (силовые деформации) каменная кладка представляет собой упругопластический материал, и поэтому при действии нагрузки зависимость между напряжениями и деформациями не подчиняется закону Гука. Начиная с небольших напряжений в кладке, кроме упругих, развиваются и пластические деформации. Поэтому

силовые деформации будут зависеть от характера приложения нагрузки и могут быть трех видов:

- деформации при однократном загружении кратковременной нагрузкой;

- деформации при длительном действии нагрузки;

- деформации при многократно повторных нагрузках.

Е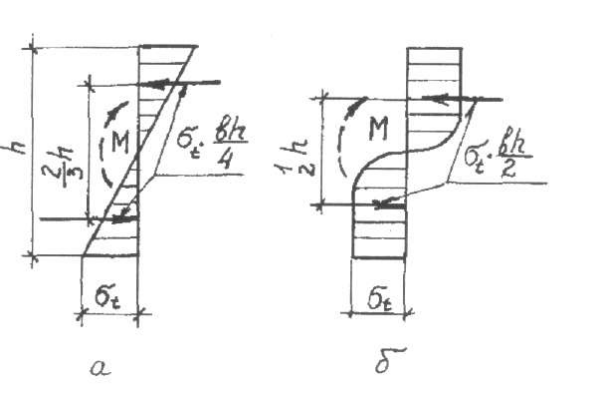сли каменную кладку нагружать очень быстро и довести до разрушения за несколько секунд, то в кладке возникнут только упругие деформации и кладка будет работать как упругий материал, а зависимость между напряжениями и деформациями будет линейной. Если каменную кладку в лабораторных условиях загружать в течение одного часа постепенно до разрушения, то зависимость между напряжениями и деформациями получается нелинейной; для данного случая кривая зависимости σ - ε показана на рис. 10.14. Таким образом, полные деформации будут слагаться из упругих и неупругих. В этом случае модуль деформации кладки- Е будет величиной временной: d dtg

С возрастанием напряжения угол φ уменьшается и, следовательно, уменьшается и модуль деформаций.

Наибольшее значение модуль деформаций будет иметь при φ = φ0, то есть E0=tgφ0 - это начальный или мгновенный модуль упругости, величина которого для данного вида кладки является постоянной. Экспериментально установлено, что начальный модуль деформаций E0 (модуль упругости кладки) пропорционален временному сопротивлению сжатию кладки - Ru.

22. Расчет по несущей способности центрально сжатых элементов каменных конструкций.

Расчет элементов неармированных каменных конструкций при центральном сжатии производится по формуле

,

где N - расчетная продольная сила; R - расчетное сопротивление сжатию кладки; φ - коэффициент продольного изгиба;

A - площадь сечения элемента; m_q – коэффициент, учитывающий длительность действия нагрузки.

Р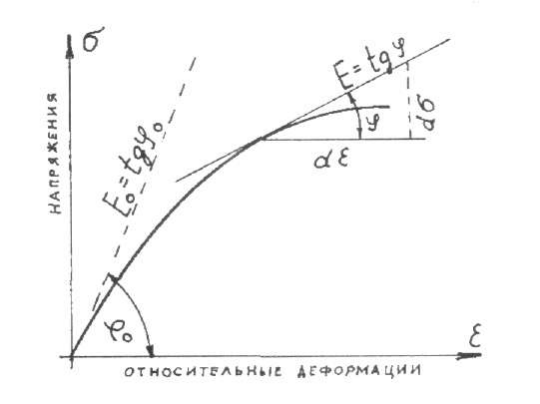асчет (подбор сечения) центрально сжатого элемента (столба) по формуле (4.1) осуществляется методом последовательного приближения и заключается в следующем:

а) определяются нагрузки для рассчитываемого столба N и N_g (на уровне того или иного этажа), вычисляя их как сумму нагрузок от всех этажей, лежащих выше расчетного сечения столба с приближенным учетом собственной массы столба как нагрузки, составляющей 5…10% от расчетной;

б) выбирается материал кладки (вид и марка камней и вид и марка раствора) и оценивается ее расчетное сопротивление R;

в) задается некоторое значение φ, по которому принимаются соответствующие значения λ_h (λ_i);

г) по найденной гибкости λ_h (λ_i) определяется коэффициент η;

д) используя предварительно собранные на столб нагрузки N и N_g, определяется коэффициент m_g;

е) по формуле (4.1) вычисляется площадь поперечного сечения столба А

,

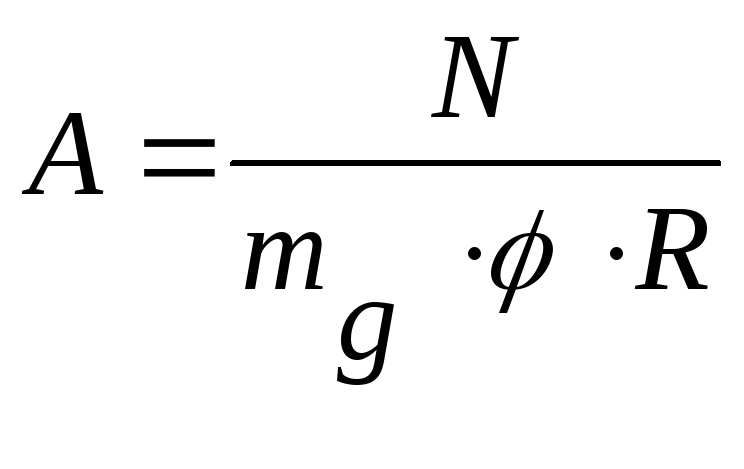отвечающая при заданной нагрузке материалу кладки и принятому коэффициенту φ;

ж) значение А из формулы (4.2) выражаем через конкретные размеры поперечного сечения столба h x b = A, если столб прямоугольный, или h x h = A, если столб квадратный, округляя их до величин, кратных (с учетом толщины швов кладки) размерам кирпича (камня) в плане;

з) по принятым геометрическим размерам поперечного сечения столба, упругой характеристике кладке α и расчетной высоте столба вычисляется его гибкость λ_h (λ_i);

и) находим коэффициенты φ и η, соответствующие λ_h (λ_i) по п. з) и определяем коэффициент m_q;

к) полученные значения φ и m_g, точнее произведение этих коэффициентов φ·m_g, сравниваем с исходным. Если полученное произведение (φ·m_g)_пол отличается от исходного (φ·m_g)_исх более чем на 5%, т.е. имеет место неравенство

,

то расчет следует повторить, приняв полученные значения φ и m_g за исходные.

Расчет считается законченным при удовлетворении неравенства

.

Окончательные размеры поперечного сечения столба соответствуют последнему значению (φ·m_g)_исх в изложенном процессе последовательного приближения.

Процесс последовательного приближения удобнее начинать с φ=1,0. В этом случае η=0 и m_{g исх}=1,0. Следует также учитывать условие m_g=1,0, если h≥30 см или i≥8,7 см.

Расчеты показывают, что, как правило, достаточно 1-2 приближений для удовлетворения неравенства (4.4).