3. Кореляційно-регресійний метод

(ПАРНІ ЗВ’ЯЗКИ)

Метод кореляційно-регресійного аналізу (КРА) застосовується, коли ознака, вплив якої вивчається, кількісна, а зв’язки кореляційні⁶⁷. Проведення КРА при побудові парних зв’язків передбачає вирішення низки проблем.

Перш за все шляхом якісного аналізу показників, що досліджуються, визначається коло показників-чинників, які, на думку дослідника, більш за все можуть впливати на результативну ознаку. Після цього слід перейти до вибору форми зв’язку між результативною ознакою та відібраними чинниками (при парних зв’язках – одним найбільш суттєвим чинником).

Вибір форми зв’язку здійснюється у залежності від способу розрахунків і обсягу сукупності, що вивчається. Якщо обчислення ведуться на комп’ютері, то розраховуються показники тісноти зв’язку⁶⁸ при різних його формах (прямій, параболі, гіперболі тощо) і відбирається та форма, при якій коефіцієнт взаємозв’язку буде найбільшим.

Коли ж обчислення проводяться без комп’ютера, а обсяг сукупності не перевищує 30 одиниць (мала вибірка), то для виявлення наявності, напряму і форми зв’язку між двома ознаками, із яких одна є факторною, а друга – результативною, застосовується кореляційне поле. Воно являє собою точковий графік (діаграму розсіювання), побудований у прямокутній системі координат, де на осі абсцис відкладаються значення факторної ознаки “”, а на осі ординат – відповідні значення результативної ознаки “”. Кожній одиниці сукупності на графіку відповідає окрема точка з абсцисою і ординатою , а всі одиниці сукупності утворюють скупчення точок, яке й називають кореляційним полем. За характером розміщення точок на ньому візуально визначаються те тільки наявність і напрям зв’язку, а й його аналітична форма.

Зовнішній вигляд кореляційного поля наведено на рис. 7.3 за даними табл. 7.3. З візуального аналізу отриманого кореляційного поля можна дійти висновку про наявність прямої та достатньо сильної залежності між ознаками, що розглядаються.

у

9

7

5

3

1

х

1 2 3 4 5 6 7

Рис. 7.3. Кореляційне поле.

При обсязі сукупності понад 30 одиниць вона групується звичайним способом за факторною ознакою і за результатами цього групування будується емпірична лінія регресії. Це ламана лінія, що поєднує середні значення ““ у кожному інтервалі “” . За характером емпіричної лінії регресії також візуально робиться припущення про форму зв’язку.

Для встановлення наявності та спрямованості зв’язку достатнього поширення набували кореляційні таблиці, які викладають матеріал стисло, компактно. В них факторна ознака “” розташовується звичайно у рядках, а результативна ознака ““ – у стовпчиках таблиці. Числа, що знаходяться у таблиці на перетині рядків і стовпчиків, показують частоту повторення даного сполучення значень “” і “”.

Побудова кореляційної таблиці починається з групування одиниць спостереження за значеннями факторної та результативної ознак. Якщо частоти у кореляційній таблиці розташовані за діагоналлю з лівого верхнього кутка у правий нижній (тобто більшим значенням аргументу відповідає більше значення функції), то можна припустити наявність прямої кореляційної залежності. Коли ж частоти розташовані за діагоналлю справа наліво, то припускають наявність оберненого зв’язку між досліджуваними ознаками.

Доречно підкреслити, що при розгляданні кореляційної таблиці важливо встановити розміщення основної маси частот. Можливі варіанти, коли усі клітинки кореляційної таблиці виявляться заповненими. Але це ще не означає відсутності кореляційного зв’язку між ознаками. Слід установити, як розташована у таблиці основна маса одиниць.

Таким чином, кореляційна таблиця навіть при загальному знайомстві дає можливість установити наявність або відсутність зв’язку і з’ясувати його спрямованість (табл. 7.4).

У подальшому аналізі слід вести розрахунки параметрів рівняння регресії, що характеризує зміну середнього рівня результативної ознаки “” залежно від зміни факторної ознаки “”. Для моделювання залежностей між ознаками можуть бути застосовані різні елементарні функції – пряма, парабола, гіпербола, логістична, степенна та ін. Найпростішою з них за розрахунком та інтерпретацією результатів є лінійна функція (рівняння прямої). Її доречно застосовувати, коли середні значення результативної ознаки змінюються (зростають або зменшуються) рівномірно зі зміною значень факторної ознаки. В інших випадках підбирається одна з криволінійних функцій.

Визначення параметрів рівняння регресії у практиці економіко-статистичного аналізу залежностей частіше за все ведеться за методом найменших квадратів, згідно з яким сума квадратів відхилень фактичних значень результативної ознаки () від значень, що знайдено за рівнянням регресії (), повинна бути найменшою:

. (48)

Іншими словами, цей метод дає змогу обчислити такі параметри рівняння регресії, за якими теоретична лінія регресії найбільш наблизиться до точок лінії, побудованої за фактичними даними.

У разі вивчення залежності результативної ознаки лише від однієї факторної (при парних зв’язках) рівняння регресії можна записати у вигляді рівняння прямої:

, (49)

де - розрахункове значення результативної ознаки;

- факторна ознака;

- параметр рівняння, вільний член;

- параметр рівняння, коефіцієнт регресії.

Щоб визначити параметри цього рівняння за методом найменших квадратів, слід розв’язати систему двох рівнянь з двома невідомими:

(50)

Розв’язання наведеної системи рівнянь, тобто проведення усіх проміжних перетворень, дає змогу дістати такі формули для обчислення параметрів лінійного рівняння регресії:

; (51)

, (52)

де - середня з добутків значень обох ознак ();

- середня факторної ознаки ();

- середня результативної ознаки ();

- дисперсія факторної ознаки ().

Параметр рівняння дає значення “” при = 0. Але якщо не може дорівнювати нулю, то в економічному смислі не інтерпретується і як вільний член рівняння регресії має тільки розрахункове значення.

Коефіцієнт регресії у лінійному рівнянні має економічне тлумачення і показує, на скільки одиниць власного виміру зміниться середнє значення результативної ознаки “” внаслідок зміни факторної ознаки “” на одну одиницю її власного вимірювання. А знак коефіцієнта (плюс або мінус) вказуватиме на напрямок цієї залежності (прямий або зворотний).

Слід зауважити, що у статистичному аналізі є показник, який характеризує аналогічні залежності між ознаками, але тільки не в абсолютному вимірі, а у відносних величинах. Цей показник називається коефіцієнтом еластичності () і показує, на скільки відсотків зміниться результативна ознака внаслідок зміни факторної на 1%. Напрямок залежності при цьому також визначається знаком, з яким отримано результат розрахунку.

Для лінійної функції коефіцієнт еластичності знаходиться так:

. (53)

Таким чином, вирішення ще однієї проблеми проведення КРА, а саме: визначення параметрів рівняння регресії дає змогу перейти до оцінки тісноти зв’язку між ознаками, що досліджуються.

Оцінка тісноти зв’язку при лінійній залежності між ознаками здійснюється через розрахунок лінійного коефіцієнта кореляції – . Він найдосконаліше характеризує тісноту лінійного зв’язку і розраховується за формулами:

(54) або , (54-а)

де , , , - те ж саме;

- середні квадратичні відхилення відповідно для факторної та результативної ознак.

Зазначимо, що за ступенем тісноти зв’язку між досліджуваними ознаками відрізняють слабкі і сильні зв’язки. Ця характеристика дає змогу в конкретній формі визначити ступінь тісноти зв’язку між явищами, що вивчаються. Вона виражається конкретними величинами статистичних показників зв’язку і їх тлумачення здійснюється за загальноприйнятими критеріями тісноти зв’язку для конкретних показників її вимірювання.

Лінійний коефіцієнт кореляції змінюється у межах від –1 до +1. Знак “мінус” вказує на обернений, а знак “плюс” – на прямий зв’язок між ознаками, що аналізуються. Наближення розміру показника до (±1) свідчить про підвищення тісноти зв’язку, а зменшення його до нуля вказує на відсутність зв’язку між факторною та результативною ознаками. Піднесення величини лінійного коефіцієнта кореляції до другого ступеня () дає коефіцієнт детермінації, зміст якого нічим не відрізняється від раніше розглянутого, а саме: він характеризує частку коливання результативної ознаки за рахунок факторної.

Отже, настала черга розгляду шляхів вирішення останньої проблеми проведення КРА – оцінки достовірності результатів.

Оцінка істотності (достовірності) показника тісноти зв’язку та параметрів рівняння регресії виконується через критерій Стьюдента (t-критерій). Для кожного з оцінюваних показників визначається розрахункове значення t-критерію, після чого воно зіставляється з табличним для заданого рівня значущості “α =1 – Р” та відповідного числа ступенів свободи.

Коефіцієнт кореляції та параметри рівняння регресії визнаються значущими, якщо табличні величини не перевищують розрахункові.

Для перевірки істотності коефіцієнта кореляції при невеликому числі спостережень розрахунок t-критерію ведеться за формулою: , (55)

де - лінійний коефіцієнт кореляції;

- коефіцієнт детермінації;

(1-) - коефіцієнт залишкової детермінації;

n - обсяг сукупності;

(n –2) - число ступенів свободи.

Розрахунок t-критерію для параметрів рівняння регресії передбачає попереднє визначення залишкового середнього квадратичного відхилення – :

= (56) як і вище, тут - фактичне, а - розрахункове значення залежної перемінної .

Самі значення t-критерію для параметрів рівняння регресії розраховуються за формулами:

- для параметра : ; (57)

- для коефіцієнта регресії : , (58)

де n - обсяг сукупності;

(n –2) - число ступенів свободи;

- середнє квадратичне відхилення за факторною

ознакою.

Покажемо методику проведення КРА на умовному прикладі.

Припустимо, що йдеться про рівень енергоозброєності праці та середній рівень її продуктивності на десятьох дільницях підприємства (табл.7.3). Проведемо аналіз взаємозв’язку між цими показниками.

Таблиця 7.3

Відомості про енергоозброєність праці та її продуктивність

на дільницях підприємства

№ дільниці	1	2	3	4	5	6	7	8	9	10
Енергоозброєність праці, кВт/ос., – Х	3,0	4,4	5,0	6,5	6,7	3,5	4,5	4,0	6,0	7,0
Середній виробіток на 1-го робітника за місяць, тис.грн./ос.,-У	4,6	6,0	6,2	7,5	8,7	4,7	5,2	4,9	7,8	8,8

Для вирішення проблеми вибору форми зв’язку скористаємося кореляційною таблицею (табл. 7.4). Її побудова починається з групування одиниць спостереження за факторною і результативною ознаками. Обидві ознаки є кількісними та безперервними, тому здійснимо інтервальне групування. Величину інтервалу розрахуємо за формулою Стерджесса (2). Оскільки число груп (знаменник дробу) повинно бути цілим числом, округлимо знаменники до чотирьох:

; .

У табл. 7.4 - частота повторення кожної групи значень факторної ознаки в усій сукупності; - частота повторення значень результативної ознаки в усій сукупності. Середній виробіток для дільниць, що мають рівень енергоозброєності праці , наприклад, від 4 до 5 кВт/ос. (друга група), буде дорівнювати: . Для інших груп розрахунки цього показника проведено аналогічно.

Таблиця 7.4

Кореляційна таблиця

Середина інтервалу “У”	5,125	6,175	7,225	8,275		Середнє значення виробітку для дільниць даної групи, тис.грн./ос.
Групи за продуктив- Групи ністю праці за енерго- озброєністю	4,60 – 5,65	5,65 – 6,70	6,70 – 7,75	7,75 – 8,8
Від 3 до 4	2				2	5,125
Від 4 до 5	2	1			3	5,475
Від 5 до 6		1			1	6,175
Від 6 до 7			1	3	4	8,012
	4	2	1	3	10

Таким чином, зростання середніх значень результативної ознаки (останній стовпчик таблиці) з підвищенням значень факторної ознаки (перший стовпчик таблиці) свідчить про можливу наявність прямої кореляційної залежності рівня середнього виробітку від рівня енергоозброєності праці. Виходячи з цього, опишемо рівнянням прямої залежність між “Х” та “У”. Для визначення параметрів рівняння слід попередньо провести багаточисельні розрахунки. Зведемо усі проміжні обчислення у табл. 7.5

; ;

; ;

;

;

;

.

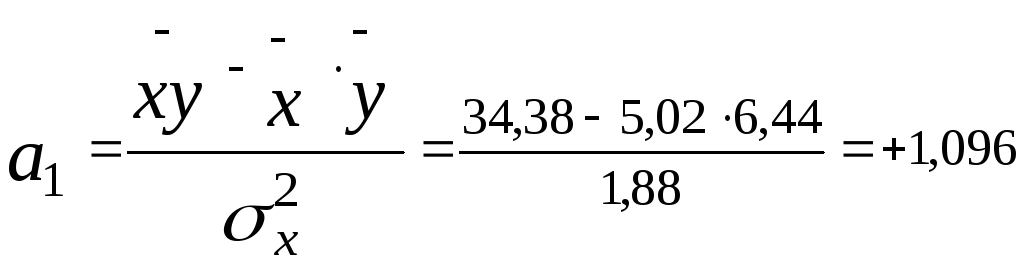Таблиця 7.5

Розрахункова таблиця

№№	1	2	3	4	5	6	7	8	9	10	Разом
	3,0	4,4	5,0	6,5	6,7	3,5	4,5	4,0	6,0	7,0	50,2
	4,6	6,0	6,2	7,5	8,7	4,7	5,2	4,9	7,8	8,8	64,4
	13,8	24,0	31,0	48,8	58,3	16,5	23,4	19,6	46,8	61,6	343,8
	9,0	16,0	25,0	42,3	44,9	12,3	20,3	16,0	36,0	49,0	270,8
	21,2	36,0	38,4	56,3	75,7	22,1	27,1	24,0	60,8	77,4	439,0

Отже, рівняння прямої, що описує взаємозв’язок між ознаками “” і “”, матиме вигляд: .

Виходячи з економічного тлумачення параметрів рівняння, можна сказати, що підвищення енергоозброєності на 1 кВт/ос. призведе до зростання продуктивності праці на 1,096 тис.грн./ос. Одночасно з даного рівняння видно, що при відсутності енергоозброєності, тобто при Х=0, середній виробіток одного робітника за місяць дорівнюватиме 938 грн.

Щоб відбити названу залежність у відсотках, обчислимо коефіцієнт еластичності (форм.53):

.

Цей результат означає, що продуктивність праці зростатиме на 0,85% при підвищенні енергоозброєності на 1%.

Визначимо лінійний коефіцієнт кореляції для встановлення кількісної міри тісноти зв’язку між ознаками, що досліджуються:

, або

.

Отримана величина коефіцієнту (близько +1) свідчить про прямий та значно тісний зв’язок між енергоозброєністю праці та її продуктивністю. Підтвердження або спростування цього висновку можна дістати через оцінку істотності показника тісноти зв’язку та параметрів рівняння регресії за допомогою t-критерію Стьюдента (формули 55,57,58)

Для коефіцієнта кореляції маємо:

.

У таблиці критичних значень t-критерію для рівня значущості “α = 0,05”, тобто з імовірністю 0,95, для восьми ступенів свободи беремо табличне значення і воно дорівнює 2,31, що значно менше, ніж розраховане. А це означає, що отриманий коефіцієнт кореляції визначається значущим, тобто досить точно та з повною гарантією характеризує тісноту зв’язку між енергоозброєністю праці та її продуктивністю.

Як відомо, розрахунок t-критерію для параметрів рівняння регресії потребує знання залишкового середнього квадратичного відхилення (формула 56). Для його обчислення усі проміжні розрахунки також зведемо у табл. 7.6

Таблиця 7.6

Допоміжна таблиця розрахунку залишкового

середнього квадратичного відхилення

№№	1	2	3	4	5	6	7	8	9	10	Разом
	4,6	6,0	6,2	7,5	8,7	4,7	5,2	4,9	7,8	8,8	-
*	4,2	4 ,8	5,3	5,8	5,9	6,4	7,5	8,1	8,5	8,6	-
	+0,4	-0,1	-2,2	+0,2	-0,7	-0,2	+0,3	-0,6	+0,2	+0,2	-
()	0,16	0,01	4,84	0,04	0,49	0,04	0,09	0,36	0,04	0,04	6,11

* Обчислено за рівнянням регресії через підстановку в нього відповідних значень “Х”.

Тепер маємо: =.

Критерій Стьюдента для параметрів рівняння регресії буде становити:

- для параметра : ;

- для параметра : .

Табличне значення t-критерію візьмемо для того ж рівня значущості “α = 0,05” та також для восьми ступенів свободи, тобто знову . Як бачимо, розрахункові значення t-критерію вищі за табличне, а з цього виходить, що параметри отриманого рівняння регресії значущі. Через це рівняння можна описувати з достатньою точністю і повнотою залежність середнього виробітку на 1-го робітника за місяць від енергоозброєності праці.

Отже, розглянуто прийоми вивчення взаємозв’язків між кількісними ознаками або між атрибутивною факторною та кількісною результативною ознаками. Але економічні дослідження досить часто стикаються з необхідністю вивчення кореляційної залежності між ознаками, кожна з яких є атрибутивною. У таких випадках стають у пригоді непараметричні показники щільності зв’язку, тобто такі, які не потребують визначення параметрів розподілу.