4. Середня та дисперсія альтернативної ознаки

Серед ознак, що вивчаються статистикою, є такі, які одним одиницям сукупності притаманні, а іншим – ні. Це, наприклад, вчений ступінь викладачів ВНЗів, диплом з відзнакою у випускників ВНЗ, отримання стипендії студентами, відповідність виготовленої продукції стандартам тощо. Як вже відзначалось⁵⁹, ознаки, якими володіють одні одиниці та не володіють інші, звуться альтернативними.

Розрахунок узагальнюючих показників (середньої та дисперсії) для альтернативної ознаки потребує прийняття певних умовних позначень. Звичайно припускається, що кількісне значення цієї ознаки становить “1” у тих одиниць сукупності, яким притаманна ця ознака, та дорівнює “0” для тих одиниць сукупності, які нею не володіють.

Виходячи з визначення сутності самої альтернативної ознаки, сукупність за нею поділяється лише на дві частини. Частка одиниць, що мають цю ознаку, звичайно позначається літерою “р”, а частка іншої частини сукупності, тобто тих її одиниць, що не мають альтернативної ознаки, позначається літерою “q”. Як відомо, сума усіх часток (у даному випадку їх лише дві) дорівнює 1 (або 100%). З цього виходить, що: р + q = 1 (або 100%); р = 1 – q; q = 1 – р.

Тепер, коли взято усі необхідні умовні позначки, звернемося до розрахунків шуканих узагальнюючих показників за відомими формулами (9, 24).

Середня альтернативної ознаки:

==. (31)

Тобто середня альтернативної ознаки завжди дорівнює частці тих одиниць сукупності, які володіють цією ознакою.

Дисперсія альтернативної ознаки: . (32)

Таким чином, дисперсія альтернативної ознаки завжди дорівнює добутку частки цієї ознаки на число, що доповнює цю частку до одиниці.

Слід розуміти, оскільки (p+q) не може перевищити одиницю, то дисперсія (pq) не може бути більшою за 0,25.

Добування кореня другого ступеня з дисперсії дає змогу отримати середнє квадратичне відхилення, тобто:

. (33)

Припустимо, за даними, що наведені у табл. 5.1, треба визначити частку тих облігацій, номінальна доходність яких не перевищує 24%. З цього виходить, що уся сукупність облігацій розпадається на дві частини за альтернативною ознакою: це облігації, номінальна доходність яких не перевищує 24%, та всі інші, номінальна доходність яких дорівнює 24% і більше. Для обчислення частки одиниць сукупності (облігацій), яким притаманна альтернативна ознака, знайдемо відношення кількості саме цих облігацій (75 шт.) до загальної їх кількості (500 шт.): або 15,0%. З цього виходить, що = 85% (100 -15) або 0,85.

Отже, дисперсія альтернативної ознаки буде дорівнювати:

,

а середнє квадратичне відхилення становитиме: .

Питання для самоперевірки і закріплення знань

1. Який ряд розподілу зветься варіаційним ?

2. Чим відрізняються дискретні та інтервальні варіаційні ряди ?

3. Чому розрахунок середнього значення ознаки, за якою побудовано варіаційний ряд, завжди здійснюється за формулою

середньої арифметичної зваженої ?

4. Що таке статистична мода ?

5. У яких випадках мода має перевагу перед середньою

величиною ?

6. Що можна встановити за допомогою медіани ?

7. Що таке варіація ознаки ?

8. На що вказує розмах варіації ?

9. Які обставини обумовлюють використання простого та

зваженого середнього лінійного відхилення ?

10. Які два показники варіації збігаються за змістом ?

11. У чому полягає значення дисперсії у статистиці?

12. Про що говорить “правило складання дисперсій”?

13. Чому дорівнює середня альтернативної ознаки ?

14. Вище якого значення не може піднятися дисперсія альтернативної ознаки ?

ВИБІРКОВЕ СПОСТЕРЕЖЕННЯ

1. ЗАГАЛЬНІ ВІДОМОСТІ

Під час знайомства з першим етапом статистичного дослідження – статистичним спостереженням – вже було наведено загальне визначення вибіркового спостереження. Але беручи до уваги, що вибіркове спостереження є найбільш науково обгрунтованим видом несуцільного спостереження, а тому досить часто використовуваним на практиці, розглянемо докладніше його значення, умови використання та методику проведення.

До вибіркового спостереження слід удаватися, коли суцільне:

• неекономічне (вимагає значних витрат коштів або часу);

• утруднене (поточна статистична звітність не дає достатнього для дослідника кола показників);

• неможливе (перевірка якості продукції іноді сполучається з псуванням або знищенням продукції).

Крім того, вибірковий метод може використовуватися для перевірки даних, які отримано під час суцільного спостереження.

Наприклад, проводячи перепис населення, збирають відомості про усіх жителів країни за обов’язковою програмою, що містить 13 запитань про важливіші демографічні та соціально-економічні характеристики кожної особи. Але при цьому чверть населення опитується за більш широкою програмою, питання якої дозволяють отримати відомості про населення, що є важливими та актуальними на момент проведення перепису. Це може бути інформація про міграцію населення, народжуваність, стан житлового фонду країни тощо. Такий підхід до збору всебічної інформації про населення значно знижує час проведення перепису (а це означає підвищення якості отриманої інформації), а за підсумком дозволяє скоротити фінансові витрати.

Широко використовується вибіркове спостереження, коли потрібно поглибити вивчення окремих явищ, відомості про які у поточній статистичній звітності вельми обмежені – вибірково збираються дані про: втрати робочого часу, простої устаткування (у статистиці промисловості); мотиви скоєння убивств або засоби розкрадання (у правовій статистиці); бюджети сімей окремих груп населення (у статистиці рівня добробуту населення); ринкові ціни (у статистиці цін) тощо.

Перевірка якості електричних лампочок контролює час безперервного їх горіння (до перегорання); контроль якості продукції прядильного виробництва передбачає оцінку міцності нитки при навантаженні до її розриву. Цілком очевидно, що перевірка усієї партії виробленої продукції у подібних обставинах не припустима. З цього виходить, що у таких випадках стає можливим лише вибірковий контроль.

Як відомо, вивчення будь-якої статистичної сукупності потребує її характеристики за допомогою узагальнюючих показників. Проведення вибіркового спостереження стикається з необхідністю обчислення середніх значень кількісної ознаки, що варіює, або відносної величини, що дає узагальнюючу характеристику сукупності за альтернативною ознакою (через частку одиниць сукупності, яким притаманна ця ознака). Неможливість або ускладнення отримання значень цих показників за усією генеральною сукупністю змушує до проведення вибіркового спостереження.

Таким чином, вибіркове спостереження – це таке несуцільне спостереження, під час якого з усієї сукупності (генеральної – “N”) відбирається випадково (наприклад, за жеребкуванням) і підлягає безпосередньому обстеженню її частина (вибіркова сукупність – “n”), для якої обчислюються узагальнюючі характеристики (середня – і частка альтернативної ознаки –), після чого отримані значення узагальнюючих вибіркових характеристик розповсюджуються з певною імовірністю (Р), що задається самим дослідником, на генеральну сукупність для отримання уявлення про узагальнюючі характеристики усієї сукупності (середньої –та частки –).

Спробуємо наведене визначення, що відбиває зміст та послідовність проведення розрахунків, відобразити схематично:

N ? ( , ) ( Р )

n ( , )

Рис. 6.1. Послідовність проведення розрахунків

у вибірковому спостереженні.

Отже, завдання вибіркового спостереження – отримати узагальнюючі показники усієї генеральної сукупності, не удаючись до суцільного спостереження, тобто за допомогою і дати вірне уявлення про і .

Відбір одиниць генеральної сукупності може здійснюватися кількома способами. Це власне випадкова вибірка, механічна вибірка, типова (районована) вибірка, серійна (гніздова) вибірка. Дамо стислу характеристику кожному способу відбору.

Власне випадкова вибірка застосовується за умов, коли між одиницями досліджуваної сукупності немає значних відмінностей (сукупність однорідна). Відбір одиниць з генеральної сукупності здійснюється шляхом жеребкування або за допомогою таблиці випадкових чисел.

Механічна вибірка передбачає послідовний відбір одиниць через рівні проміжки у генеральній сукупності (кожна п’ята, десята, сота тощо).

Типова (районована) вибірка застосовується у разі неоднорідності одиниць генеральної сукупності, при цьому сукупність спочатку поділяють на однорідні (типові) групи. Відбір одиниць може здійснюватися пропорційно обсягу типових груп або пропорційно груповій диференціації ознаки.

Серійна (гніздова) вибірка здійснюється через відбір (випадково або способом механічної вибірки) одиниць цілими групами (серіями, гніздами). Після цього у межах цих груп обстежують всі одиниці.

Слід пам’ятати, що головна умова утворення вибіркової сукупності – це випадковість. Отже, яким би способом не здійснювався відбір, в усіх випадках він повинен бути не упередженим, щоб не отримати помилкові результати. Випадковий відбір може здійснюватися як повторний і безповторний.

Повторна вибірка передбачає, що кожна відібрана з генеральної сукупності одиниця знову повертається до неї після обстеження. З цього виходить, що не виключена можливість повторного відбору та обстеження окремих одиниць.

Безповторна вибірка передбачає, що кожна відібрана одиниця виключається з числа одиниць генеральної сукупності, а це означає, що вона може потрапити у вибірку лише один раз.

Ці обставини враховуються при обчисленні помилок, які неминучі у вибірковому спостереженні.

2. ПОМИЛКИ ВИБІРКИ

Виходячи з самої природи несуцільного спостереження, усяке вибіркове спостереження неминуче стикається з помилками, які ще звуться помилками репрезентативності. Вони установлюють можливі межі відхилень вибіркових характеристик – середньої та частки від середньої та частки в генеральній сукупності.

За своєю природою помилки вибірки можуть бути тенденційними та випадковими. Виникнення тенденційних помилок пов’язане з навмисним порушенням вимоги випадковості під час утворення вибіркової сукупності (скажімо, відібрані гірші або найкращі одиниці сукупності). Тенденційні помилки призводять до того, що вибіркове спостереження втрачає свій сенс, оскільки за його показниками не можна правильно судити про показники усієї генеральної сукупності. Тому слід завжди пам’ятати головний організаційний принцип вибіркового спостереження – точно забезпечити додержання випадковості відбору. Помилки вибірки, що все ж таки виникають при дотриманні цього принципу, мають випадковий характер, тобто вони мають рівну можливість в однаковій мірі як применшити, так і перебільшити характеристики генеральної сукупності.

Закономірності змін випадкових помилок вибірки вивчає теорія імовірності та встановлює закон великих чисел, який доводить, що при збільшенні чисельності вибірки величина випадкової помилки зменшується, тобто між обсягом вибіркової сукупності та помилками, що виникають при дотриманні принципу випадковості відбору, існує обернена залежність. У той же час є чинник, який прямолінійно впливає на розмір помилки вибірки. Це варіація ознаки. Тобто при одному розмірі вибіркової сукупності буде утворюватися тим більша помилка, чим більшою буде варіація ознаки і навпаки – зменшення варіації призводитиме до скорочення помилки вибірки. Наведена залежність може бути показана співвідношенням:

.

На даній залежності грунтуються розрахунки середніх помилок вибірки () для усіх організаційних способів відбору.

Виходячи з призначення даного посібника, наведемо формули середніх помилок вибірки (середньої та частки) для найбільш розповсюджених видів відбору, а саме: власне випадкового та механічного⁶⁰.

Середня помилка вибірки ():

• при повторній вибірці:

для середньої – , (34)

для частки альтернативної ознаки – ; (35)

• при безповторній вибірці:

для середньої – , (36)

для частки альтернативної ознаки – .(37)

Те, що генеральна середня (або частка) не вийде за певні межі відносно вибіркових характеристик, можна стверджувати не з абсолютною достовірністю, а лише з певною мірою імовірності. Ця величина можливих відхилень вибіркових характеристик (середньої – та частки – ) від генеральних (середньої – і частки – ) зветься граничною помилкою вибірки.

Гранична помилка вибірки () у ”t” разів більша за середню помилку (форм. 38). Коефіцієнт кратності середньої помилки ”t” зветься ще коефіцієнтом довіри. Його величина залежить від імовірності, з якою можна гарантувати, що гранична помилка не перевищить t-кратну середню помилку.

Частіше за все беруться такі значення коефіцієнту t:

• t = 1 для імовірності Р = 0,683;

• t = 2 для імовірності Р = 0,954;

• t = 3 для імовірності Р = 0,997.

Таким чином, між середньою та граничною помилками (як для середньої, так і для частки) існує такий зв’язок:

= t · . (38)

Для визначення меж, у яких будуть знаходитися генеральна середня та генеральна частка альтернативної ознаки, використовують такі залежності (їх доводять у теорії імовірності – теорема Ляпунова):

│-│≤, або = ± , значить: - ≤ ≤ +; (39)

│-│≤ , або=± , значить:-≤≤+. (40)

Підсумовуючи розглянутий матеріал, ще раз відстежимо черговість проведення розрахунків при вибірковому спостереженні.

Якщо йдеться про отримання середнього значення кількісної ознаки у генеральній сукупності (), то визначається його розмір у вибірковій сукупності (). Далі також за вибірковими даними обчислюється показник варіації цієї ознаки () і середня помилка вибірки (). Потім задається бажана імовірність отримання результатів (Р) і відносно неї визначається величина коефіцієнту довіри (t), завдяки якій обчислюється гранична помилка (). Останню слід відняти від вибіркової середньої та додати до неї (±). Отримані величини є тими межами, у яких буде знаходитися генеральна середня. Описана черговість розрахунків може бути зображена схематично (рис. 6.2).

Якщо йдеться про частку одиниць генеральної сукупності (), яким притаманна альтернативна ознака, то перш за все визначається така частка у вибірковій сукупності (). Це дає змогу відразу обчислити середню помилку вибірки для частки (). Подальші дії дублюють вищенаведені: відносно імовірності, що задається дослідником (P), встановлюється величина коефіцієнта довіри (t) та розраховується гранична помилка для частки ().

–? ±

Р t

Рис. 6.2. Черговість розрахунків середнього значення кількісної ознаки у генеральній сукупності.

Вона також віднімається та додається (±) до вибіркової частки, що дозволяє отримати межі коливання цієї частки у генеральній сукупності. Схематично ця черговість має вигляд (рис. 6.3):

–? ±

P t

Рис. 6.3. Черговість розрахунків частки одиниць з альтернативною ознакою у генеральній сукупності.

Розглянемо приклади для ілюстрації методики розрахунків за різновидом власне випадкової вибірки – механічним відбором.

Припустимо, що вибіркове обстеження продажу облігацій на аукціоні (табл. 5.1.) охоплює 2% усіх проданих облігацій. Тобто, саме ті 500 облігацій, відомості про які наведено у таблиці, створюють вибіркову сукупність. А з означеного припущення виходить, що уся генеральна сукупність складається з 25000 облігацій ((500 : 2%) · 100% або (500:0,02)).

Аналіз результатів аукціону потребує :

а) встановити межі коливання середньої номінальної доходності облігацій в усій генеральній сукупності;

б) виявити частку облігацій, які продано з номінальною доходністю не нижче 32%, та межі її коливання у генеральній сукупності.

Імовірність для розрахунку середньої нехай становить 0,954 (а це означає, що t = 2); а імовірність, з якою знайдемо межі коливання шуканої частки у генеральній сукупності, підвищимо до 0,997 (тобто t у розрахунках буде дорівнювати “3”).

Як відомо, усяка механічна вибірка є безповторною. Тому для розрахунків середніх помилок скористаємося формулами (36) та (37).

а) Приймемо до уваги результати проведених раніше розрахунків за даними табл. 5.1. – середньої (с.62) та дисперсії (с.74). Маючи ці дані, обчислимо середню помилку вибірки для середньої номінальної доходності – :

= = = ± 0,18%.

Виходячи з прийнятої імовірності та табличного значення коефіцієнта довіри, знайдемо граничну помилку вибірки – :

= t · = 2 · (± 0,18%) = ± 0,36%.

Таким чином, генеральна середня становить:

= ± = 28,52% ± 0,36%.

А це означає, що:

28,52 – 0,36 ≤ ≤ 28,52 + 0,36 або 28,16 ≤ ≤ 28,88.

Висновок: з імовірністю 0,954 можна стверджувати, що середня номінальна доходність усіх проданих на аукціоні облігацій не вийде за межі від 28,16 до 28,88%.

б) З усіх облігацій, що обстежувалися, 135 шт. мали номінальну доходність не нижче 32% . Це означає, що частка цих облігацій у вибірковій сукупності () становила: = 135 : 500 = 0,27 або 27%.

Середня помилка вибірки для частки ( ) буде дорівнювати:

=== ± 0,02 або ±2,0%.

Гранична помилка вибірки для частки ( ) становитиме:

= t · = 3 · (± 0,02) = ± 0,06 або ±6,0%.

Отже, частка облігацій, номінальна доходність яких була не нижча за 32%, угенеральній сукупності дорівнює:

= ± = 27% ± 6%, а це означає, що:

27% - 6% ≤ ≤ 27% + 6% або 21% ≤ ≤ 33% .

Висновок:з імовірністю 0,997 можна стверджувати, що частка облігацій з номінальною доходністю 32% і більше в генеральній сукупності не вийде за межі від 21 до 33%.

3. ВИЗНАЧЕННЯ НЕОБХІДНОЇ ЧИСЕЛЬНОСТІ ВИБІРКИ

Під час проведення вибіркового спостереження виникає питання про те, якою повинна бути вибірка за чисельністю, тобто чому дорівнюватиме “n”. Надмірна чисельність вибірки призведе до затягнення строків дослідження, зайвих витрат часу і коштів, а недостатня ж дасть результати з великою помилкою репрезентативності. Це питання можна вирішити лише за умови, коли точність розрахунків задаватиметься заздалегідь. Тобто наперед свідомо задається помилка вибірки, після чого величина “n” виводиться з формул потрібної граничної помилки (при повторному чи безповторному відборі, як для середньої, так і для частки). Ці перетворення дозволяють отримати відповідні формули для визначення чисельності вибіркової сукупності.

Необхідна чисельність випадкової повторної вибірки:

– при визначенні середньої: ; (41)

– при визначенні частки: . (42)

Необхідна чисельність випадкової безповторної вибірки:

– при визначенні середньої: ; (43)

– при визначенні частки: . (44)

Подібні завдання зустрічаються і аналогічно вирішуються для усіх способів відбору⁶¹. Проілюструємо використання наведених формул на прикладі.

Поставимо питання за умовами розглянутого вище прикладу:

а) скільки треба було відібрати облігацій (n) з усіх проданих на аукціоні (N), щоб визначити їх середню номінальну доходність з точністю, наприклад, до 0,5% ( = 0,5%), при цьому впевненість у цій точності – 0,954? Виходячи з інших аналогічних обстежень, дисперсія дорівнюватиме 20.

Маємо: :

Це означає, що за умовами призначеної точності розрахунків, для отримання шуканих відомостей про середню номінальну доходність облігацій достатньо відібрати та обстежити 316 облігацій з усіх проданих на аукціоні.

б) скільки слід відібрати облігацій, щоб визначити частку тих, що мають номінальну доходність не нижче 32% з точністю, наприклад, до 4% (= 4% або 0,04)? Візьмемо імовірність 0,997, а дисперсія нехай становить 0,25, тобто дорівнює максимальному її значенню для альтернативної ознаки (див. стор.79).

Маємо:

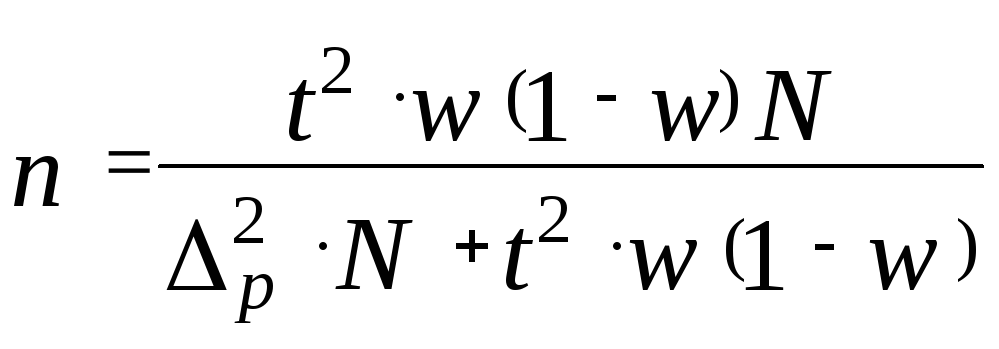
Це означає, що за умовами призначеної точності розрахунків, для отримання шуканої частки облігацій слід вже відібрати з генеральної сукупності не менш ніж 1330 облігацій.

Питання для самоперевірки і закріплення знань

1. Що таке вибіркове спостереження?

2. Коли слід удаватися до вибіркового спостереження?

3. В чому полягає головне завдання вибіркового спостереження?

4. Якими способами може здійснюватися відбір одиниць для

вибіркової сукупності?

5. Що таке повторна і безповторна вибірка?

6. Які відрізняють помилки вибірки за їх природою?

7. В чому полягає головний організаційний принцип вибіркового спостереження?

8. На співвідношенні яких показників грунтуються розрахунки

середніх помилок вибірки?

9. Яка залежність існує між середньою та граничною помилками вибірки?

10. Які залежності, що доводяться у теорії імовірності, використовують для визначення меж коливання середньої та частки у генеральній сукупності?

11. Наведіть схематично черговість проведення розрахунків при вибірковому спостереженні.

12. Як вирішується питання визначення необхідної чисельності вибірки?

СТАТИСТИЧНІ МЕТОДИ ВИВЧЕННЯ ВЗАЄМОЗВ’ЯЗКІВ

1. ЗАГАЛЬНІ ВІДОМОСТІ ПРО ВЗАЄМОЗВ’ЯЗКИ

Усі явища та процеси, що існують у природі та суспільстві, пов’язані між собою, залежать одне від одного, безперервно змінюються і одне одного зумовлюють . Тому вивчення взаємозв’язків та причинних залежностей є найважливішим завданням статистики, яка дає числові вираження закономірностей суспільного розвитку. Причинна залежність виступає головною формою закономірностей зв’язків; при цьому причина сама по собі не визначає повною мірою наслідків. Останні часом суттєво залежать також від умов, у яких діє ця причина. Отже, як умови, так і причини являють собою чинники суспільного розвитку. Ознаки, що характеризують чинники (фактори), називаються факторними, а ознаки, які характеризують наслідок дій цих факторів, – результативними.

За напрямком зв’язки бувають прямі і обернені.

Прямізв’язки – це такі, коли зростання (або зниження) факторної ознаки призводить також до зростання (або зниження) результативної ознаки. Це можна представити такою схемою: Х і Y , або Х і Y .

Наприклад, підвищення рівня механізації праці веде до зростання продуктивності праці, збільшення чисельності автотранспорту викликає підвищення кількості дорожньо-транспортних випадків, зменшення кількості опадів призводить до зниження врожайності сільськогосподарських культур тощо.

Обернені зв’язки – це такі, коли зростання (або зниження) факторної ознаки призводить, навпаки, до зниження (або зростання) результативної ознаки . Представимо їх також схематично : Х , а Y , або Х , а Y .

Наприклад, зростання продуктивності праці може призвести до зниження собівартості продукції, скорочення термінів проведення перепису населення дає змогу підвищити точність отриманих матеріалів, зростання цін викликає зменшення споживання окремих товарів тощо.

За характером залежностей між факторними та результативними ознаками розрізняють функціональні та стохастичні (імовірнісні) зв’язки.

Функціональні зв’язки називають також точними або повними і вони відбивають безпосередні залежності між кожним значенням факторної та відповідним значенням результативної ознаки. Іншими словами, кожному значенню факторної ознаки відповідає тільки одне значення результативної ознаки. Цю залежність можна виразити схематично (рис. 7.1):

… …

Рис. 7.1. Схематичне зображення функціонального зв’язку.

Прикладом функціональних залежностей можуть бути перш за все математичні й фізичні залежності. Так, зміна довжини сторони квадрату в 2 рази призведе до зміни площі цієї фігури у 4 рази; якщо швидкість руху впаде наполовину (тобто знизиться в 2 рази), то за той самий час буде пройдено у два рази менший шлях. Зустрічаються функціональні залежності й при дослідженні суспільних явищ. Скажімо, обсяг виробленої продукції можна виразити добутком чисельності робітників і продуктивності праці, середньомісячна продуктивність праці робітника є добутком середньогодинної продуктивності праці, середньої тривалості робочого дня та середньої тривалості робочого місяця. Співмножники цих залежностей є факторами, що пропорційно впливають на результат-добуток, тобто на показник-функцію. Такі залежності з кола суспільних явищ вивчаються, а оцінка впливу кожного показника-фактора на результативний показник-функцію здійснюється за допомогою індексного методу⁶².

Слід також зазначити, що функціональні зв’язки між економічними показниками можна відстежувати за допомогою балансового методу. Так, залишок товарів на складі на кінець звітного періоду повністю залежить від такого залишку на початок періоду та надходження і продажу товарів протягом цього періоду. За усіма цими даними складається баланс руху товарів у звітному періоді.

Стохастичні зв’язки називають ще випадковими і неповними, оскільки кожному значенню факторної ознаки відповідає кілька значень результативної. Це також можна представити схематично (рис. 7.2).

Різновидом стохастичного зв’язку є кореляційний зв’язок, при якому кожному значенню або групі значень факторної ознаки () відповідає середнє значення результативної ознаки (), в той час як в кожному окремому випадку результативна ознака () може мати безліч різних значень.

… …

Рис. 7.2. Схематичне зображення стохастичного зв’язку.

Скажімо, очевидно, що є зв’язок між продуктивністю праці та рівнем її механізації або прийнятої системи оплати праці, між рівнем споживання товарів та рівнем середньодушового доходу, між числом дорожньо-транспортних випадків та споживанням алкоголю тощо. Але усі перераховані та їм подібні залежності випадкові та неповні, оскільки названі результативні ознаки залежать не лише від наведених факторних ознак, а кожна з перерахованих факторних ознак впливає не лише на ту результативну ознаку, що названо. Так, продуктивність праці перебуває під впливом значно більшого кола чинників. Це і якість заготовки, і рівень кваліфікації робітника, і навіть його настрій та самопочуття тощо. З цього виходить, що один і той самий рівень продуктивності праці можуть мати робітники з різним рівнем показника-фактора і, навпаки, кілька робітників можуть мати, наприклад, однаковий рівень механізації своєї праці, але виконувати роботу з різною продуктивністю. У цих випадках може йтися лише про середні зміни результативної ознаки у залежності від змін середнього значення ознаки факторної, тобто про кореляційну залежність.

Існують багаточисельні засоби та прийоми встановлення наявності, напрямку та тісноти зв’язку між показниками. Так, при викладі методики проведення групування статистичних матеріалів було надано характеристику такому його виду, як аналітичне групування⁶³. Нагадаємо, що аналітичне групування дає змогу відповісти на питання про наявність і напрямок зв’язку. Але з його допомогою не можна оцінити тісноту зв’язку. В той же час достоїнством аналітичного групування є можливість його використання в усіх випадках незалежно від змісту факторної (групованої) ознаки, тобто вона може бути як атрибутивною, так і кількісною, бо за кожною з них можна проводити групування. Отримання ж чисельної характеристики тісноти зв’язку потребує продовження роботи з аналітичним групуванням і проведення на його основі дисперсійного аналізу.