Теорема Гюйгенса-Штейнера

Найдем связь между моментами инерции относительно двух различных параллельных осей. Она устанавливается теоремой Гюйгенса-Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела относительно оси проходящей через центр масс, параллельно данной и произведения массы на квадрат расстояния между осями.

Докажем эту теорему. Пусть S сечение тела. Будем предполагать, что центр масс находится в точке О и оси, проходящие через точки О и А, перпендикулярны к рисунку. Мысленно разобьем тело на элементарные массы . Момент инерции тела найдем, проинтегрировав по всем элементарным массам. Радиус-вектор элементарной массы относительно оси А , где - ее радиус-вектор относительно оси О, - радиус-вектор , его модуль равен расстоянию между осями. Таким образом

. (5.11)

Умножая обе части равенства (5.11) на и интегрируя по всему объему, получим:

. (5.12)

Так как ось О проходит через центр масс, последний интеграл в (5.12) обращается в нуль.

.

Интеграл слева дает момент инерции относительно оси А, первый интеграл справа - момент инерции относительно оси О, второй интеграл справа дает полную массу тела. Откуда

. (5.13)

Это и есть аналитическое выражение теоремы Гюйгенса-Штейнера.

Примеры вычисления моментов инерции

1. Определим момент инерции тонкого однородного стержня длиною L и массой m относительно оси, проходящей через один из его концов. (см.рис.)

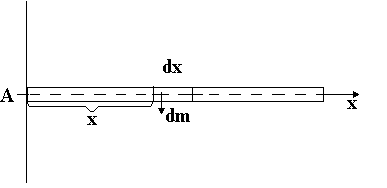
Направим ось Х вдоль стержня. Стержень будем считать тонким. Выделим элементарную массу , имеющую длинуи расположенную на расстоянии Х от оси вращения. Причем, поскольку стержень однородный масса этого элемента

Тогда

Проинтегрировав по всей длине стержня получим:

Момент инерции этого же стержня относительно оси, проходящей через центр масс определяется как:

2. Определим момент инерции однородного диска, расположенного

перпендикулярно оси вращения, проходящей через центр масс. Радиус диска R, масса – m. Используя симметрию задачи, разобьем диск на элементарные массы в виде тонких колец радиусом r и шириной . (см.рис.)

Масса этого элемента , где- площадь поперечного сечения диска или поверхностная плотность диска,- площадь кольца. Тогда. Интегрируя в пределах от 0 доR, получим:

3. Тонкое однородное кольцо, расположенное перпендикулярно оси вращения, проходящей через центр масс. (см.рис.)

Выделим элементарную массу , длиной, тогда, здесь- линейная плотность массы, то есть масса

приходящаяся на единицу длины. Так как все элементарные массы расположены на одинаковом расстоянии от оси вращения (кольцо тонкое)